Cho phương trình \left(log\right)_{9} x^{2} - \left(log\right)_{3} \left(\right. 6 x - 1 \right) = - \left(log\right)_{3} m (m là tham số thực ). Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm ?

A.  

$6 .$

B.  

vô số.

C.  

$5 .$

D.  

$7 .$

Đáp án đúng là: C

(VD):
Phương pháp:
Biến đổi phương trình về dạng $\left(\text{log}\right)_{3} a = \left(\text{log}\right)_{3} b$
Cách giải:
$\left(\text{log}\right)_{9} x^{2} - \left(\text{log}\right)_{3} \left( 6 x - 1 \right) = - \left(\text{log}\right)_{3} m$
Đk: $x > \dfrac{1}{6} , m > 0$
$\Leftrightarrow \left(\text{log}\right)_{3^{2}} x^{2} - \left(\text{log}\right)_{3} \left( 6 x - 1 \right) = - \left(\text{log}\right)_{3} m$
$\Leftrightarrow \left(\text{log}\right)_{3} x + \left(\text{log}\right)_{3} m = \left(\text{log}\right)_{3} \left( 6 x - 1 \right)$
$\Leftrightarrow \left(\text{log}\right)_{3} \left( m x \right) = \left(\text{log}\right)_{3} \left( 6 x - 1 \right)$
$\Leftrightarrow m x = 6 x - 1$
$\Leftrightarrow m = \dfrac{6 x - 1}{x} \left( \text{do}\&\text{nbsp}; x > \dfrac{1}{6} \Rightarrow x \neq 0 \right)$
Xét $f \left( x \right) = \dfrac{6 x - 1}{x} \Rightarrow f^{'} \left( x \right) = \dfrac{1}{x^{2}} > 0$

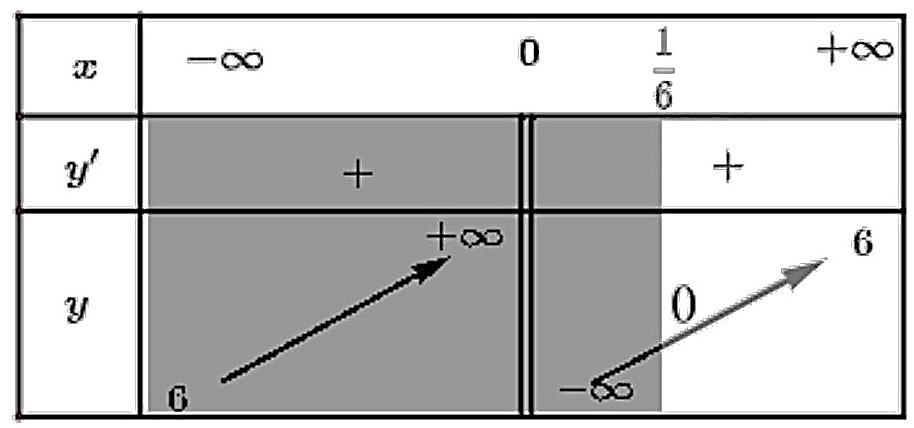
Từ BBT suy ra phương trình có nghiệm khi $0 < m < 6 \Rightarrow m \in \left{ 1 , 2 , 3 , 4 , 5 \right}$
Vậy có 5 giá trị m nguyên thỏa mãn