Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và $A B = 6 a , A C = 9 a , A D = 3 a$. Gọi M, N, P lần lượt là trọng tâm của các tam giác ABC, ACD, ADB. Tính thể tích V của khối tứ diện AMNP.

Cho tứ diện

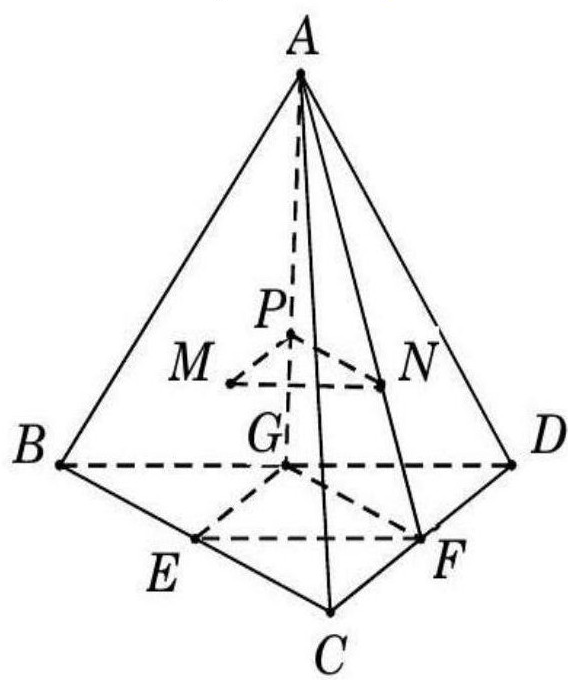
Cho tứ diện $A B C D$ có $A B = C D = 2 a$. Gọi $M$, $N$ lần lượt là trung điểm $A D$và $B C$. Biết $M N = a \sqrt{3}$, góc giữa hai đường thẳng $A B$ và $C D$ bằng.

Cho tứ diện $A B C D$ có $A D \bot \left( A B C \right)$, $A C = A D = 2$, $A B = 1$ và $B C = \sqrt{5}$. Tính khoảng cách $d$ từ $A$ đến mặt phẳng $\left( B C D \right)$.

Cho tứ diện $A B C D$ có tam giác $B C D$ vuông tại $C$, $A B$ vuông góc với mặt phẳng $\left( B C D \right)$, $A B = 5 a \textrm{ } , \textrm{ } B C = 3 a$ và $C D = 4 a$. Tính bán kính $R$ của mặt cầu ngoại tiếp tứ diện $A B C D$.

Trong không gian với hệ toạ độ $O x y z$, cho tứ diện $A B C D$ với $A \left( 1 \textrm{ } ; \textrm{ } - 4 \textrm{ } ; \textrm{ } 2 \right)$, $B \left( 2 \textrm{ } ; \textrm{ } 1 \textrm{ } ; \textrm{ } - 3 \right)$, $C \left( 3 \textrm{ } ; \textrm{ } 0 \textrm{ } ; \textrm{ } - 2 \right)$, $D \left( 2 \textrm{ } ; \textrm{ } - 5 \textrm{ } ; \textrm{ } - 1 \right)$. Điểm $G$ thoả mãn $\overset{\rightarrow}{G A} + \overset{\rightarrow}{G B} + \overset{\rightarrow}{G C} + \overset{\rightarrow}{G D} = \overset{\rightarrow}{0}$ có toạ độ là

Trong không gian với hệ trục tọa độ $O x y z$. Cho tứ diện $A B C D$ có điểm $A \left( 1 ; - 2 ; 3 \right)$, $B \left( 5 ; 0 ; - 1 \right)$, $C \left( - 1 ; 2 ; 0 \right)$, $D \left( 0 ; 3 ; 4 \right)$. Trên các cạnh $A B$, $A C$, $A D$ lần lượt lấy các điểm $M$, $N$, $P$ thỏa $\dfrac{A B}{A M} + \dfrac{A C}{A N} + \dfrac{A D}{A P} = 9$ và có thể tích $A M N P$ nhỏ nhất. Khi đó mặt phẳng $\left( M N P \right)$ đi qua điểm nào sau đây?

Trong không gian với hệ trục tọa độ $O x y z$, cho tứ diện $A B C D$ có điểm $A \left( 1 ; 1 ; 1 \right)$, $B \left( 2 ; 0 ; 2 \right)$, $C \left( - 1 ; - 1 ; 0 \right)$, $D \left( 0 ; 3 ; 4 \right)$. Mặt phẳng $\left( \alpha \right)$ cắt các cạnh $A B , A C , A D$ lần lượt tại các điểm $B^{'} , C^{'} , D^{'}$ thỏa mãn $\dfrac{A B}{A B^{'}} + \dfrac{A C}{A C^{'}} + \dfrac{A D}{A D^{'}} = 4$. Biết tứ diện $A B^{'} C^{'} D^{'}$ có thể tích nhỏ nhất. Mặt phẳng $\left( \alpha \right)$ cắt trục hoành tại điểm $M \left( \dfrac{a}{b} ; 0 ; 0 \right) \left( a , b \in \mathbb{Z} ; b \neq 0 \right)$, $\dfrac{a}{b}$ là phân số tối giản. Tính $a b$.

Đặt một điện áp xoay chiều ổn định u=U√2cosωt vào hai đầu đoạn mạch có R,L,C nối tiếp mà tụ điện có điện dung thay đổi được. Mắc lần lượt các vôn kế V₁, V₂ ,V₃ có điện trở vô cùng lớn vào hai đầu điện trở thuần hai đầu cuộn cảm và giữa hai bản của tụ điện. Điều chỉnh điện dung của tụ điện sao cho số chỉ của vôn kế V₁ ,V₂ ,V₃ lần lượt chỉ giá trị lớn nhất và người ta thấy: số chỉ lớn nhất của V₃ bằng 3 lần số chỉ lớn nhất của V₂. Tỉ số giữa chỉ số lớn nhất của V₃ so với số chỉ lớn nhất của V₁ là: