Cho tứ diện
có
. Gọi
,
lần lượt là trung điểm
và
. Biết
, góc giữa hai đường thẳng
và
bằng.
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: C
Cho tứ diện có . Gọi , lần lượt là trung điểm và . Biết , góc giữa hai đường thẳng và bằng.
.
.
.
.
Đáp án đúng là: C
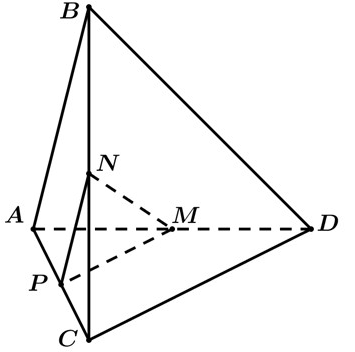
Gọi là trung điểm , ta có và , suy ra .
Dễ thấy .
Xét ta có
.
Câu hỏi tương tự:
#7898 THPT Quốc giaToán
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và . Gọi M, N, P lần lượt là trọng tâm của các tam giác ABC, ACD, ADB. Tính thể tích V của khối tứ diện AMNP.
Lượt xem: 134,362 Cập nhật lúc: 15:16 17/05/2025
#7567 THPT Quốc giaToán
Cho hàm số có đồ thị . Gọi , là hai điểm thuộc hai nhánh của và các tuyến tiếp của tại , cắt các đường tiệm cận ngang và đứng của lần lượt tại các điểm , , , . Diện tích tứ giác có giá trị nhỏ nhất bằng?
Lượt xem: 128,759 Cập nhật lúc: 19:18 15/05/2025
#2290 THPT Quốc giaVật lý
Điện năng được truyền từ đường dây điện một pha có điện áp hiệu dụng ổn định 220V vào nhà một hộ dân bằng đường dây tải điện có chất lượng kém. Trong nhà của hộ dân này, dùng một máy biến áp lí tưởng để duy trì điện áp hiệu dụng ở hai đầu ra luôn là 220V (gọi là máy ổn áp). Máy ổn áp này chỉ hoạt động khi điện áp hiệu dụng ở đầu vào lớn hơn 110V. Tính toán cho thấy, nếu công suất sử dụng điện trong nhà là 1,8 kW thì tỉ số giữa điện áp hiệu dụng ở đầu ra và điện áp hiệu dụng ở đầu vào (tỉ số tăng áp) của máy ổn áp là 1,2. Coi điện áp và cường độ dòng điện luôn cùng pha. Nếu công suất sử dụng điện trong nhà là 2,4kW thì tỉ số tăng áp của máy ổn áp là
Lượt xem: 39,046 Cập nhật lúc: 14:49 17/05/2025
#11668 THPT Quốc giaVật lý
Cho hai dây dẫn thẳng, dài, đặt song song trong cùng một mặt phẳng như hình vẽ. Trong hai dây dẫn có hai dòng điện cùng chiều chạy qua. Gọi M là điểm mà tại đó cảm ứng từ tổng hợp bằng 0. M chỉ có thể nằm tại vùng
Lượt xem: 198,491 Cập nhật lúc: 15:29 17/05/2025
#8543 THPT Quốc giaToán
Cho tứ diện có tam giác vuông tại , vuông góc với mặt phẳng , và . Tính bán kính của mặt cầu ngoại tiếp tứ diện .
Lượt xem: 145,378 Cập nhật lúc: 22:47 12/05/2025
#7604 THPT Quốc giaToán
Cho tứ diện
có ba cạnh , , đôi một vuông góc và đều bằng . Tính thể tích tứ diện làLượt xem: 129,328 Cập nhật lúc: 20:16 17/05/2025
#8239 THPT Quốc giaToán
Cho tứ diện có , , và . Tính khoảng cách từ đến mặt phẳng .
Lượt xem: 140,120 Cập nhật lúc: 01:18 17/05/2025
#7728 THPT Quốc giaToán
Trong không gian với hệ trục tọa độ , cho tứ diện có điểm , , , . Mặt phẳng cắt các cạnh lần lượt tại các điểm thỏa mãn . Biết tứ diện có thể tích nhỏ nhất. Mặt phẳng cắt trục hoành tại điểm , là phân số tối giản. Tính .
Lượt xem: 131,587 Cập nhật lúc: 13:48 17/05/2025
#8209 THPT Quốc giaToán
Trong không gian với hệ trục tọa độ . Cho tứ diện có điểm , , , . Trên các cạnh , , lần lượt lấy các điểm , , thỏa và có thể tích nhỏ nhất. Khi đó mặt phẳng đi qua điểm nào sau đây?
Lượt xem: 139,666 Cập nhật lúc: 10:37 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 40 phút
5,379 xem400 thi
