Cho hình thang ABCD vuông tại A và D có
Tính thể tích V của khối tròn xoay sinh ra bởi hình thang ABCD khi quanh xung quanh đường thẳng BC.

A.
B.
C.
D.
Đáp án đúng là: C
Cho hình thang ABCD vuông tại A và D có
Tính thể tích V của khối tròn xoay sinh ra bởi hình thang ABCD khi quanh xung quanh đường thẳng BC.

Đáp án đúng là: C
Cho hình thang ABCD vuông tại A và D có
Tính thể tích V của khối tròn xoay sinh ra bởi hình thang ABCD khi quanh xung quanh đường thẳng BC.

A. B. C. D.
Lời giải
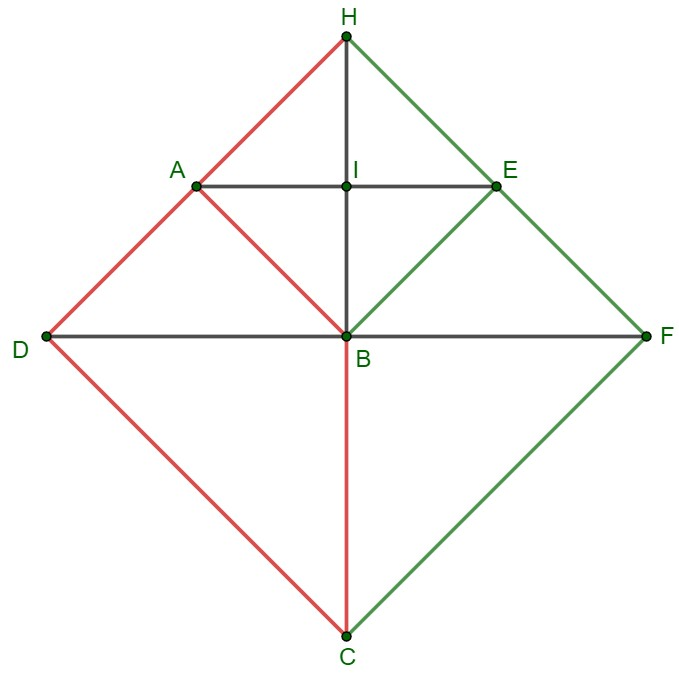
Thể tích khối tròn xoay sinh ra sau khi quay hình thang xung quanh cạnh được tính như sau: với là thể tích khối nón có đỉnh là có đáy là hình tròn tâm , là khối nón đỉnh có đáy là hình tròn tâm tâm
Tam giác vuông cân tại nên
Nên
Dễ dàng chứng minh được là hình vuông nên
Nên
Vậy
Câu hỏi tương tự:
#4809 THPT Quốc giaVật lý
Ở mặt nước có hai nguồn kết hợp đặt tại A và B, dao động cùng pha theo phương thẳng đứng, có bước sóng λ. Trên có 9 vị trí mà ở đó các phân tử nước dao động với biên độ cực đại. C và D là hai điểm ở mặt nước sao cho là hình vuông. M là một điểm thuộc cạnh và nằm trên vân cực đại giao thoa bậc nhất . Biết phần tử tại M dao động cùng pha với các nguồn. Độ dài đoạn gần giá trị nào nhất sau đây?
Lượt xem: 81,858 Cập nhật lúc: 15:37 17/05/2025
#3028 THPT Quốc giaVật lý
Ở mặt nước, hai nguồn sóng kết hợp đặt tại hai điểm và , dao động cùng pha theo phương thẳng đứng, phát ra hai sóng lan truyền có bước sóng . Hai điểm và ở mặt nước sao cho là hình vuông. Trên đoạn thẳng có 19 điểm cực đại giao thoa. Trên đoạn thẳng , gọi là điểm cực đại giao thoa gần nhất và là điểm cực đại giao thoa mà phần tử sóng tại và dao động cùng pha với nhau. Độ dài đoạn thẳng ngắn nhất gần với giá trị nào sau đây?
Lượt xem: 51,560 Cập nhật lúc: 15:59 17/05/2025
#2486 THPT Quốc giaVật lý
Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm A và B dao động cùng pha theo phương thẳng đứng, phát ra hai sóng lan truyền trên mặt nước với bước sóng λ. Ở mặt nước, C và D là hai điểm sao cho ABCD là hình vuông. Trên đoạn BC có 6 điểm cực đại giao thoa và 7 điểm cực tiểu giao thoa. Trên đoạn CD, điểm cực tiểu giao thoa đầu tiên (kể từ C) cách C một khoảng lớn nhất là
Lượt xem: 42,455 Cập nhật lúc: 06:17 14/05/2025
#2387 THPT Quốc giaVật lý
Ở trên mặt nước có hai nguồn sóng kết hợp đặt tại hai điểm A và B, dao động với cùng tần số, cùng biên độ và cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng λ. Cho biết AB=5,5λ. Ở mặt nước có đường thẳng song song với AB, trên lấy hai điểm C và D sao cho ABCD là hình chữ nhật. Hai điểm M,N theo thứ tự thuộc đoạn CD và CB, sao cho . Di chuyển theo phương vuông góc với cạnh AB đến vị trí sao cho góc MAN đạt giá trị lớn nhất, khi đó số điểm cực đại giao thoa trên đoạn MN bằng
Lượt xem: 40,685 Cập nhật lúc: 21:29 13/05/2025
#3914 THPT Quốc giaVật lý
Trong thí nghiệm giao thoa sóng trên mặt nước với hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng, phát hai sóng truyền trên mặt nước với bước sóng λ thì . Trên mặt nước có hai điểm sao cho là hình chữ nhật. Biết trên có 7 điểm cực đại giao thoa và tại là hai điểm cực tiểu giao thoa. Điểm cực đại giao thoa nằm trên và gần C nhất cách C đoạn gần bằng
Lượt xem: 66,711 Cập nhật lúc: 22:12 14/05/2025
#8277 THPT Quốc giaToán
Cho hình thang vuông tại và có , và với . Gọi , lần lượt là thể tích các khối tròn xoay tạo thành khi quay hình thang (kể cả các điểm trong) quanh đường thẳng và . Tìm để .
Lượt xem: 140,864 Cập nhật lúc: 20:17 17/05/2025
#7785 THPT Quốc giaToán
Cho hình chóp có đáy là hình thang , , . Biết rằng và . Cạnh bên hợp với đáy một góc . Gọi là góc giữa hai mặt phẳng và . Khẳng định nào dưới đây đúng?
Lượt xem: 132,527 Cập nhật lúc: 19:08 13/05/2025
#7721 THPT Quốc giaToán
Cho hình chóp có đáy là hình thang vuông tại và . Biết . Cạnh bên vuông góc với mặt phẳng và . Khoảng cách từ đến mặt phẳng bằng
Lượt xem: 131,419 Cập nhật lúc: 17:09 17/05/2025
#8635 THPT Quốc giaToán
Cho hình trụ có hai đáy là hình tròn tâm và , chiều cao . Mặt phẳng đi qua tâm và tạo với một góc , cắt hai đường tròn tâm và tại bốn điểm là bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng . Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
Lượt xem: 146,962 Cập nhật lúc: 14:16 14/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
324 xem9 thi
