Cho hình trụ có hai đáy là hình tròn tâm
và
, chiều cao
. Mặt phẳng đi qua tâm
và tạo với
một góc
, cắt hai đường tròn tâm
và
tại bốn điểm là bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng
. Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: B
Cho hình trụ có hai đáy là hình tròn tâm và , chiều cao . Mặt phẳng đi qua tâm và tạo với một góc , cắt hai đường tròn tâm và tại bốn điểm là bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng . Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
.
.
.
.
Đáp án đúng là: B
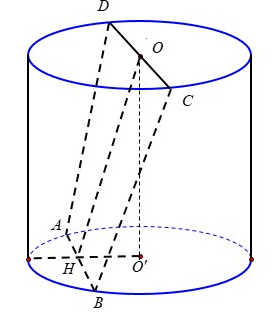
Ta có góc giữa mặt phẳng và là góc , .
Ta có
Theo giả thiết diện tích hình thang bằng nên ta có
Vậy thể tích khối trụ bằng .
Câu hỏi tương tự:
#8555 THPT Quốc giaToán
Cho hình trụ có hai đáy là hai hình tròn và ; là một dây cung của đường tròn sao cho tam giác đều và mặt phẳng tạo với mặt phẳng chứa đường tròn một góc . Tính thể tích của hình trụ đã cho.
Lượt xem: 145,544 Cập nhật lúc: 16:43 07/05/2025
#8353 THPT Quốc giaToán
Cho khối trụ có hai đáy lần lượt là hình tròn tâm và chiều cao bằng . Một mặt phẳng đi qua tâm , tạo với một góc đồng thời cắt hai đường tròn tâm tại bốn điểm tạo thành bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng . Thể tích của khối trụ đã cho bằng
Lượt xem: 142,108 Cập nhật lúc: 16:57 07/05/2025
#8740 THPT Quốc giaToán
Cho hình trụ có tâm hai đường tròn đáy lần lượt là và , bán kính đáy hình trụ bằng . Trên đường tròn đáy và lần lượt lấy hai điểm sao cho tạo với trục của hình trụ một góc và có khoảng cách đến trục của hình trụ bằng . Tính thể tíc khối chóp
Lượt xem: 148,658 Cập nhật lúc: 20:46 06/05/2025
#8426 THPT Quốc giaToán
Cho hình trụ có hai đáy là hai hình tròn và , thiết diện qua trục của hình trụ là hình vuông. Gọi và là hai điểm lần lượt nằm trên hai đường tròn và . Biết và khoảng cách giữa và bằng . Bán kính đáy của hình trụ bằng
Lượt xem: 143,349 Cập nhật lúc: 02:07 09/05/2025
#11393 THPT Quốc giaToán
Cho hình trụ có hai đáy là hai hình tròn và , thiết diện qua trục của hình trụ là hình vuông. Gọi và là hai điểm lần lượt nằm trên hai đường tròn và . Biết và khoảng cách giữa và bằng . Tính diện tích xung quanh của hình trụ.
Lượt xem: 193,756 Cập nhật lúc: 19:16 03/05/2025
#8387 THPT Quốc giaToán
Cho hình trụ có hai đáy là hai hình tròn và , chiều cao . Một mặt phẳng đi qua trung điểm của và tạo với một góc . Mặt phẳng cắt đường tròn đáy tại hai điểm . Tính độ dài đoạn thẳng theo ?
Lượt xem: 142,692 Cập nhật lúc: 10:11 09/05/2025
#7931 THPT Quốc giaToán
Cho hình hộp chữ nhật có . Tính diện tích toàn phần của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hai hình chữ nhật và .
Lượt xem: 135,014 Cập nhật lúc: 21:11 07/05/2025
#8808 THPT Quốc giaToán
Cho mặt cầu có bán kính bằng 4, hình trụ có chiều cao bằng 4 và hai đường tròn đáy nằm trên . Gọi là thể tích khối trụ và là thể tích của khối cầu . Tỉ số bằng
Lượt xem: 149,900 Cập nhật lúc: 20:59 06/05/2025
#7697 THPT Quốc giaToán
Cho một cổ vật hình trụ có chiều cao đo được là , do bị hư hại nên khi tiến hành đo đạc lại thu được , với thuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây?
Lượt xem: 130,999 Cập nhật lúc: 22:57 07/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
954 xem60 thi
1 mã đề 50 câu hỏi 1 giờ 30 phút
4,393 xem324 thi
