Trong không gian
, cho điểm
A \left(\right. 2 \textrm{ } ; \textrm{ } 1 \textrm{ } ; \textrm{ } - 1 \right) và đường thẳng
. Viết phương trình mặt phẳng chứa
và cách
một khoảng lớn nhất
A.
.
B.
.
C.
.
D.
Đáp án đúng là: A
Trong không gian , cho điểm A \left(\right. 2 \textrm{ } ; \textrm{ } 1 \textrm{ } ; \textrm{ } - 1 \right) và đường thẳng . Viết phương trình mặt phẳng chứa và cách một khoảng lớn nhất
.
.
.
Đáp án đúng là: A
Trong không gian
, cho điểm
và đường thẳng
. Viết phương trình mặt phẳng chứa
và cách
một khoảng lớn nhất
A.
. B.
.
C.
. D.
Lời giải
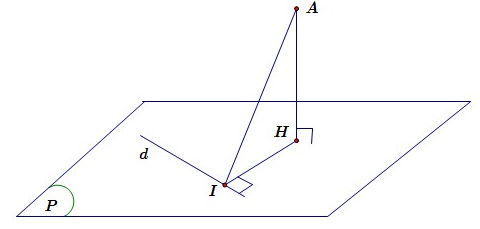
Gọi phương trình mặt phẳng chứa và cách một khoảng lớn nhất
Gọi lần lượt là hình chiếu của lên mặt phẳng và đường thẳng .
Ta có .
Mặt khác
Mặt khác
Dấu xảy ra khi
Phương trình mặt phẳng : .
Câu hỏi tương tự:
#8225 THPT Quốc giaToán
Trong không gian
, cho hai đường thẳng và đường thẳng . Đường thẳng đi qua điểm và cắt tại , cắt tại . Khi đó bằngLượt xem: 139,949 Cập nhật lúc: 18:54 25/04/2025
#8736 THPT Quốc giaToán
Trong không gian với hệ toạ độ , cho điểm và mặt phẳng . Đường thẳng đi qua điểm và vuông góc với mặt phẳng có phương trình tham số là:
Lượt xem: 148,728 Cập nhật lúc: 07:13 26/04/2025
#8781 THPT Quốc giaToán
Trong không gian
, cho hai điểm
và
. Đường thẳng
đi qua trung
điểm
của
và điểm
có phương trình là
Lượt xem: 149,425 Cập nhật lúc: 18:02 24/04/2025
#7780 THPT Quốc giaToán
Trong không gian , cho điểm , đường thẳng và mặt phẳng . Đường thẳng đi qua , cắt và song song với có phương trình là
Lượt xem: 132,410 Cập nhật lúc: 02:53 26/04/2025
#8194 THPT Quốc giaToán
Trong không gian , cho điểm , đường thẳng và mặt cầu . Biết điểm thuộc giao tuyến của mặt cầu và mặt phẳng . Khi điểm di động trên đường thẳng thì giá trị nhỏ nhất của biểu thức bằng
Lượt xem: 139,455 Cập nhật lúc: 16:33 25/04/2025
#8472 THPT Quốc giaToán
Trong không gian , cho điểm , mặt phẳng và mặt cầu . Gọi là đường thẳng đi qua , nằm trong và cắt tại hai điểm có khoảng cách nhỏ nhất. Phương trình của là
Lượt xem: 144,125 Cập nhật lúc: 19:32 25/04/2025
#7583 THPT Quốc giaToán
Trong không gian với hệ trục toạ độ , cho mặt cầu và điểm . Đường thẳng thay đổi, đi qua điểm và cắt mặt cầu tại hai điểm phân biệt. Tính diện tích lớn nhất của tam giác .
Lượt xem: 129,007 Cập nhật lúc: 07:12 26/04/2025
#7666 THPT Quốc giaToán
Trong không gian , cho hai đường thẳng ; . Gọi là đường thẳng đi qua , vuông góc với và cắt . Khi đó tọa độ giao điểm của và mặt phẳng là
Lượt xem: 130,402 Cập nhật lúc: 07:09 26/04/2025
#11181 THPT Quốc giaToán
Trong không gian , cho hai mặt cầu ; và điểm . Xét đường thẳng di động nhưng luôn tiếp xúc với đồng thời cắt tại hai điểm phân biệt. Diện tích lớn nhất của tam giác bằng
Lượt xem: 190,215 Cập nhật lúc: 22:10 25/04/2025
