Trong không gian
, cho điểm
, đường thẳng
và mặt cầu
. Biết điểm
thuộc giao tuyến của mặt cầu
và mặt phẳng
. Khi điểm
di động trên đường thẳng
thì giá trị nhỏ nhất của biểu thức
bằng
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: C
Trong không gian , cho điểm , đường thẳng và mặt cầu . Biết điểm thuộc giao tuyến của mặt cầu và mặt phẳng . Khi điểm di động trên đường thẳng thì giá trị nhỏ nhất của biểu thức bằng
.
.
.
.
Đáp án đúng là: C
Trong không gian
, cho điểm
, đường thẳng
và mặt cầu
. Biết điểm
thuộc giao tuyến của mặt cầu
và mặt phẳng
. Khi điểm
di động trên đường thẳng
thì giá trị nhỏ nhất của biểu thức
bằng
A.
. B.
. C.
. D.
.
Lời giải
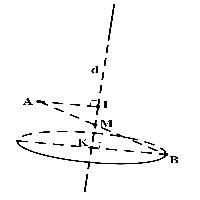
Mặt cầu có tâm và bán kính .
Đường thẳng có 1 véc-tơ chỉ phương là .
Gọi là giao điểm của mặt phẳng và đường thẳng . Vì nên là tâm của đường tròn giao tuyến và .
Ta có: và .
Ta tính được và .
Do di động trên đường thẳng (trục của đường tròn giao tuyến) và thuộc đường tròn giao tuyến nên biểu thức nhỏ nhất khi và chỉ khi .
Khi đó, ta có và . Suy ra , .
Ta có: .
Vậy .
Câu hỏi tương tự:
#8472 THPT Quốc giaToán
Trong không gian , cho điểm , mặt phẳng và mặt cầu . Gọi là đường thẳng đi qua , nằm trong và cắt tại hai điểm có khoảng cách nhỏ nhất. Phương trình của là
Lượt xem: 144,136 Cập nhật lúc: 17:00 17/05/2025
#8174 THPT Quốc giaToán
Trong không gian cho mặt phẳng đường thẳng và mặt cầu Gọi là hai điểm trên mặt cầu và là hai điểm nằm trên mặt phẳng sao cho cùng song song với đường thẳng Giá trị lớn nhất của tổng độ dài gần nhất với giá trị nào sau đây
Lượt xem: 139,124 Cập nhật lúc: 00:27 17/05/2025
#7583 THPT Quốc giaToán
Trong không gian với hệ trục toạ độ , cho mặt cầu và điểm . Đường thẳng thay đổi, đi qua điểm và cắt mặt cầu tại hai điểm phân biệt. Tính diện tích lớn nhất của tam giác .
Lượt xem: 129,020 Cập nhật lúc: 07:35 17/05/2025
#11181 THPT Quốc giaToán
Trong không gian , cho hai mặt cầu ; và điểm . Xét đường thẳng di động nhưng luôn tiếp xúc với đồng thời cắt tại hai điểm phân biệt. Diện tích lớn nhất của tam giác bằng
Lượt xem: 190,226 Cập nhật lúc: 19:55 14/05/2025
#7780 THPT Quốc giaToán
Trong không gian , cho điểm , đường thẳng và mặt phẳng . Đường thẳng đi qua , cắt và song song với có phương trình là
Lượt xem: 132,423 Cập nhật lúc: 16:59 17/05/2025
#7750 THPT Quốc giaToán
Trong không gian với hệ trục tọa độ , cho đường thẳng và mặt phẳng lần lượt có phương trình và , điểm . Đường thẳng cắt và lần lượt tại và sao cho là trung điểm của đoạn thẳng đi qua điểm . Tổng bằng
Lượt xem: 131,841 Cập nhật lúc: 10:40 17/05/2025
#7763 THPT Quốc giaToán
Trong không gian với hệ tọa độ , cho đường thẳng và mặt phẳng . Phương trình đường thẳng nằm trong , cắt và tạo với một góc đi qua điểm nào sau đây:
Lượt xem: 132,159 Cập nhật lúc: 06:51 16/05/2025
#8736 THPT Quốc giaToán
Trong không gian với hệ toạ độ , cho điểm và mặt phẳng . Đường thẳng đi qua điểm và vuông góc với mặt phẳng có phương trình tham số là:
Lượt xem: 148,738 Cập nhật lúc: 13:46 17/05/2025
#11177 THPT Quốc giaToán
Trong không gian , cho điểm và đường thẳng . Viết phương trình mặt phẳng chứa và cách một khoảng lớn nhất
Lượt xem: 190,115 Cập nhật lúc: 06:23 15/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
1,370 xem96 thi
