
20 Đề thi thử THPTQG môn Toán mới nhất cực hay có lời giải
Tài liệu gồm 20 đề thi thử THPT Quốc gia môn Toán mới nhất, với nội dung bám sát chương trình học. Đề thi bao gồm các câu hỏi đa dạng về giải tích, logarit, và bài toán thực tế, kèm đáp án chi tiết.
Từ khoá: Toán học giải tích logarit bài toán thực tế ôn thi tốt nghiệp năm 2022 đề thi có đáp án
Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết📘 Tuyển Tập Đề Thi Tham Khảo Các Môn THPT Quốc Gia 2025 🎯
Số câu hỏi: 947 câuSố mã đề: 20 đềThời gian: 1 giờ
175,239 lượt xem 13,473 lượt làm bài
Xem trước nội dung:
Trong các biểu thức sau, biểu thức nào có nghĩa?
Mệnh đề nào dưới đây sai?
Hàm số tuần hoàn với chu kì π
Hàm số tuần hoàn với chu kì π
Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường thẳng đó
Biết rằng nghịch đảo của số phức bằng số phức liên hợp của nó. Mệnh đề nào dưới đây đúng?
Mệnh đề nào dưới đây đúng?
Ba số hạng đầu tiên của một cấp số nhân lần lượt là . Tìm số hạng thứ tư của cấp số nhân đó
Biết phương trình có hai nghiệm trên tập số phức. Tính giá trị biểu thức
Trong không gian Oxyz cho hình hộp ABCD A'B'C'D'. Biết , và . Tìm tọa độ đỉnh D'.
Cho hàm số . Gọi M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Tìm .
Tìm số nghiệm của phương trình .
Trên hai đường thẳng song song và lấy 6 điểm phân biệt, 4 điểm thuộc và 2 điểm thuộc . Tính số tam giác được tạo thành từ 6 điểm đã cho.
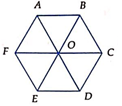
Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay . Tìm α.
Tìm tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số .
Hàm số nào dưới đây có tính chất: Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình là một đường thẳng song song với trục hoành.
Cho hình tứ diện ABCD có AD vuông góc với mặt phẳng (ABC), tam giác ABC có , . Tính góc giữa hai mặt phẳng (ABC) và (DBC), biết khối tứ diện ABCD có thể tích bằng .
Cho a là một số thực dương và b là một số nguyên, . Hỏi có bao nhiêu cặp số thỏa mãn điều kiện ?
Tính diện tích hình phẳng giới hạn bởi đường cong , tiếp tuyến với đường cong đó tại điểm có hoành độ bằng 2 và trục Oy.
Cho tứ diện đều S.ABC. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng song song với . Tính chu vi của thiết diện tạo bởi và tứ diện S.ABC tính theo .
Một hộp chứa hai viên bi đỏ, 2 viên bi xanh và 2 viên bi vàng. Bạn Hà lấy ngẫu nhiên từ hộp ra 2 viên bi. Sau đó bạn Lâm lấy ngẫu nhiên từ hộp ra 2 viên bi nữa. 2 viên bi còn lại trong hộp được bạn Anh lấy ra nốt. Tính xác suất để 2 viên bi bạn Anh lấy ra có cùng màu.
Cho hàm số . Tính giá trị biểu thức
Trong không gian Oxyz cho đường thẳng Δ có phương trình . Tìm phương trình tham số của đường thẳng d là hình chiếu vuông góc của Δ trên mặt phẳng .
Gọi (cm) là mức nước ở một bồn chứa sau khi bơm nước vào bồn được t giây. Biết rằng và lúc đầu bồn không có nước. Tìm mức nước ở bồn sau khi bơm nước được 56 giây.
Cho các hàm số và . Tính giới hạn .
Cho hình hộp chữ nhật ABCD A'B'C'D' có . Tính bán kính đường tròn là giao tuyến của mặt phẳng với mặt cầu đi qua 8 đỉnh của hình hộp.
Một máy tính cầm tay bị hỏng không hiển thị được chữ số 1. Chẳng hạn nếu ta bấm số 3131 thì chỉ có số 33 được hiển thị trên màn hình (hai chữ số 3 viết liền nhau, không có khoảng trắng ở giữa). Bạn Hà đã bấm một số có 6 chữ số nhưng chỉ có số 2007 xuất hiện trên màn hình. Tìm số các số mà bạn Hà có thể đã nhập vào máy tính.
Trong không gian Oxyz, viết phương trình mặt phẳng chứa hai đường thẳng và .
Tính khoảng cách từ điểm đến đường thẳng .
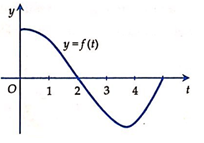
Xét hàm số trong đó hàm số có đồ thị như hình vẽ bên. Giá trị nào dưới đây là lớn nhất?
Biết các số phức được biểu diễn bởi ba đỉnh của một hình bình hành nào đó trong mặt phẳng phức. Trong các số phức sau, tìm số phức được biểu diễn bởi đỉnh còn lại.
Trong không gian Oxyz cho ba điểm , và . Tìm tọa độ điểm I trên mặt phẳng (Oxy) sao cho biểu thức đạt giá trị nhỏ nhất.
Cho hàm số có bảng biến thiên dưới đây
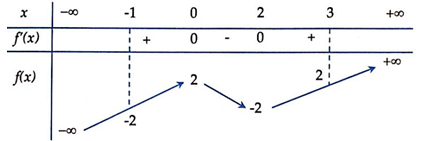
Tìm tất cả các giá trị thực của tham số m để phương trình có ba nghiệm thực phân biệt.
Cho hình phẳng D giới hạn bởi đồ thị các hàm số và . Biết thể tích khối tròn xoay dc tạo thành khi quay D quanh trục Ox bằng , trong đó a và b là các số tự nhiên nguyên tố cùng nhau. Tìm .
Cho hình lập phương ABCD A'B'C'D' có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BD' và B'C.
Cho hàm số có đồ thị là (H) và đường thẳng d có hệ số góc m và đi qua điểm . Giả sử d cắt (H) tại hai điểm phân biệt M, N. Qua M kẻ các đường thẳng lần lượt song song với các trục tọa độ, qua N kẻ các đường thẳng lần lượt song song với các trục tọa độ. Tìm số các giá trị thực của tham số m sao cho bốn đường thẳng đó tạo thành một hình vuông.
Cho là một hàm liên tục trên R. Biết , tính .
Cho khối chóp cụt ABC A'B'C' với hai đáy ABC và A'B'C' có diện tích lần lượt bằng 4 và 9. Mặt phẳng (ABC') chia khối chóp cụt thành hai phần. Gọi là phần chứa đỉnh C và là phần còn lại. Tính tỉ số thể tích và .
Có bao nhiêu điểm trên trục tung sao cho từ đó kẻ được ba tiếp tuyến khác nhau đến đồ thị hàm số ?
Một cấp số nhân lùi vô hạn có tổng bằng S. Biết số hạng thứ hai của cấp số nhân đó bằng 1. Tìm giá trị nhỏ nhất có thể của S
Cho hàm số . Tìm tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn .
Một hình hộp chữ nhật có kích thước a (cm) × b (cm) × c (cm), trong đó a, b, c là các số nguyên và . Gọi S (cm3) và S (cm2) lần lượt là thể tích và diện tích toàn phần của hình hộp. Biết , tìm số các bộ ba số ?
Cho phương trình . Gọi T là tập hợp tất cả các giá trị thực của tham số m sao cho phương trình có nghiệm dương. Mệnh đề nào dưới đây đúng?
Biết , trong đó a và b là các số tự nhiên nguyên tố cùng nhau. Tìm .
Một hình trụ có bán kính bằng r và chiều cao . Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa hai đường thẳng AB và trục của hình trụ bằng 30°. Tính khoảng cách giữa đường thẳng AB và trục của hình trụ.
Cho f(x) là một hàm liên tục trên R và a là một số thực lớn hơn 1. Mệnh đề nào dưới đây sai?
Trong mặt phẳng tọa độ xét ba điểm A, B, C theo thứ tự biểu diễn ba số phức thỏa mãn và . Hỏi tam giác ABC là tam giác gì?
Cho hình tứ diện đều (H). Gọi (H') là hình tứ diện đều có các đỉnh là tâm các mặt của (H). Tính tỉ số diện tích toàn phần của (H') và (H).
Cho phương trình . Tính tổng tất cả các nghiệm thực dương của phương trình.
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (C). Gọi h là chiều cao của hình nón. Tìm h để thể tích của khối nón là lớn nhất.
Cho biểu thức . Biểu thức A có giá trị thuộc khoảng nào trong các khoảng dưới đây?
Cho một chiếc cốc có dạng hình nón cụt và một viên bi có đường kính bằng chiều cao của cốc. Đổ đầy nước vào cốc rồi thả viên bi vào, ta thấy lượng nước tràn ra bằng một nửa lượng nước đổ vào cốc lúc ban đầu. Biết viên bi tiếp xúc với đáy cốc và thành cốc. Tìm tỉ số bán kính của miệng cốc và đáy cốc (bỏ qua độ dày của cốc).
Đề thi tương tự
20 mã đề 1001 câu hỏi 1 giờ
167,229 xem12,857 thi
20 mã đề 1000 câu hỏi 1 giờ
159,588 xem12,270 thi
20 mã đề 989 câu hỏi 1 giờ
184,058 xem14,151 thi
20 mã đề 903 câu hỏi 1 giờ
154,996 xem11,906 thi
1 mã đề 50 câu hỏi 1 giờ
93,199 xem7,161 thi
1 mã đề 50 câu hỏi 50 phút
505 xem20 thi
1 mã đề 50 câu hỏi 1 giờ 30 phút
5,100 xem378 thi
