Ôn thi Tốt nghiệp THPT môn Toán (Đề 18)

Trên khoảng từ $\left(1;+\infty \right)$, đạo hàm của hàm số $y=\ln \left(x-1\right)$  là

Với a, b là các số thực dương bất kỳ, ${\log }_2\frac{a}{b^2}$  bằng

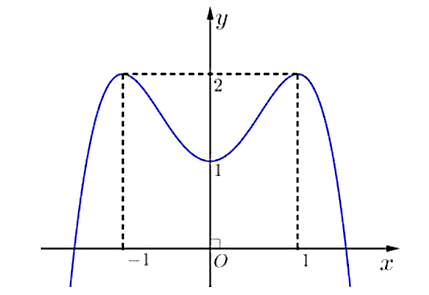
Cho hàm số y = f(x) có đồ thị là đường cong hình bên dưới. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Cho hàm số f(x) liên tục trên $ℝ$ và có $\underset{0}{\overset{2}{\int }}f\left(x\right)\text{d}x=9;\underset{2}{\overset{4}{\int }}f\left(x\right)\text{d}x=4$ . Khi đó $\underset{0}{\overset{4}{\int }}f\left(x\right)\text{d}x$  bằng

Biết tập nghiệm của bất phương trình $3^x<4-3^{1-x}$  là (a; b). Giá trị a + b bằng

Cho hàm số $\int \left(1+\sin x\right)\text{\hspace{0.17em}d}x=F\left(x\right)+C$ . Khẳng định nào dưới đây đúng?

Cho hàm số $f\left(x\right)=e^{1-2023x}$ . Trong các khẳng định sau, khẳng định nào đúng?

Cho hình nón có đường kính đáy bằng 6, độ dài đường sinh bằng 5. Diện tích xung quanh hình nón đã cho bằng

Phần thực của số phức z = -4 - i là

Cho hàm số y = f(x) có đồ thị là đường cong như hình vẽ bên. Giá trị cực tiểu của hàm số đã cho là.

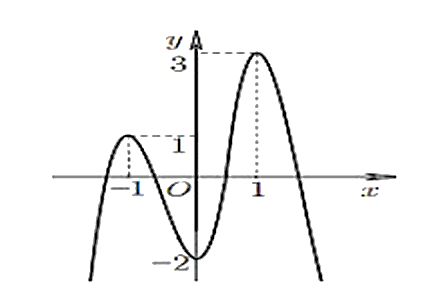
Cho hàm số  $y=a{x}^4+b{x}^2+c\left(a\ne 0\right)$ có đồ thị như hình vẽ:

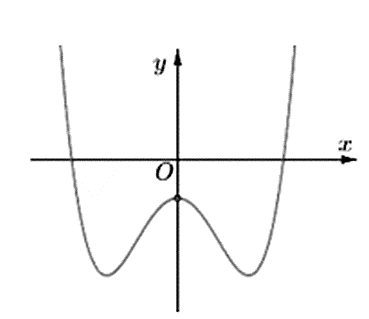
Mệnh đề nào đúng?

Một đội văn nghệ có 5 bạn nam và 3 bạn nữ. Có bao nhiêu cách chọn 2 bạn gồm 1 bạn nam và 1 bạn nữ để thể hiện một tiết mục hát song ca?

Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn các số phức z thỏa mãn $\left|z+2-3i\right|=4$ là một đường tròn. Tâm của đường tròn đó có tọa độ là

Trong không gian Oxyz, cho mặt cầu $\left(S\right):x^2+y^2+z^2-4x+2y-1=0$ . Điểm nào sau đây thuộc mặt cầu (S)?

Trong không gian Oxyz, góc giữa trục Oy và mặt phẳng (Oxz) bằng

Cho hàm số y = f(x) có bảng biến thiên như sau:

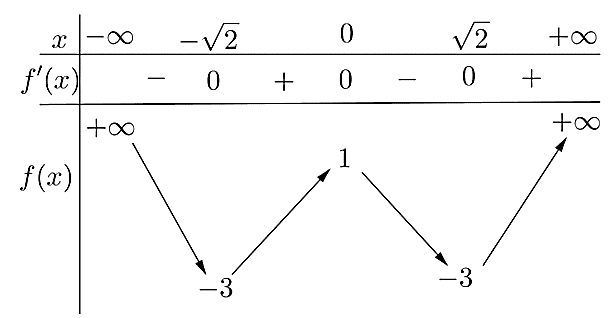
Hàm số đã cho đạt cực đại tại

Tập nghiệm của bất phương trình ${\log }_{\frac{1}{2}}\left(x-2\right)\le 1$  là

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a, cạnh bên SA vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA và CD bằng

Khối lập phương có độ dài đường chéo là $3\sqrt{3}$ . Thể tích của khối lập phương đã cho là

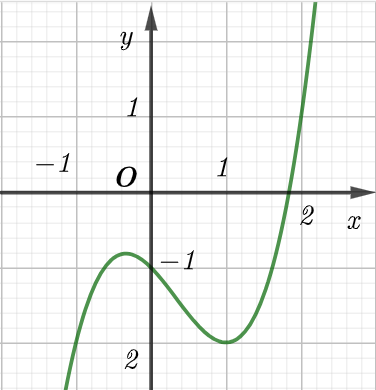
Cho hàm số $y=a{x}^3+b{x}^2+cx+d$  có đồ thị là đường cong trong hình bên. Tọa độ giao điểm của đồ thị hàm số đã cho và đường thẳng y = 1 là

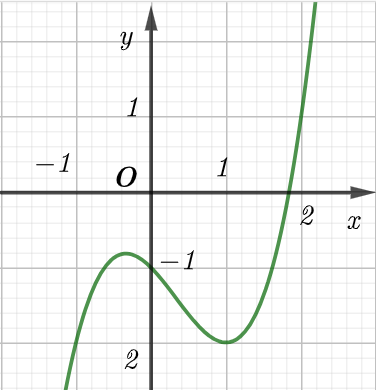
Cho hàm số $y=a{x}^3+b{x}^2+cx+d$  có đồ thị là đường cong trong hình bên. Tọa độ giao điểm của đồ thị hàm số đã cho và đường thẳng y = 1 là

Tập nghiệm của bất phương trình ${\left(\frac{1}{3}\right)}^{x+1}>3$  là

Nếu $\underset{-1}{\overset{2}{\int }}f\left(x\right)\text{d}x=2$  thì $I=\underset{-1}{\overset{2}{\int }}\left[x+2f\left(x\right)\right]\text{d}x$  bằng

Trong không gian Oxyz, đường thẳng $d:\frac{x+3}{4}=\frac{y-2}{3}=\frac{z-1}{2}$  có một vectơ chỉ phương có tọa độ là

Thể tích khối tròn xoay thu được khi quay hình phẳng giới hạn bởi hai đường $y=x^2-4x+3$  và y = 0 quanh trục Ox bằng

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy và $SA=\frac{a\sqrt{6}}{2}$  (tham khảo hình vẽ). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng

Trong không gian Oxyz, cho mặt phẳng $\left(P\right):\frac{x}{2}+\frac{y}{3}-\frac{z}{2}=1$ . Một vectơ pháp tuyến của mặt phẳng (P) là

Một nhóm gồm 2 người đàn ông, 3 người phụ nữ và 4 trẻ em. Chọn ngẫu nhiên 4 người từ nhóm đó. Xác suất để 4 người được chọn: có cả đàn ông, phụ nữ và trẻ em bằng

Số phức liên hợp của $z={\left(1+i\right)}^2$  là

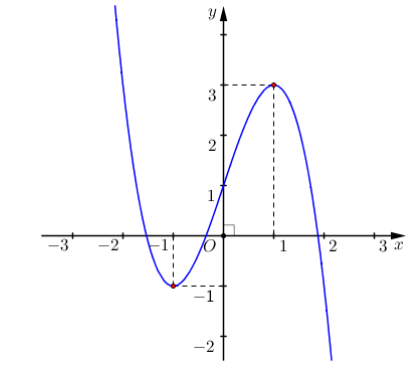
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên dương của m để phương trình f(x) = m có ba nghiệm phân biệt?

Trong không gian Oxyz, cho hai điểm M(4;-2;1) và N(5;2;3). Đường thẳng MN có phương trình là

Trong không gian Oxyz, cho A(1;2;3). Điểm đối xứng với A qua trục Oz có tọa độ là

Phương trình đường tiệm cận ngang của đồ thị $y=\frac{-2x-1}{x-2}$ ?

Một mặt phẳng $\left(\alpha \right)$  cắt mặt cầu theo một thiết diện là đường tròn có bán kính $r<R$ . Gọi d là khoảng cách từ I đến $\left(\alpha \right)$ . Khẳng định nào sau đây là đúng?

Trong không gian tọa độ Oxyz cho điểm A(-3;1-3) và đường thẳng $d:\frac{x+1}{2}=\frac{y-2}{-3}=\frac{z}{1}$ . Gọi $\left(\alpha \right)$  là mặt phẳng chứa đường thẳng d và vuông góc với mặt phẳng tọa độ (Oyz). Khoảng cách từ A đến mặt phẳng $\left(\alpha \right)$  bằng

Biết tập nghiệm của bất phương trình ${{\log }_2}^2\left(x^2-1\right)-{\log }_3\left(x^2-1\right)+{\log }_2\frac{2}{3}{\log }_{3}2\le 0$ là $S=\left[a;b\right]\cup \left[c;d\right]$  với $a<b<c<d$ . Giá trị của biểu thức a + b +c + 2d bằng

Có bao nhiêu cặp số nguyên (x;y) thỏa mãn

${\log }_3\left(x^2+4y^2+x\right)+{\log }_2\left(x^2+4y^2\right)+\frac{x^2-8x+4y^2}{x}\le {\log }_{3}x+{\log }_2\left(x^2+4y^2+24x\right)$?

Có bao nhiêu giá trị nguyên của tham số m để hàm số $y=x^4-4x^3+\left(4-m\right)x+1$  có ba điểm cực trị?

Trên tập hợp số phức, xét phương trình $z^2-2\left(m+1\right)z+m^2+2=0$  (m tham số). Có tất cả bao nhiêu giá trị của tham số m để phương trình có hai nghiệm phân biệt $z_1;z_2$ thỏa mãn $\left|z_1\right|+\left|z_2\right|=8$ ?

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left(P\right):x+y-z+2=0$ và hai điểm A(3;4;1), B(7;-4;-3). Điểm M(a;b;c) trên (P) sao cho tam giác ABM vuông tại M và có diện tích nhỏ nhất. Khi a > 2  thì biểu thức T = a + b - c có giá trị bằng

Biết F(x) và G(x) là hai nguyên hàm của hàm số f(x) trên $ℝ$  và thoả mãn $\underset{0}{\overset{4}{\int }}f\left(x\right)\text{d}x=F\left(4\right)-G\left(0\right)+2m$ , với m > 0. Gọi S là diện tích hình phẳng giới hạn bởi các đường $y=F\left(x\right)$ , $y=G\left(x\right)$ ; $x=0$  và $x=4$ . Khi S = 8 thì m bằng

Trong các số phức z thoả mãn điều kiện $\left|z-2-5i\right|=\left|z-3i\right|$ , biết rằng $z=x+yi,$ $\left(x,y\in ℝ\right)$  có môđun nhỏ nhất. Tính  $P=x^2+y^2.$

Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với mặt phẳng đáy. Biết góc giữa SC và mặt phẳng đáy bằng $60°$  và khoảng cách từ A đến mặt phẳng (SBC) bằng $a\sqrt{6}$ . Thể tích khối chóp S.ABCD bằng

Cho hàm số $f\left(x\right)=\left|-\frac{1}{3}{x}^3+\frac{1}{2}\left(2m+3\right)x^2-\left(m^2+3m\right)x+\frac{2}{3}\right|$ . Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-20;23] để hàm số nghịch biến trên khoảng (1;2)?

Cho hàm số y = f(x) liên tục trên $ℝ$ , thỏa mãn $f^{\text{'}}\left(x\right)-f\left(x\right)=-8+16x-4x^2$  và $f\left(0\right)=0$ . Thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và trục Ox quay quanh Ox bằng