Trắc nghiệm Toán 10 Bài hệ thức lượng trong tam giác có đáp án (Mới nhất)

Tam giác ABC có $AB=\mathrm{5,}BC=\mathrm{7,}CA=8$. Số đo góc $\widehat{A}$bằng:

Tam giác ABC có $AB=\mathrm{2,}AC=1$và $\widehat{A}=60°$. Tính độ dài cạnh BC.

Tam giác ABC có $AB=\sqrt{2},AC=\sqrt{3}$và $\widehat{C}=45°$. Tính độ dài cạnh BC.

Tam giác ABC có $\widehat{B}=60°,\widehat{C}=45°$và AB = 5. Tính độ dài cạnh AC.

Cho hình thoi ABCD cạnh bằng 1cm và có $\widehat{BAD}=60°$. Tính độ dài cạnh AC.

Tam giác ABC có $AB=\mathrm{4,}BC=\mathrm{6,}AC=2\sqrt{7}$. Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM.

Tam giác ABC có $AB=\frac{\sqrt{6}-\sqrt{2}}{2},BC=\sqrt{3},CA=\sqrt{2}$. Gọi D là chân đường phân giác trong góc $\widehat{A}$. Khi đó góc $\widehat{ADB}$bằng bao nhiêu độ?

Tam giác ABC vuông tại A, đường cao $AH=32cm$. Hai cạnh AB và AC tỉ lệ với 3 và 4. Cạnh nhỏ nhất của tam giác này có độ dài bằng bao nhiêu?

Tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc $\widehat{MPE},\widehat{EPF},\widehat{FPQ}$bằng nhau. Đặt $MP=q,PQ=m,PE=x,PF=y$. Trong các hệ thức sau, hệ thức nào đúng?

Cho góc $\widehat{xOy}=30°$. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:

Cho góc $\widehat{xOy}=30°$. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng:

Tam giác ABC có $AB=c,BC=a,CA=b$. Các cạnh a, b, c liên hệ với nhau bởi đẳng thức $b\left(b^2-a^2\right)=c\left(a^2-c^2\right)$. Khi đó góc $\widehat{BAC}$bằng bao nhiêu độ?

Tam giác ABC vuông tại A, có $AB=c,AC=b$. Gọi ${\mathcal{l}}_a$là độ dài đoạn phân giác trong góc $\widehat{BAC}$. Tính ${\mathcal{l}}_a$theo a và b.

Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau góc $60°$. Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?

Kết quả gần nhất với số nào sau đây?

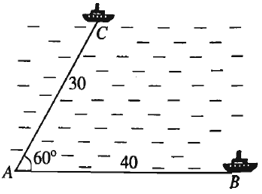
Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách AB = 40 m, $\widehat{CAB}={45}^0$và $\widehat{CBA}={70}^0$.

Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây?

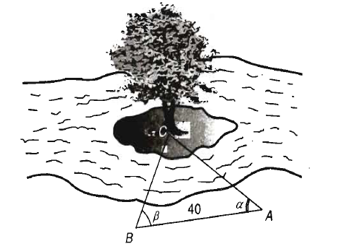
Từ vị trí A người ta quan sát một cây cao (hình vẽ).

Biết $AH=4\text{m},HB=20\text{m},\widehat{BAC}={45}^0$.

Chiều cao của cây gần nhất với giá trị nào sau đây?

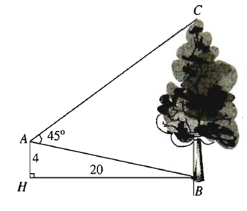
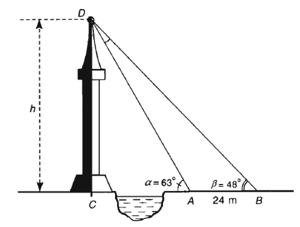
Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B và C thẳng hàng. Ta đo được AB = 24 m, $\widehat{CAD}={63}^0,\widehat{CBD}={48}^0$.

Chiều cao h của tháp gần với giá trị nào sau đây?

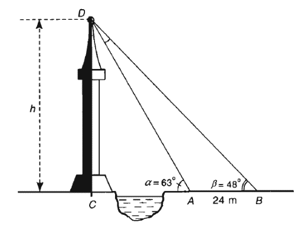
Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B và C thẳng hàng. Ta đo được AB = 24 m, $\widehat{CAD}={63}^0,\widehat{CBD}={48}^0$.

Chiều cao h của tháp gần với giá trị nào sau đây?

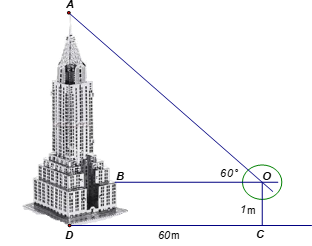
Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng CD = 6cm, giả sử chiều cao của giác kế là OC = 1m.

Quay thanh giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh A của tháp. Đọc trên giác kế số đo của góc $\widehat{AOB}={60}^0$. Chiều cao của ngọn tháp gần với giá trị nào sau đây:

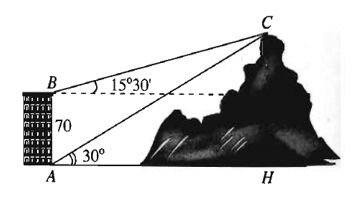
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AAC tạo với phương nằm ngang góc 30 $°$, phương nhìn BC tạo với phương nằm ngang góc ${15}^{0}30\text{'}$.

Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?

Tam giác ABC có $AB=6\text{cm},AC=8\text{cm}$và BC = 10 cm. Độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác bằng:

Tam giác ABC có AB = 9 cm, AC = 12 cm và BC = 12 cm. Tính độ dài đường trung tuyến AM của tam giác đã cho.

Tam giác ABCcân tại C, có AB = 9cm và $AC=\frac{15}{2}\text{cm}$. Gọi D là điểm đối xứng của B qua C. Tính độ dài cạnh AD

Tam giác ABC có $AB=\mathrm{3,}BC=8$. Gọi M là trung điểm của BC. Biết $\cos \widehat{AMB}=\frac{5\sqrt{13}}{26}$và $AM>3$. Tính độ dài cạnh AC.

Tam giác ABC có trọng tâm G. Hai trung tuyến $BM=6$, $CN=9$và $\widehat{BGC}={120}^0$. Tính độ dài cạnh AB.

Tam giác ABC có độ dài ba trung tuyến lần lượt là 9, 12, 15. Diện tích của tam giác ABC bằng:

Cho tam giác ABC có $AB=c,BC=a,CA=b$. Nếu giữa a, b, c có liên hệ $b^2+c^2=2a^2$thì độ dài đường trung tuyến xuất phát từ đỉnh A của tam giác tính theo a bằng:

Tam giác ABC có $AB=c,BC=a,CA=b$. Các cạnh a, b, c liên hệ với nhau bởi đẳng thức $a^2+b^2=5c^2$. Góc giữa hai trung tuyến AM và BN là góc nào?

Tam giác ABC có $AB=c,BC=a,CA=b$. Gọi $m_a,m_b,m_c$là độ dài ba đường trung tuyến, G trọng tâm. Xét các khẳng định sau:

Tam giác ABC có BC = 10 và $\widehat{A}={30}^{\text{O}}$. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC

Tam giác ABC có $AB=\mathrm{3,}AC=6$và $\widehat{A}=60°$. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

Tam giác ABC có $BC=21\text{cm},CA=17\text{cm},AB=10\text{cm}$. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R. Khi đó bán kính R bằng:

Tam giác ABC vuông tại A có đường cao $AH=\frac{12}{5}\text{cm}$và $\frac{AB}{AC}=\frac{3}{4}$. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.

Cho tam giác ABC có $AB=3\sqrt{3},BC=6\sqrt{3}$và CA = 9. Gọi D là trung điểm BC. Tính bán kính R của đường tròn ngoại tiếp tam giác ABD

Tam giác nhọn ABC có $AC=b,BC=a$, BB' là đường cao kẻ từ B và $\widehat{CBB\text{'}}=\alpha$. Bán kính đường tròn ngoại tiếp R của tam giác ABC được tính theo a, b và $\alpha$là:

Tam giác ABC có $AB=\mathrm{3,}AC=\mathrm{6,}\widehat{BAC}=60°$. Tính diện tích tam giác ABC.

Tam giác ABC có $AC=\mathrm{4,}\widehat{BAC}=30°,\widehat{ACB}=75°$. Tính diện tích tam giác ABC.

Tam giác ABC có $a=\mathrm{21,}b=\mathrm{17,}c=10$. Diện tích của tam giác ABC bằng:

Tam giác ABC có $AB=\mathrm{3,}AC=\mathrm{6,}\widehat{BAC}=60°$. Tính độ dài đường cao $h_a$của tam giác.

Tam giác ABC có $AC=\mathrm{4,}\widehat{ACB}=60°$. Tính độ dài đường cao h uất phát từ đỉnh A của tam giác.

Tam giác ABC có $a=\mathrm{21,}b=\mathrm{17,}c=10$. Gọi B' là hình chiếu vuông góc của B trên cạnh AC. Tính BB'.

Tam giác ABC có AB = 8 cm, AC = 18 cm và có diện tích bằng 64 ${\text{cm}}^{\text{2}}$. Giá trị sin A bằng:

Hình bình hành ABCD có $AB=a,BC=a\sqrt{2}$và $\widehat{BAD}={45}^0$. Khi đó hình bình hành có diện tích bằng:

Tam giác ABC vuông tại A có $AB=AC=30$cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:

Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:

Tam giác ABC có $BC=2\sqrt{3},AC=2AB$và độ dài đường cao AH = 2. Tính độ dài cạnh AB.

Tam giác ABC có $BC=a,CA=b,AB=c$và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:

Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc B bằng:

Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có BC = 3, góc $\widehat{BAC}={30}^0$. Tính diện tích tam giác ABC.

Tam giác ABC có $AB=\mathrm{5,}AC=8$và $\widehat{BAC}={60}^0$. Tính bán kính r của đường tròn nội tiếp tam giác đã cho.

Tam giác ABC có $a=\mathrm{21,}b=\mathrm{17,}c=10$. Tính bán kính r của đường tròn nội tiếp tam giác đã cho.

Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a.

Tam giác ABC vuông tại A có AB = 6 cm, BC = 10 cm. Tính bán kính r của đường tròn nội tiếp tam giác đã cho.

Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi rr là bán kính đường tròn nội tiếp tam giác ABC. Khi đó tỉ số $\frac{R}{r}$bằng: