Có bao nhiêu số thực $c$ để hình phẳng giới hạn bởi đồ thị hàm số $y = x^{2} - 4 x + c$, trục hoành và các đường thẳng $x = 2$; $x = 4$ có diện tích bằng 3?

A.  

0.

B.  

1.

C.  

2.

D.  

3.

Đáp án đúng là: C

Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x^{2} - 4 x + c$, trục hoành và các đường thẳng $x = 2$; $x = 4$ là $S = \int_{2}^{4} \left| x^{2} - 4 x + c \left|\right. \text{d} x$.
Với $c \geq 4$:

$S = \int_{2}^{4} \left(\right. x^{2} - 4 x + c \right) \text{d} x = \left( \left( \dfrac{1}{3} x^{3} - 2 x^{2} + c x \right) \left|\right)_{2}^{4} = - \dfrac{16}{3} + 2 c$
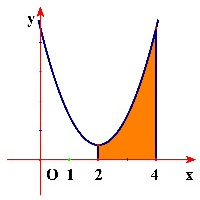
$S = 3 \Rightarrow \dfrac{- 16}{3} + 2 c = 3 \Leftrightarrow c = \dfrac{25}{6}$ (thỏa mãn)
Với $0 < c < 4$:

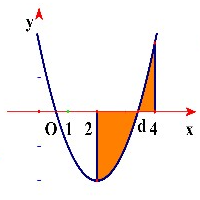
$d$ là hoành độ giao điểm của đồ thị hàm số $y = x^{2} - 4 x + c$ và trục hoành, $d > 2$ nên $d^{2} - 4 d + c = 0 \Leftrightarrow d = 2 + \sqrt{4 - c}$.
$S = \int_{2}^{d} \left(\right. - x^{2} + 4 x - c \right) \text{d} x + \int_{d}^{4} \left( x^{2} - 4 x + c \right) \text{d} x$
$= \left( \left( \dfrac{- 1}{3} x^{3} + 2 x^{2} - c x \right) \left|\right.\right)_{2}^{d} + \left( \left( \dfrac{1}{3} x^{3} - 2 x^{2} + c x \right) \left|\right)_{d}^{4}$
$= \dfrac{- 2}{3} d^{3} + 4 d^{2} - 2 c d - 16 + 6 c$
$= \dfrac{- 2}{3} \left(\right. 2 + \sqrt{4 - c} \right)^{3} + 4 \left( 2 + \sqrt{4 - c} \right)^{2} - 2 c \cdot \left( 2 + \sqrt{4 - c} \right) - 16 + 6 c$
Đặt $t = \sqrt{4 - c}$, khi đó $0 < t < 2$ và $S = - \dfrac{2}{3} \left( - 2 t^{3} + 3 t^{2} - 4 \right)$
$S = 3$ suy ra $\dfrac{- 2}{3} \left( - 2 t^{3} + 3 t^{2} - 4 \right) = 3 \Leftrightarrow - 2 t^{3} + 3 t^{2} + \dfrac{1}{2} = 0$.
Sử dụng máy tính, giải phương trình trên suy ra $t \approx 1 , 5979$ nên $c \approx 1 , 4467$ (thỏa mãn).
Với $c \leq 0$:

$S = \int_{2}^{4} \left( - x^{2} + 4 x - c \right) \text{d} x = \left( \left( \dfrac{- 1}{3} x^{3} + 2 x^{2} - c x \right) \left|\right.\right)_{2}^{4} = \dfrac{16}{3} - 2 c$
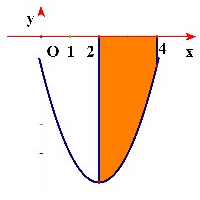
$S = 3$ suy ra $\dfrac{16}{3} - 2 c = 3 \Leftrightarrow c = \dfrac{7}{6}$ (không thỏa mãn $c \leq 0$).
Vậy có 2 giá trị của $c$ thỏa mãn ycbt.