Cho bất phương trình
. Có bao nhiêu số nguyên dương
để bất phương trình nghiệm đúng với
.
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: C
Cho bất phương trình . Có bao nhiêu số nguyên dương để bất phương trình nghiệm đúng với .
.
.
.
.
Đáp án đúng là: C
Cho hàm số
liên tục trên
và có đồ thị như hình vẽ dưới đây.
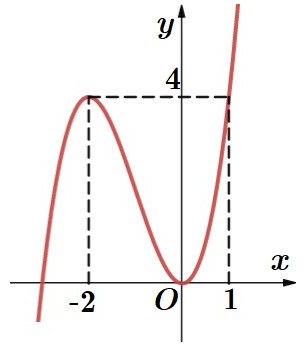
Tập hợp tất cả các giá trị thực của tham số để phương trình có nghiệm thuộc khoảng là
A. B. C. D.
Lời giải
Đặt .
Để có nghiệm thuộc khoảng .
Câu hỏi tương tự:
#8785 THPT Quốc giaToán
Có bao nhiêu số nguyên dương sao cho có ứng với giá trị của , bất phương trình có đúng 9 nghiệm nguyên?
Lượt xem: 149,399 Cập nhật lúc: 14:53 26/04/2025
#7856 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có bảng biến thiên như hình sau:
Có bao nhiêu giá trị nguyên dương của tham số để bất phương trình nghiệm đúng với mọi
Lượt xem: 133,720 Cập nhật lúc: 18:53 26/04/2025
#6975 THPT Quốc giaVật lý
Một người có khối lượng treo mình vào sợi dây bungee đàn hồi có hệ số đàn hồi . Từ vị trí cân bằng người này được kéo thêm so với vị trí cân bằng và thả cho hệ dao động điều hòa. Chọn trục tọa độ theo phương thẳng đứng, gốc tại vị trí cân bằng của hệ, chiều dương hướng xuống, gốc thời gian là lúc hệ bắt đầu dao động. Phương trình li độ của hệ được viết như sau:
Lượt xem: 118,762 Cập nhật lúc: 14:24 26/04/2025
#944 THPT Quốc giaVật lý
Một người khối lượng treo mình vào sợi dây đàn hồi có hệ số đàn hồi (Hình vẽ). Từ vị trí cân bằng người này được kéo lên so với vị trí cân bằng và thả cho hệ dao động điều hoà. Chọn trục tọa độ theo phương thẳng đứng, gốc tại vị trí cân bằng của hệ, chiều dương hướng xuống, gốc thời gian là lúc hệ bắt đầu dao động. Phương trình li độ của hệ là
Lượt xem: 16,114 Cập nhật lúc: 22:03 26/04/2025
#2046 THPT Quốc giaVật lý
Cho hai vật m1 và m2 có khối lượng lần lượt là 100 g và 150 g gắn vào hai đầu một lò xo có độ cứng 100 N/m. Hệ được đặt trên một mặt sàn nằm ngang như hình vẽ. Đưa m1 đến vị trí lò xo nén 3 cm rồi truyền cho nó một vận tốc cm/s hướng thẳng đứng từ trên xuống. Bỏ qua mọi ma sát. Biết trong quá trình dao động, trục của lò xo luôn có phương thẳng đứng. Lấy g =10 m/s2, π2 = 10. Tốc độ trung bình của m1 kể từ thời điểm truyền vận tốc cho m1 đến thời điểm m2 bắt đầu rời khỏi mặt sàn là
Lượt xem: 34,904 Cập nhật lúc: 18:43 26/04/2025
#1979 THPT Quốc giaVật lý
Một vật trượt không vận tốc ban đầu từ đỉnh mặt phẳng nghiêng, nghiêng góc so với phương ngang. Hệ số ma sát giữa vật và mặt phẳng nghiêng phụ thuộc vào khoảng cách x tính từ vị trí của vật đang trượt tới đỉnh mặt phẳng nghiêng theo quy luật , trong đó x tính bằng mét. Biết mặt phẳng nghiêng đủ dài để vật dừng lại phía trên chân mặt phẳng nghiêng. Lấy . Khoảng thời gian kể từ lúc vật bắt đầu trượt cho tới khi vật dừng lại gần giá trị nào nhất sau đây:
Lượt xem: 33,865 Cập nhật lúc: 18:33 25/04/2025
#1111 THPT Quốc giaVật lý
Một con lắc đơn gồm dây treo có chiều dài 1,0 m và vật nhỏ có khối lượng 100g mang điện tích Khi vật đang ở vị trí cân bằng, truyền cho vật một vận tốc ban đầu theo phương ngang và có độ lớn m/s. Khi vật đến vị trí biên lần đầu, bật một điện trường đều có vectơ cường độ điện trường cùng hướng và có độ lớn V/m. Lấy g = 10 m/s2. Bỏ qua lực cản của không khí. Kể từ khi bật điện trường, tốc độ cực đại của vật nhỏ đạt được là
Lượt xem: 19,055 Cập nhật lúc: 12:56 26/04/2025
#11818 THPT Quốc giaSinh học
Cho các phát biểu sau về đột biến gen:
I.Trong tự nhiên tần số đột biến của một gen bất kì thường rất thấp.
II.Đột biến gen ở giai đoạn từ 2 đến 8 phôi bào có khả năng truyền lại cho thế hệ sau qua sinh sản hữu tính.
III.Đột biến trong cấu trúc của gen đòi hỏi một số điều kiện nhất định mới biểu hiện trên kiểu hình cơ thể.
IV.Trong quần thể có 3 loại kiểu gen: AA, Aa, aa. Cơ thể mang kiểu gen aa được gọi là thể đột biến
Số phát biểu đúng là:
Lượt xem: 201,058 Cập nhật lúc: 20:51 26/04/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
387 xem13 thi
