Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7933

Cho chóp S.ABCDS . A B C D có đáy là hình thang vuông ABCDA B C D ( ∠BAD=∠ABC=(90)@\angle B A D = \angle A B C = \left(90\right)^{@}), biết BC=AB=aB C = A B = a, AD=2aA D = 2 a. Mặt bên SADS A D là tam giác đều và vuông góc với đáy. Tính bán kính đường tròn ngoại tiếp chóp S.ABCS . A B C.

A.  

a22\dfrac{a \sqrt{2}}{2}.

B.  

a32\dfrac{a \sqrt{3}}{2}.

C.  

a72\dfrac{a \sqrt{7}}{2}.

D.  

a52\dfrac{a \sqrt{5}}{2}.

Đáp án đúng là: D

Cho chóp S.ABCDS . A B C D có đáy là hình thang vuông ABCDA B C D ( ∠BAD=∠ABC=(90)@\angle B A D = \angle A B C = \left(90\right)^{@}), biết BC=AB=aB C = A B = a, AD=2aA D = 2 a. Mặt bên SADS A D là tam giác đều và vuông góc với đáy. Tính bán kính đường tròn ngoại tiếp chóp S.ABCS . A B C.
A. a22\dfrac{a \sqrt{2}}{2}. B. a32\dfrac{a \sqrt{3}}{2}. C. a72\dfrac{a \sqrt{7}}{2}. D. a52\dfrac{a \sqrt{5}}{2}.
Lời giải



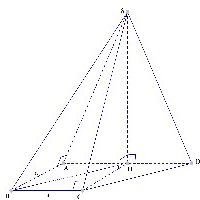
Gọi HH là trung điểm của ADA D. Tam giác SADS A D đều và .
Ta có AH=a, SH=a3A H = a , \textrm{ } S H = a \sqrt{3} và tứ giác ABCHA B C H là hình vuông cạnh aa ⇒BH=a2.\Rightarrow B H = a \sqrt{2} .
Mặt khác hay SAB^=(90)0    (1)\widehat{S A B} = \left(90\right)^{0} \textrm{ }\textrm{ }\textrm{ }\textrm{ } \left( 1 \right).
Chứng minh tương tự ta có BC⊥SCB C \bot S C hay SCB^=(90)0   (2)\widehat{S C B} = \left(90\right)^{0} \textrm{ }\textrm{ }\textrm{ } \left( 2 \right).
Từ (1)\left( 1 \right) và (2)\left( 2 \right) ta thấy hai đỉnh AA và CC của hình chóp S.ABCS . A B C cùng nhìn SBS B dưới một góc vuông. Do đó bốn điểm S,A,B,CS , A , B , C cùng nằm trên mặt cầu đường kính SBS B.
Xét tam giác vuông SHBS H B, ta có SB=BH2+SH2=a5S B = \sqrt{B H^{2} + S H^{2}} = a \sqrt{5}.
Vậy bán kính mặt cầu ngoại tiếp hình chóp S.ABCS . A B C là r=SB2=a52r = \dfrac{S B}{2} = \dfrac{a \sqrt{5}}{2}.


 

Câu hỏi tương tự:

#7721 THPT Quốc giaToán

Cho hình chóp S⋅ABCDS \cdot A B C D có đáy là hình thang vuông tại AA và BB. Biết AB=BC=a,AD=2aA B = B C = a , A D = 2 a. Cạnh bên SAS A vuông góc với mặt phẳng (ABCD)\left( A B C D \right) và SA=a2S A = a \sqrt{2}. Khoảng cách từ BB đến mặt phẳng (SCD)\left( S C D \right) bằng

Lượt xem: 131,333 Cập nhật lúc: 18:40 18/01/2025

#8880 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình vuông, cạnh bên SAS A vuông góc với đáy. Biết rằng AB=a , SD=a5A B = a \textrm{ } , \textrm{ } S D = a \sqrt{5}. Góc giữa đường thẳng ACA C và mặt phẳng (SCD)\left( S C D \right) thuộc khoảng nào dưới đây?

Lượt xem: 151,056 Cập nhật lúc: 18:30 18/01/2025

#8754 THPT Quốc giaToán

Cho chóp S.ABCDS . A B C D có đáy là hình vuông cạnh 2\sqrt{2}, SA=1S A = 1 và vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SBS B và ACA C bằng

Lượt xem: 148,851 Cập nhật lúc: 08:23 17/01/2025

#8302 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình vuông cạnh a3a \sqrt{3}, cạnh bên SD=a6S D = a \sqrt{6} và SDS D vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SDS D và BCB C bằng

Lượt xem: 141,231 Cập nhật lúc: 23:13 18/01/2025

#7730 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh bằng 2\sqrt{2}, cạnh bên SAS A vuông góc với mặt đáy và SA=1S A = 1. Khoảng cách giữa hai đường thẳng SBS B và ACA C bằng

Lượt xem: 131,508 Cập nhật lúc: 23:44 16/01/2025

#8796 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh a,a , cạnh bên SA=a6S A = a \sqrt{6} và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SCS C và mặt phẳng (ABCD)\left( A B C D \right) bằng

Lượt xem: 149,570 Cập nhật lúc: 09:32 17/01/2025

#8504 THPT Quốc giaToán

Cho hình chóp S.ACBDS . A C B D có đáy là hình vuông cạnh aa, SAS A vuông góc với đáy, SA=aS A = a. Khoảng cách giữa hai đường thẳng SBS B và CDC D là

Lượt xem: 144,602 Cập nhật lúc: 23:00 18/01/2025

#7747 THPT Quốc giaToán

Cho hình chóp S.ABC\text{S} . \text{ABC} có đáy ABC\text{ABC} là tam giác đều cạnh a\text{a}, đường thẳng SA\text{SA} vuông góc với mặt phẳng đáy và SA=3a2\text{SA} = \dfrac{3 \text{a}}{2}. Góc giữa hai mặt phẳng và (ABC)\left( \text{ABC} \right) bằng

Lượt xem: 131,739 Cập nhật lúc: 05:45 17/01/2025

#8198 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C Dcó đáy ABCDA B C D là hình chữ nhật có AB=3aA B = 3 a, AD=aA D = a, SAS A vuông góc với mặt phẳng đáy, SA=2aS A = 2 a. Gọi MM là điểm thuộc đoạn thẳng DCD C sao cho DC=3DMD C = 3 D M. Khoảng cách giữa hai đường thẳng BMB M và SDS D bằng

Lượt xem: 139,408 Cập nhật lúc: 23:07 18/01/2025


Đề thi chứa câu hỏi này:

07. Đề thi thử TN THPT môn Toán năm 2024 - THPT CHUYÊN BẮC GIANG - Lần 1.docxTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

5,184 lượt xem 2,737 lượt làm bài