Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8880

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình vuông, cạnh bên SAS A vuông góc với đáy. Biết rằng AB=a , SD=a5A B = a \textrm{ } , \textrm{ } S D = a \sqrt{5}. Góc giữa đường thẳng ACA C và mặt phẳng (SCD)\left( S C D \right) thuộc khoảng nào dưới đây?

A.  

(40∘ ; 60∘)\left( 40 \circ \textrm{ } ; \textrm{ } 60 \circ \right).

B.  

(0∘ ; 20∘)\left( 0 \circ \textrm{ } ; \textrm{ } 20 \circ \right).

C.  

(60∘ ; 80∘)\left( 60 \circ \textrm{ } ; \textrm{ } 80 \circ \right).

D.  

(20∘ ; 40∘)\left( 20 \circ \textrm{ } ; \textrm{ } 40 \circ \right).

Đáp án đúng là: D

Trong (SAD)\left( S A D \right) kẻ AH⊥SD⇒(AC,(SCD))=(AC,CH)=∠ACHA H \bot S D \Rightarrow \left(\right. A C , \left( S C D \right) \left.\right) = \left( A C , C H \right) = \angle A C H
Cách giải:



Trong (SAD)\left( S A D \right) kẻ AH⊥SDA H \bot S D
Do
⇒(AC,(SCD))=(AC,CH)=∠ACH\Rightarrow \left(\right. A C , \left( S C D \right) \left.\right) = \left( A C , C H \right) = \angle A C H
AD=a,SD=a5⇒SA=2aA D = a , S D = a \sqrt{5} \Rightarrow S A = 2 a
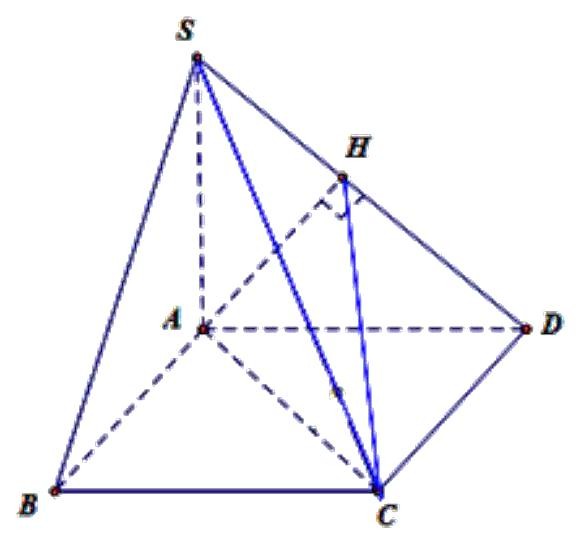
⇒AH=2a5⇒tanACH=AHAC=2a5a2=210⇒∠ACH=32,(31)@\Rightarrow A H = \dfrac{2 a}{\sqrt{5}} \Rightarrow \text{tan} A C H = \dfrac{A H}{A C} = \dfrac{\dfrac{2 a}{\sqrt{5}}}{a \sqrt{2}} = \dfrac{2}{\sqrt{10}} \Rightarrow \angle A C H = 32 , \left(31\right)^{@}
.


 

Câu hỏi tương tự:

#8796 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh a,a , cạnh bên SA=a6S A = a \sqrt{6} và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SCS C và mặt phẳng (ABCD)\left( A B C D \right) bằng

Lượt xem: 149,570 Cập nhật lúc: 09:32 17/01/2025

#8334 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông ABCDA B C D cạnh aa, cạnh bên SAS A vuông góc với mặt phẳng đáy và SA=a2S A = a \sqrt{2}. Thể tích của khối chóp S.ABCDS . A B C D là

Lượt xem: 141,762 Cập nhật lúc: 23:38 16/01/2025

#8302 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình vuông cạnh a3a \sqrt{3}, cạnh bên SD=a6S D = a \sqrt{6} và SDS D vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SDS D và BCB C bằng

Lượt xem: 141,230 Cập nhật lúc: 13:47 16/01/2025

#7730 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh bằng 2\sqrt{2}, cạnh bên SAS A vuông góc với mặt đáy và SA=1S A = 1. Khoảng cách giữa hai đường thẳng SBS B và ACA C bằng

Lượt xem: 131,508 Cập nhật lúc: 23:44 16/01/2025

#7721 THPT Quốc giaToán

Cho hình chóp S⋅ABCDS \cdot A B C D có đáy là hình thang vuông tại AA và BB. Biết AB=BC=a,AD=2aA B = B C = a , A D = 2 a. Cạnh bên SAS A vuông góc với mặt phẳng (ABCD)\left( A B C D \right) và SA=a2S A = a \sqrt{2}. Khoảng cách từ BB đến mặt phẳng (SCD)\left( S C D \right) bằng

Lượt xem: 131,332 Cập nhật lúc: 03:42 16/01/2025

#8011 THPT Quốc giaToán

Cho hình chóp đều S.ABCDS . A B C Dcó đáy ABCDA B C D là hình vuông cạnh bằng

, cạnh bên

.Khoảng cách giữa 2 đường thẳng

và

bằng

Lượt xem: 136,280 Cập nhật lúc: 15:38 16/01/2025

#11369 THPT Quốc giaToán

Cho hình chóp tứ giác S.ABCDS . A B C D có đáy ABCDA B C D là hình vuông cạnh 2a2 a, cạnh bên SAS A vuông góc với mặt phẳng đáy và SA=32aS A = 3 \sqrt{2} a. Tính thể tích khối chóp S.ABCDS . A B C D.

Lượt xem: 193,335 Cập nhật lúc: 03:36 16/01/2025

#11160 THPT Quốc giaToán

Cho hình chóp tứ giác S.ABCDS . A B C D có đáy ABCDA B C D là hình vuông cạnh aa, cạnh bên SAS A vuông góc với mặt phẳng đáy và SA=a5S A = a \sqrt{5}. Thể tích của khối chóp S.ABCDS . A B C D bằng

Lượt xem: 189,785 Cập nhật lúc: 09:53 17/01/2025

#8376 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh aa, mặt bên SABS A B nằm trong mặt phẳng vuông góc với (ABCD)\left( A B C D \right), SAB^=(30)0\widehat{S A B} = \left(30\right)^{0}, SA=2aS A = 2 a. Tính thể tích VV của khối chóp S.ABCD.S . A B C D .

Lượt xem: 142,476 Cập nhật lúc: 01:08 17/01/2025


Đề thi chứa câu hỏi này:

28. Đề thi thử TN THPT môn Toán năm 2024 - THPT Hậu Lộc 4 - Thanh Hóa_rnX62M0d5v.docxTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,884 lượt xem 2,590 lượt làm bài