Cho hàm số bậc ba
. Hàm số
có bảng biến thiên như bên dưới.
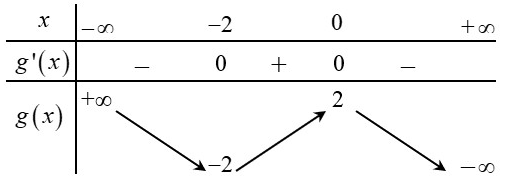
Tổng tất cả các giá trị nguyên của tham số
để tập nghiệm của phương trình
có
phần tử bằng
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: C
Cho hàm số bậc ba
. Hàm số
có bảng biến thiên như bên dưới.

Tổng tất cả các giá trị nguyên của tham số để tập nghiệm của phương trình có phần tử bằng
.
.
.
.
Đáp án đúng là: C
Cho hàm số bậc ba
. Hàm số
có bảng biến thiên như bên dưới.
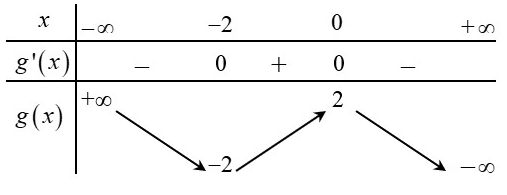
Tổng tất cả các giá trị nguyên của tham số để tập nghiệm của phương trình có phần tử bằng
A. . B. . C. . D. .
Lời giải
Từ gt tìm được có BBT
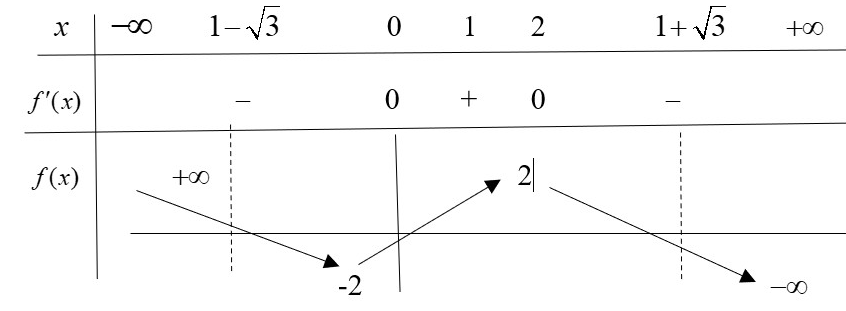
Phương trình , Đk
TH1:
TH2:
Yêu cầu bài toán
TH3:
có đúng 3 nghiệm phân biệt
Nếu không có số nguyên nào thỏa mãn
Nếu (3), (4), (5), mỗi pt 1 nghiệm và nghiệm > 3( không thỏa mãn)
Nên có các giá trị m nguyên là
+) có 1 nghiệm >3( không tm)
có 3 nghiệm pb trong đó có 1 nghiệm >2(KTM)
+)
+)
+)
Vậy hoặc , nên tổng các giá trị của bằng -1, chọn đáp án .
Câu hỏi tương tự:
#8197 THPT Quốc giaToán
Cho hàm số bậc ba
có bảng biến thiên như sau:
Tập hợp tất cả các số thực để phương trình có nghiệm phân biệt trong đó có đúng một nghiệm dương là
Lượt xem: 139,511 Cập nhật lúc: 19:40 14/05/2025
#7775 THPT Quốc giaToán
Cho hàm số bậc ba có đồ thị cắt trục tung tại điểm có tung độ bằng 4,hàm số bậc hai có đồ thị Biết hai đồ thị và cắt nhau tại 3 điểm phân biệt có hoành độ lần lượt là Diện tích hình phẳng giới hạn bởi hai đồ thị và bằng
Lượt xem: 132,372 Cập nhật lúc: 23:05 16/05/2025
#7669 THPT Quốc giaToán
Cho hàm số bậc ba
có đồ thị là đường cong trong hình vẽ. Giá trị cực đại của hàm số đã cho bằng
Lượt xem: 130,520 Cập nhật lúc: 06:32 13/05/2025
#11374 THPT Quốc giaToán
Cho hàm số
có đạo hàm trên
và hàm số
là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.
Hàm số nghịch biến trên
Lượt xem: 193,514 Cập nhật lúc: 08:13 13/05/2025
#7522 THPT Quốc giaToán
Cho hàm số bậc ba
có đồ thị là đường cong đậm trong hình vẽ và đồ thị hàm số
với
có đồ thị là đường cong mảnh như hình vẽ. Đồ thị hàm số
có trục đối xứng là đường thẳng
. Tìm giá trị lớn nhất của hàm số
trên đoạn
.
Lượt xem: 128,008 Cập nhật lúc: 21:49 16/05/2025
#8221 THPT Quốc giaToán
Cho hàm số
có đạo hàm cấp hai liên tục trên
, biết rằng
và hàm số
là hàm số bậc ba có đồ thị như hình vẽ.
Thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi các đồ thị hàm số , khi quay quanh trục có giá trị nằm trong khoảng nào sau đây?
Lượt xem: 139,883 Cập nhật lúc: 21:48 16/05/2025
#8428 THPT Quốc giaToán
Cho
là hàm số bậc ba. Hàm số
có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số
để phương trình
có hai nghiệm thực phân biệt là
Lượt xem: 143,444 Cập nhật lúc: 07:01 14/05/2025
#8564 THPT Quốc giaToán
Cho
là hàm số bậc ba có đồ thị như hình vẽ bên dướiHàm số có bao nhiêu điểm cực trị?
Lượt xem: 145,676 Cập nhật lúc: 16:06 16/05/2025
#8790 THPT Quốc giaToán
Cho hàm số bậc ba
có đồ thị là đường cong trong hình bên
Số điểm cực trị của hàm số là
Lượt xem: 149,536 Cập nhật lúc: 18:13 14/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
418 xem21 thi
