Cho hàm số
bậc bốn có đồ thị như hình vẽ sau:
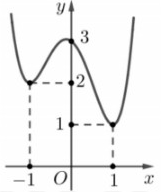
Có bao nhiêu giá trị nguyên của
để hàm số
nghịch biến trên khoảng
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: C
Cho hàm số
bậc bốn có đồ thị như hình vẽ sau:

Có bao nhiêu giá trị nguyên của để hàm số nghịch biến trên khoảng
.
.
.
.
Đáp án đúng là: C
Hàm số
nghịch biến khi
Đặt
Cần tìm điều kiện để
Vậy
có
giá trị nguyên thỏa mãn.
Câu hỏi tương tự:
#7864 THPT Quốc giaToán
Cho hàm số bậc bốn
có đồ thị như hình bên. Hỏi phương trình
có bao nhiêu nghiệm thuộc khoảng
?
Lượt xem: 133,867 Cập nhật lúc: 03:30 17/05/2025
#7650 THPT Quốc giaToán
Cho hàm số bậc bốn
Hàm số
có đồ thị như hình vẽ
Số điểm cực đại của hàm số là
Lượt xem: 130,141 Cập nhật lúc: 16:52 13/05/2025
#7517 THPT Quốc giaToán
Cho
là hàm số đa thức bậc bốn và hàm số
có đồ thị là đường cong như hình dưới đây.
Hàm số có bao nhiêu điểm cực trị thuộc khoảng ?
Lượt xem: 127,890 Cập nhật lúc: 04:10 17/05/2025
#8313 THPT Quốc giaToán
Cho hàm số bậc bốn
có đồ thị là đường cong trong hình dưới đây
Số nghiệm của phương trình là
Lượt xem: 141,435 Cập nhật lúc: 08:14 15/05/2025
#7764 THPT Quốc giaToán
Cho hàm số bậc bốn có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Lượt xem: 132,092 Cập nhật lúc: 22:44 13/05/2025
#8828 THPT Quốc giaToán
Cho hàm số đa thức bậc bốn
thỏa mãn
và đồ thị hàm số
là đường cong trong hình vẽ.
Số điểm cực trị của hàm số là
Lượt xem: 150,223 Cập nhật lúc: 06:33 13/05/2025
#8445 THPT Quốc giaToán
Cho hàm số bậc ba
có đồ thị là đường cong trong hình bên.
Có bao nhiêu giá trị nguyên của tham số để phương trình có ba nghiệm phân biệt
Lượt xem: 143,741 Cập nhật lúc: 02:47 17/05/2025
#8029 THPT Quốc giaToán
Cho hàm số bậc ba
. Hàm số
có bảng biến thiên như bên dưới.
Tổng tất cả các giá trị nguyên của tham số để tập nghiệm của phương trình có phần tử bằng
Lượt xem: 136,596 Cập nhật lúc: 18:10 12/05/2025
#11165 THPT Quốc giaToán
Cho hàm số bậc ba
có đồ thị là đường cong trong hình vẽ dưới đây:
Có bao nhiêu giá trị nguyên của tham số để phương trình có nghiệm thực phân biệt?
Lượt xem: 189,960 Cập nhật lúc: 06:20 15/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
294 xem11 thi
