Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8780

Cho hàm số f(x)=ax4+bx3+cx2,  (a, b, c∈R,a≠0)f \left( x \right) = a x^{4} + b x^{3} + c x^{2} , \textrm{ }\textrm{ } \left( a , \textrm{ } b , \textrm{ } c \in \mathbb{R} , a \neq 0 \right). Hàm số y=f′(x)y = f^{'} \left( x \right) có đồ thị như hình sau:

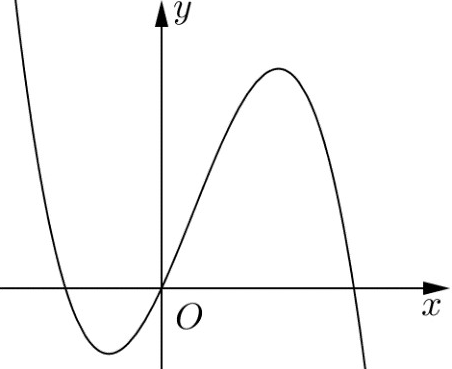
Hình ảnh



Số nghiệm thực phân biệt của phương trình 3f(x)+4=03 f \left( x \right) + 4 = 0 là

A.  

4.

B.  

2.

C.  

3.

D.  

1.

Đáp án đúng là: B

Chọn B
Từ đồ thị của hàm số y=f′(x)y = f^{'} \left( x \right) ta có f′(x)=0⇔[x=0x=m<0x=n>0f^{'} \left( x \right) = 0 \Leftrightarrow \left[\right. x = 0 \\ x = m < 0 \\ x = n > 0 và bảng biến thiên của hàm số f(x)=ax4+bx3+cx2,  (a, b, c∈R)f \left( x \right) = a x^{4} + b x^{3} + c x^{2} , \textrm{ }\textrm{ } \left( a , \textrm{ } b , \textrm{ } c \in \mathbb{R} \right) như sau:



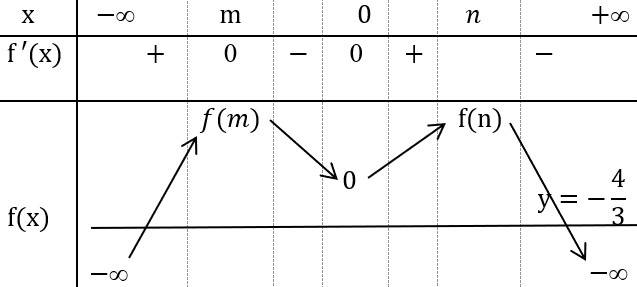
Phương trình 3f(x)+4=0⇔f(x)=−433 f \left( x \right) + 4 = 0 \Leftrightarrow f \left( x \right) = - \dfrac{4}{3}.
Từ bảng biến thiên trên ta có đồ thị hàm số y=f(x)y = f \left( x \right) cắt đường thẳng y=−43y = - \dfrac{4}{3} tại 2 điểm phân biệt.
Vậy phương trình 3f(x)+4=03 f \left( x \right) + 4 = 0 có 2 nghiệm thực phân biệt.


 

Câu hỏi tương tự:

#7575 THPT Quốc giaToán

Cho hàm số y=ax4+bx2+cy = a x^{4} + b x^{2} + c có đồ thị như hình vẽ



Điểm cực đại của đồ thị hàm số đã cho có tọa độ là

Lượt xem: 128,874 Cập nhật lúc: 02:47 23/02/2025

#7650 THPT Quốc giaToán

Cho hàm số bậc bốn f(x).f \left( x \right) . Hàm số y=f′(x)y = f^{'} \left( x \right) có đồ thị như hình vẽ



Số điểm cực đại của hàm số f(x)f \left( x \right) là

Lượt xem: 130,101 Cập nhật lúc: 02:45 23/02/2025

#8859 THPT Quốc giaToán

Cho hàm số y=f(x)=ax4+bx3+cx2+dx+ky = f \left( x \right) = a x^{4} + b x^{3} + c x^{2} + d x + k với a,  b,  c,  d,  k∈Ra , \textrm{ }\textrm{ } b , \textrm{ }\textrm{ } c , \textrm{ }\textrm{ } d , \textrm{ }\textrm{ } k \in \mathbb{R}. Biết hàm số y=f′(x)y = f^{'} \left( x \right) có đồ thị như hình vẽ, đạt cực trị tại điểm O(0;0)O \left( 0 ; 0 \right) và cắt trục hoành tại A(3;0)A \left( 3 ; 0 \right). Có bao nhiêu giá trị nguyên của mm để phương trình f(−x2+2x+m)=kf \left( - x^{2} + 2 x + m \right) = k có hai nghiệm phân biệt?

Lượt xem: 150,659 Cập nhật lúc: 17:40 22/02/2025

#8591 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) có đồ thị f′(x)f^{'} \left( x \right) như hình vẽ



Hàm số g(x)=f(x2)−x63+x4−x2g \left( x \right) = f \left( x^{2} \right) - \dfrac{x^{6}}{3} + x^{4} - x^{2} đồng biến trên khoảng nào dưới đây?

Lượt xem: 146,105 Cập nhật lúc: 06:13 23/02/2025

#7907 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) có đồ thị như hình vẽ bên dưới



Hàm số y=f(x)y = f \left( x \right) nghịch biến trên khoảng nào sau đây?

Lượt xem: 134,476 Cập nhật lúc: 22:26 22/02/2025

#8217 THPT Quốc giaToán

Cho hàm số trùng phương y=(ax)4+bx2+cy = \left(\text{ax}\right)^{4} + b x^{2} + c có đồ thị như hình vẽ.



Hỏi đồ thị hàm số y=(x2−4)(x2+2x)([f(x)])2+2f(x)−3y = \dfrac{\left( x^{2} - 4 \right) \left( x^{2} + 2 x \right)}{\left(\left[\right. f \left( x \right) \left]\right.\right)^{2} + 2 f \left( x \right) - 3} có tổng cộng bao nhiêu tiệm cận đứng?

Lượt xem: 139,856 Cập nhật lúc: 17:03 22/02/2025

#8953 THPT Quốc giaToán

Cho hàm số có đồ thị (C)\left( C \right) và y=mx2+nx+p  (m,n,p∈R)y = m x^{2} + n x + p \textrm{ }\textrm{ } \left( m , n , p \in \mathbb{R} \right) có đồ thị (P)\left( P \right) như hình vẽ. Tính diện tích hình phẳng giới hạn bởi (C)\left( C \right) và (P)\left( P \right) có giá trị nằm trong khoảng nào sau đây?

Lượt xem: 152,297 Cập nhật lúc: 05:25 22/02/2025

#11378 THPT Quốc giaToán

Cho hàm số y=ax+bcx−1y = \dfrac{a x + b}{c x - 1} có đồ thị như hình vẽ bên dưới. Giá trị của tổng S=a+b+cS = a + b + c bằng:


Lượt xem: 193,512 Cập nhật lúc: 12:58 20/02/2025

#7926 THPT Quốc giaToán

Cho hàm số y=ax4+bx2+cy = a x^{4} + b x^{2} + c có đồ thị như hình bên.
OO

−2- 2 −1- 1 11 22
Mệnh đề nào dưới đây đúng?

Lượt xem: 134,858 Cập nhật lúc: 17:26 21/02/2025


Đề thi chứa câu hỏi này:

63. Đề thi thử TN THPT môn Toán năm 2024 - THPT NGUYỄN QUÁN NHO - THANH HÓA - LẦN 3THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,459 lượt xem 2,345 lượt làm bài