Cho hàm số
y = x^{3} + a x^{2} + b x + c \textrm{ }\textrm{ } \left(\right. a , b , c \in \mathbb{R} \right) có đồ thị
và
có đồ thị
như hình vẽ. Tính diện tích hình phẳng giới hạn bởi
và
có giá trị nằm trong khoảng nào sau đây?
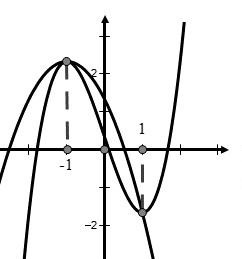
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: B
Cho hàm số
y = x^{3} + a x^{2} + b x + c \textrm{ }\textrm{ } \left(\right. a , b , c \in \mathbb{R} \right) có đồ thị
và
có đồ thị
như hình vẽ. Tính diện tích hình phẳng giới hạn bởi
và
có giá trị nằm trong khoảng nào sau đây?

.
.
.
.
Đáp án đúng là: B
Chọn B
Căn cứ đồ thị ta thấy
+ Hàm số
đạt cực trị tại
nên ta có
.
+ Hàm số
đạt cực đại tại
và
cắt
tại hai điểm có hoành độ
nên ta có
Suy ra
.
Câu hỏi tương tự:
#8338 THPT Quốc giaToán
Cho hàm số có đồ thị và điểm . Gọi là tập hợp tất cả các giá trị thực của để từ kẻ được hai tiếp tuyến đến với là các tiếp điểm và Tổng tất cả các phần tử của bằng
Lượt xem: 141,938 Cập nhật lúc: 21:55 16/05/2025
#8358 THPT Quốc giaToán
Cho hàm số
có đạo hàm liên tục trên
và có đồ thị hàm số
như hình vẽ
Có bao nhiêu giá trị nguyên của để hàm số có 3 điểm cực trị dương?
Lượt xem: 142,259 Cập nhật lúc: 05:22 16/05/2025
#8798 THPT Quốc giaToán
Cho hàm số
có đạo hàm
. Hàm số
liên tục trên tập số thực
và có đồ thị như hình vẽ.
Biết . Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên bằng
Lượt xem: 149,691 Cập nhật lúc: 05:58 16/05/2025
#8336 THPT Quốc giaToán
Cho hàm số
xác định, liên tục trên đoạn
và có đồ thị là đường cong trong hình vẽ.
Hỏi trên đoạn hàm số có bao nhiêu điểm cực trị?
Lượt xem: 141,820 Cập nhật lúc: 22:47 12/05/2025
#7563 THPT Quốc giaToán
Cho hàm số
có
và đồ thị của hàm số
như hình bên dưới
Hỏi hàm số , ( là tham số) có nhiều nhất bao nhiêu điểm cực trị trên nửa khoảng
Lượt xem: 128,736 Cập nhật lúc: 23:48 16/05/2025
#8864 THPT Quốc giaToán
Cho hàm số
có
và đồ thị của hàm số
như hình bên dưới.
Hỏi hàm số , ( là tham số) có nhiều nhất bao nhiêu điểm cực trị trên nửa khoảng ?
Lượt xem: 150,836 Cập nhật lúc: 22:38 16/05/2025
#8568 THPT Quốc giaToán
Cho hai hàm số và có đồ thị lần lượt là . Tổng tất cả các giá trị nguyên thuộc đoạn để cắt tại 4 điểm phân biệt là
Lượt xem: 145,828 Cập nhật lúc: 23:22 16/05/2025
#7522 THPT Quốc giaToán
Cho hàm số bậc ba
có đồ thị là đường cong đậm trong hình vẽ và đồ thị hàm số
với
có đồ thị là đường cong mảnh như hình vẽ. Đồ thị hàm số
có trục đối xứng là đường thẳng
. Tìm giá trị lớn nhất của hàm số
trên đoạn
.
Lượt xem: 128,008 Cập nhật lúc: 21:49 16/05/2025
#8102 THPT Quốc giaToán
Cho hai hàm số
và
có đồ thị như hình vẽ bên.
Khẳng định nào sau đây đúng?
Lượt xem: 138,032 Cập nhật lúc: 18:28 16/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 40 phút
5,362 xem399 thi
