Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8155

Cho hàm số y=f(x)y = f \left( x \right) có đạo hàm f′(x)=2x(x−2)((x+3))5,∀x∈Rf^{'} \left( x \right) = 2 x \left( x - 2 \right) \left(\left( x + 3 \right)\right)^{5} , \forall x \in \mathbb{R}. Số điểm cực tiểu của hàm số đã cho là

A.  

11.

B.  

22.

C.  

33.

D.  

00.

Đáp án đúng là: B

Cho hàm số y=f(x)y = f \left( x \right) có đạo hàm f′(x)=2x(x−2)((x+3))5,∀x∈Rf^{'} \left( x \right) = 2 x \left( x - 2 \right) \left(\left( x + 3 \right)\right)^{5} , \forall x \in \mathbb{R}. Số điểm cực tiểu của hàm số đã cho là
A. 11. B. 22. C. 33. D. 00.
Lời giải
Giải f′(x)=0⇔2x(x−2)((x+3))5=0⇔[x=0x=2x=−3f^{'} \left( x \right) = 0 \Leftrightarrow 2 x \left( x - 2 \right) \left(\left( x + 3 \right)\right)^{5} = 0 \Leftrightarrow \left[\right. x = 0 \\ x = 2 \\ x = - 3.
Bảng biến thiên:


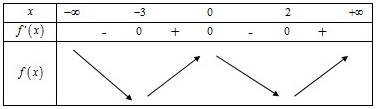
Hàm số y=f(x)y = f \left( x \right) có 22 điểm cực tiểu.


 

Câu hỏi tương tự:

#7616 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) có đạo hàm f′(x)=x(x−1)(x+2())3f^{'} \left( x \right) = x \left( x - 1 \right) \left( x + 2 \left(\right)\right)^{3}, ∀x∈R\forall x \in R. Số điểm cực tiểu của hàm số đã cho là

Lượt xem: 129,613 Cập nhật lúc: 02:44 27/04/2025

#7746 THPT Quốc giaToán

Cho hàm số f(x)\text{f} \left( \text{x} \right) có đạo hàm (f)′(x)=(x−1())2(x−3())3\left(\text{f}\right)^{'} \left( \text{x} \right) = \left( \text{x} - 1 \left(\right)\right)^{2} \left( \text{x} - 3 \left(\right)\right)^{3}. Số điểm cực trị của hàm số đã cho bằng

Lượt xem: 131,816 Cập nhật lúc: 00:23 27/04/2025

#8984 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) có đạo hàm f′(x)=x(x+1)(x−4)3,   ∀x∈Rf^{'} \left( x \right) = x \left( x + 1 \right) \left( x - 4 \right)^{3} , \textrm{ }\textrm{ }\textrm{ } \forall x \in \mathbb{R}. Số điểm cực đại của hàm số đã cho là

Lượt xem: 152,858 Cập nhật lúc: 15:54 26/04/2025

#7911 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) có đạo hàm f′(x)=x(x−1)(x−2())2(x2−1),∀x∈Rf^{'} \left( x \right) = x \left( x - 1 \right) \left( x - 2 \left(\right)\right)^{2} \left( x^{2} - 1 \right) , \forall x \in \mathbb{R}. Số điểm cực trị của hàm số đã cho là

Lượt xem: 134,555 Cập nhật lúc: 20:21 23/04/2025

#8298 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) có đạo hàm f′(x)=x(x+2())2,∀x∈Rf^{'} \left( x \right) = x \left( x + 2 \left(\right)\right)^{2} , \forall x \in \mathbb{R}. Tìm số điểm cực trị của hàm số đã cho.

Lượt xem: 141,227 Cập nhật lúc: 20:24 26/04/2025

#7947 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right)có đạo hàm là f′(x)=x(x−1)(x+2)2 ∀x∈Rf^{'} \left( x \right) = x \left( x - 1 \right) \left( x + 2 \right)^{2} \textrm{ } \forall x \in \mathbb{R}. Số điểm cực trị của hàm số là?

Lượt xem: 135,251 Cập nhật lúc: 20:23 26/04/2025

#7523 THPT Quốc giaToán

Cho hàm số có đạo hàm là f′(x)=x((x−1))2((x−2))3f^{'} \left( x \right) = x \left(\left( x - 1 \right)\right)^{2} \left(\left( x - 2 \right)\right)^{3}. Số điểm cực trị của hàm số đã cho là

Lượt xem: 127,965 Cập nhật lúc: 18:20 24/04/2025

#7997 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) có đạo hàm f′(x)=(2x+1)(x+2)2(3x−1)4, ∀x∈R.f^{'} \left( x \right) = \left( 2 x + 1 \right) \left( x + 2 \right)^{2} \left( 3 x - 1 \right)^{4} , \textrm{ } \forall x \in \mathbb{R} . Số điểm cực trị của đồ thị hàm số f(x)f \left( x \right) là

Lượt xem: 136,108 Cập nhật lúc: 15:42 26/04/2025

#7881 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) có đạo hàm f′(x)=2024(x−1)(x2−3)(x4−1)∀x∈R.f^{'} \left( x \right) = 2024 \left( x - 1 \right) \left( x^{2} - 3 \right) \left( x^{4} - 1 \right) \forall x \in R .Số điểm cực trị của hàm số y=f(x)y = f \left( x \right) là

Lượt xem: 134,121 Cập nhật lúc: 15:42 26/04/2025


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - THPT TRẦN PHÚ - HẢI PHÒNG

1 mã đề 50 câu hỏi 1 giờ 30 phút

897 xem61 thi