Cho hàm số
có đạo hàm
với mọi
. Hàm số đã cho nghịch biến trên khoảng nào?
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: A
Cho hàm số có đạo hàm với mọi . Hàm số đã cho nghịch biến trên khoảng nào?
.
.
.
.
Đáp án đúng là: A
Cho hàm số
có đạo hàm
với mọi
. Hàm số đã cho nghịch biến trên khoảng nào?
A.
. B.
. C.
. D.
.
Lời giải
Ta có
.
Bảng xét dấu
:
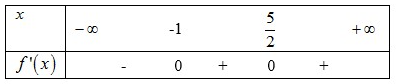
Vậy hàm số nghịch biến trên khoảng .
Câu hỏi tương tự:
#7535 THPT Quốc giaToán
Cho hàm số có đạo hàm với mọi . Hàm số có bao nhiêu điểm cực đại?
Lượt xem: 128,257 Cập nhật lúc: 04:20 17/05/2025
#7598 THPT Quốc giaToán
Cho hàm số có đạo hàm với mọi . Có bao nhiêu số nguyên dương để hàm số đồng biến trên khoảng ?
Lượt xem: 129,337 Cập nhật lúc: 02:01 17/05/2025
#7888 THPT Quốc giaToán
Cho hàm số có đạo hàm với mọi . Có bao nhiêu giá trị nguyên dương của tham số để hàm số có đúng điểm cực trị?
Lượt xem: 134,194 Cập nhật lúc: 04:25 17/05/2025
#8784 THPT Quốc giaToán
Cho hàm số có đạo hàm trên và thỏa mãn với mọi . Biết , giá trị của bằng
Lượt xem: 149,504 Cập nhật lúc: 02:38 17/05/2025
#8307 THPT Quốc giaToán
Cho hàm số có đạo hàm trên thỏa mãn và mọi . Biết với . Giá trị của biểu thức bằng
Lượt xem: 141,394 Cập nhật lúc: 16:19 13/05/2025
#8496 THPT Quốc giaToán
Cho hàm số
có đạo hàm với . Có bao nhiêu giá trị nguyên của tham số để hàm số có 4 điểm cực trị?Lượt xem: 144,524 Cập nhật lúc: 04:15 17/05/2025
#11176 THPT Quốc giaToán
Cho hàm số có đạo hàm liên tục trên và thỏa mãn . Biết diện tích hình phẳng giới hạn bởi đồ thị các hàm số và và ( với và là phân số tối giản). Khi đó giá trị của hiệu bằng
Lượt xem: 190,093 Cập nhật lúc: 00:18 17/05/2025
#7521 THPT Quốc giaToán
Cho hàm số có đạo hàm trên . Nếu hàm số đã cho có đúng hai điểm cực trị là – 1 và 2 thì hàm số có tất cả bao nhiêu điểm cực trị?
Lượt xem: 127,947 Cập nhật lúc: 17:59 10/05/2025
#8987 THPT Quốc giaToán
Cho hàm số có đạo hàm là . Có bao nhiêu giá trị nguyên của tham số để hàm số có đúng 9 điểm cực trị?
Lượt xem: 152,990 Cập nhật lúc: 02:51 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
1,469 xem98 thi
