Cho hàm số $y = f \left( x \right)$ có đạo hàm là $f^{'} \left( x \right) = x^{2} + 10 x , \forall x \in \mathbb{R}$. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = f \left( x^{4} - 8 x^{2} + m \right)$ có đúng 9 điểm cực trị?

A.  

16.

B.  

9.

C.  

15.

D.  

10.

Đáp án đúng là: D

Ta có  $f'(x) = x^{2} + 10x = 0 \Leftrightarrow \begin{cases} x = 0 \\ x = -10 \end{cases}$
Ta có  $y' = (4x^{3} - 16x) f'(x^{4} - 8x^{2} + m) = 0 \Leftrightarrow \begin{cases} 4x^{3} - 16x = 0 \\ f'(x^{4} - 8x^{2} + m) = 0 \end{cases} \Leftrightarrow \begin{cases} x = -2 \\ x = 0 \\ x = 2 \\ x^{4} - 8x^{2} + m = 0 \\ x^{4} - 8x^{2} + m + 10 = 0 \end{cases}$
Xét hàm số  $g(x) = x^{4} - 8x^{2}$ trên  $\mathbb{R}$.
Ta có  $g'(x) = 4x^{3} - 16x = 0 \Leftrightarrow \begin{cases} x = -2 \\ x = 0 \\ x = 2 \end{cases}$.
Bảng biến thiên
 

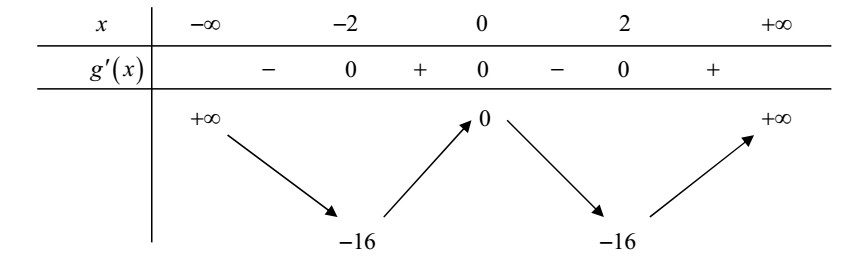
Vì  $-10 - m < -m$ nên để hàm số đã cho có 9 điểm cực trị thì  $\begin{cases} -16 < -m - 10 < 0 \\ 0 \leq -m \end{cases}$ 
$\Leftrightarrow -10 < m \leq 0$. Mà  $m \in \mathbb{Z}$ nên  $m \in \{-9, -8, ..., -1, 0\}$. Vậy có 10 giá trị thỏa mãn.