Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7694

Cho hình chóp S.ABCDS . A B C Dcó đáy là hình vuông ABCDA B C Dtâm OO, SA=2a2S A = 2 a \sqrt{2}. Hình chiếu vuông góc của SSlên mặt phẳng (ABCD)\left( A B C D \right)trùng với trung điểm của cạnh OAO A, biết tam giác SBDS B Dvuông tại S. Khoảng cách từ điểm DDđến mặt phẳng (SBC)\left( S B C \right)bằng

A.  

3a510\dfrac{3 a \sqrt{5}}{10}.

B.  

2a55\dfrac{2 a \sqrt{5}}{5}.

C.  

4a105\dfrac{4 a \sqrt{10}}{5}.

D.  

2a105\dfrac{2 a \sqrt{10}}{5}.

Đáp án đúng là: C

Cho hình chóp S.ABCDS . A B C Dcó đáy là hình vuông ABCDA B C Dtâm OO, SA=2a2S A = 2 a \sqrt{2}. Hình chiếu vuông góc của SSlên mặt phẳng (ABCD)\left( A B C D \right)trùng với trung điểm của cạnh OAO A, biết tam giác SBDS B Dvuông tại S. Khoảng cách từ điểm DDđến mặt phẳng (SBC)\left( S B C \right)bằng
A. 3a510\dfrac{3 a \sqrt{5}}{10}. B. 2a55\dfrac{2 a \sqrt{5}}{5}. C. 4a105\dfrac{4 a \sqrt{10}}{5}. D. 2a105\dfrac{2 a \sqrt{10}}{5}.
Lời giải



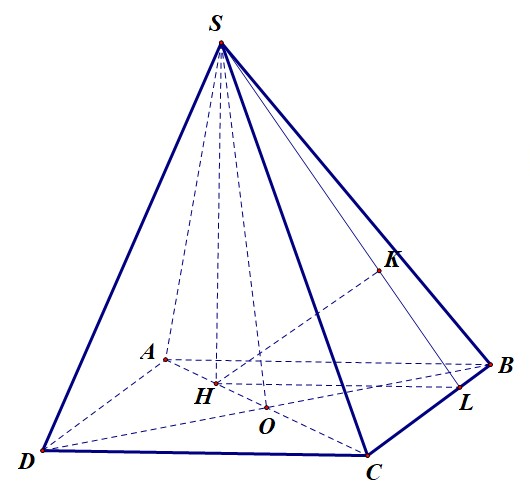
Gọi HHlà trung điểm của OAO A.
Qua HHvẽ đường thẳng song song với ABA B cắt BCB C tại LL.
Trong (SHL)\left( S H L \right) vẽ HKH K vuông góc với SLS L.

Ta có: ΔSHD=ΔSHB(cgc−cgc)\Delta S H D = \Delta S H B \left( c g c - c g c \right), suy ra ΔSBD\Delta S B Dvuông cân tại SS.
Lại có: HH là trung điểm của OAO A và SH⊥OAS H \bot O A ( Vì: SH⊥(ABCD)S H \bot \left( A B C D \right)).
Do đó ΔSAO\Delta S A O cân tại SS.
Suy ra: SA=SO=OB=OD=2a2S A = S O = O B = O D = 2 a \sqrt{2} nên: BD=4a2=AC⇒AH=a2B D = 4 a \sqrt{2} = A C \Rightarrow A H = a \sqrt{2}
Vậy, cạnh của hình vuông có AD=DC=AB=BC=4aA D = D C = A B = B C = 4 a và SH=SO2−HO2=a6S H = \sqrt{S O^{2} - H O^{2}} = a \sqrt{6}
Mặt khác:
HL//AB⇒CHAC=HLAB=34⇒d(H,(SBC))=34d(A,(SBC))=34d(D,(SBC))H L / / A B \Rightarrow \dfrac{C H}{A C} = \dfrac{H L}{A B} = \dfrac{3}{4} \\ \Rightarrow d \left(\right. H , \left( S B C \right) \left.\right) = \dfrac{3}{4} d \left(\right. A , \left( S B C \right) \left.\right) = \dfrac{3}{4} d \left(\right. D , \left( S B C \right) \left.\right)
d(H,(SBC))=HP=11SH2+1HL2=3a105⇒d(D,(SBC))=4a105d \left(\right. H , \left( S B C \right) \left.\right) = H P = \sqrt{\dfrac{1}{\dfrac{1}{S H^{2}} + \dfrac{1}{H L^{2}}}} = \dfrac{3 a \sqrt{10}}{5} \\ \Rightarrow d \left(\right. D , \left( S B C \right) \left.\right) = \dfrac{4 a \sqrt{10}}{5}


 

Câu hỏi tương tự:

#8662 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy là tam giác vuông tại AA, AB=6aA B = 6 a, AC=4aA C = 4 a, SAS A vuông góc với mặt
phẳng đáy và SA=aS A = a. Gọi MM là trung điểm của ABA B. Khoảng cách giữa hai đường thẳng SMS M và
BCB C bằng

Lượt xem: 147,286 Cập nhật lúc: 03:20 22/11/2024

#8028 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy là tam giác vuông tại AA và AB=3A B = \sqrt{3}, AC=7A C = \sqrt{7}, SA=1S A = 1. Hai mặt bên (SAB)\left( S A B \right) và (SAC)\left( S A C \right) lần lượt tạo với mặt đáy các góc bằng 45∘45 \circ và 60∘60 \circ. Thể tích của khối chóp đã cho bằng

Lượt xem: 136,509 Cập nhật lúc: 07:32 22/11/2024

#7976 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy ABCA B C là tam giác vuông cân tại B,B , AB=2aA B = 2 a và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ CC đến mặt phẳng (SAB)\left( S A B \right) bằng

Lượt xem: 135,623 Cập nhật lúc: 07:46 22/11/2024

#8523 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy ABCA B C là tam giác vuông tại BB và cạnh bên SAS A vuông góc với đáy. Gọi MM là trung điểm của SC,S C , biết AB=a,  AC=2a,  SA=a3.A B = a , \textrm{ }\textrm{ } A C = 2 a , \textrm{ }\textrm{ } S A = a \sqrt{3} . Tính thể tích khối chóp S.AMBS . A M B theo a.a .

Lượt xem: 144,954 Cập nhật lúc: 09:01 22/11/2024

#8431 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy là tam giác vuông cân tại A.A . Biết AB=aA B = a, SAS A vuông góc với đáy và SBS B tạo với đáy góc (45)@\left(45\right)^{@}. Tính khoảng cách từ AA đến mặt phẳng .

Lượt xem: 143,390 Cập nhật lúc: 09:16 22/11/2024

#8184 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy ABCA B C là tam giác vuông tại AA, AB=aA B = a, AC=a2A C = a \sqrt{2}. Biết thể tích khối chóp S.ABCS . A B C bằng a32\dfrac{a^{3}}{2}. Khoảng cách từ SS đến mặt phẳng (ABC)\left( A B C \right) bằng

Lượt xem: 139,154 Cập nhật lúc: 09:17 22/11/2024

#8552 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy ABCA B C là tam giác vuông tại AA; AB=3aA B = 3 a, AC=aA C = a và đường cao SA=2aS A = 2 a. Thể tích khối chóp S.ABCS . A B C bằng

Lượt xem: 145,410 Cập nhật lúc: 09:23 22/11/2024

#8034 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C Dcó đáy ABCDA B C D là hình vuông tâm OO. Tam giác SABS A B là tam giác vuông tại SS và nằm trong mặt phẳng vuông góc với đáy. Tâm mặt cầu ngoại tiếp hình chóp S.ABCS . A B C là

Lượt xem: 136,637 Cập nhật lúc: 09:30 22/11/2024

#8571 THPT Quốc giaToán

Cho hình chớp S.ABCS . A B C có đáy là tam giác đều cạnh a,SAa , S A vuông góc mặt phẳng đáy, SB=3aS B = \sqrt{3} a (tham khảo hình vẽ)



Khoảng cách từ trung điểm MM của SAS A đến mặt phẳng (SBC)\left( S B C \right) bằng

Lượt xem: 145,731 Cập nhật lúc: 11:19 07/11/2024


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN -THPT-YÊN-LẠC-LẦN-3 THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

1,347 lượt xem 693 lượt làm bài