Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình bình hành. Mặt bên $S A D$ là tam giác đều cạnh $a \sqrt{3}$ . $A C D$ là tam giác vuông tại $A$ có cạnh $A C = a$ , góc giữa đường thẳng $A B$ và mặt phẳng $\left( S A D \right)$ bằng $\left(60\right)^{0}$ . Thể tích khối chóp $S . A B C D$ bằng
A.
$a^{3}$ .
B.
$\dfrac{\sqrt{3} a^{3}}{2}$ .
C.
$\dfrac{3 a^{3}}{4}$ .
D.
$\dfrac{3 a^{3}}{2}$ .
Đáp án đúng là: D

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình bình hành. Mặt bên $S A D$ là tam giác đều cạnh $a \sqrt{3}$ . $A C D$ là tam giác vuông tại $A$ có cạnh $A C = a$ , góc giữa đường thẳng $A B$ và mặt phẳng $\left( S A D \right)$ bằng $\left(60\right)^{0}$ . Thể tích khối chóp $S . A B C D$ bằng
A. $a^{3}$ . B. $\dfrac{\sqrt{3} a^{3}}{2}$ . C. $\dfrac{3 a^{3}}{4}$ . D. $\dfrac{3 a^{3}}{2}$ .
Lời giải

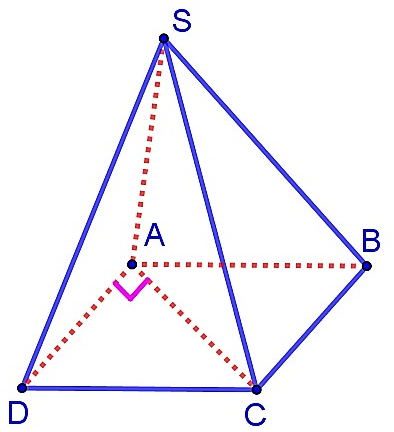
Xét tam giác vuông

A C D

có

C D = \sqrt{A D^{2} + A C^{2}} = \sqrt{\left(\left( a \sqrt{3} \right)\right)^{2} + a^{2}} = 2 a \Rightarrow A B = 2 a

.
Ta có

d \left(\right. B , \textrm{ } \left( S A D \right) \left.\right) = A B . sin60 \circ = a \sqrt{3}

.
Ta có

V_{S . A B D} = V_{B . \textrm{ } S A D} = \dfrac{1}{3} . S_{\Delta S A D} . d \left(\right. B ; \textrm{ } \left( S A D \right) \left.\right) = \dfrac{1}{3} . \dfrac{\left(\left( a \sqrt{3} \right)\right)^{2} \sqrt{3}}{4} . a \sqrt{3} = \dfrac{3 a^{3}}{4}

.
Ta có

V_{S . A B C D} = 2 . V_{S . A B D} = \dfrac{3 a^{3}}{2}

Câu hỏi tương tự:

#7866 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy là hình bình hành và $S A = S B = S C = a$ , hình chiếu vuông góc của $S$ lên mặt phẳng $A B C D$ thuộc đoạn $A C$ (không trùng với $A , C$ ). Giá trị lớn nhất của thể tích khối chóp $S . A B C D$ là:

Lượt xem: 133,818 Cập nhật lúc: 09:23 17/01/2025

#8566 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình bình hành. Goi $M$ là trung điem cua cạnh $S A$ . Mặt phȁng $\left( \alpha \right)$ đi qua $M$ và song song với mặt phȁng $\left( S B C \right)$ chia khối chóp $S . A B C D$ thành hai phần. Tính tỉ số của thể tích phần chứa đỉnh $S$ và thể tích phần còn lại.

Lượt xem: 145,662 Cập nhật lúc: 11:02 18/01/2025

#8304 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình bình hành, trên cạnh $S A$ lấy điểm $M$ và đặt $\dfrac{S M}{S A} = x$ . Giá trị $x$ để mặt phẳng $\left( M B C \right)$ chia khối chóp đã cho thành hai phần có thể tích bằng nhau là:

Lượt xem: 141,267 Cập nhật lúc: 18:20 18/01/2025

#8944 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy $\text{ABCD}$ là hình bình hành. Gọi $M$ là trung điểm cạnh $\text{AD}$ . Gọi $V_{1} , V_{2}$ lần lượt là thể tích của hai khối chóp $S . A B M$ và $S . A B C$ thì $\dfrac{V_{1}}{V_{2}}$ bằng

Lượt xem: 152,091 Cập nhật lúc: 18:30 18/01/2025

#8449 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình bình hành. Hai điểm $M , \textrm{ }\textrm{ } N$ lần lượt thuộc các đoạn thẳng $A B$ và $A D$ (M và N không trùng với A) sao cho $\dfrac{2 A B}{A M} + \dfrac{3 A D}{A N} = 8$ . Kí hiệu $V , \textrm{ }\textrm{ } V_{1}$ lần lượt là thể tích của các khối chóp $S . A B C D$ và $S . M B D N .$ Giá trị lớn nhất của tỉ số $\dfrac{V_{1}}{V}$ bằng

Lượt xem: 143,721 Cập nhật lúc: 06:40 16/01/2025

#8615 THPT Quốc giaToán

Cho khối chóp $S . A B C D$ có đáy là hình bình hành tâm $O$ , biết thể tích khối chóp $S . O A D$ bằng $10 c m^{3}$ . Thể tích khối chóp $S . A B C D$ bằng?

Lượt xem: 146,551 Cập nhật lúc: 18:20 18/01/2025

#8923 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình vuông cạnh $a$ . Biết $S A \bot \left( A B C D \right)$ và $S A = a \sqrt{3}$ . Thể tích của khối chóp $S . A B C D$ là:

Lượt xem: 151,790 Cập nhật lúc: 18:28 18/01/2025

#7524 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy là hình vuông cạnh $a , S A = 2 a$ và $S A$ vuông góc với đáy. Tính theo $a$ khoảng cách từ $A$ đến mặt phẳng $\left( S B D \right)$ .

Lượt xem: 128,005 Cập nhật lúc: 18:26 18/01/2025

#8880 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình vuông, cạnh bên $S A$ vuông góc với đáy. Biết rằng $A B = a \textrm{ } , \textrm{ } S D = a \sqrt{5}$ . Góc giữa đường thẳng $A C$ và mặt phẳng $\left( S C D \right)$ thuộc khoảng nào dưới đây?

Lượt xem: 151,056 Cập nhật lúc: 18:30 18/01/2025

Đề thi chứa câu hỏi này:

Đề thi thử Tốt nghiệp THPT Môn Toán 2023 - SỞ GD SƠN LA THPT Quốc giaToán

1 mã đề 50 câu hỏi 50 phút

1,513 lượt xem 763 lượt làm bài

LetQA - Nền tảng trắc nghiệm & đề thi đa lĩnh vực

Về chúng tôi

LetQA là công cụ hỗ trợ học sinh, sinh viên, giáo viên, tổ chức trong việc ôn luyện, kiểm tra kiến thức; được cung cấp miễn phí cho tất cả người dùng.
LetQA không cung cấp dịch vụ mạng xã hội, không cung cấp thông tin tổng hợp và không thu phí người dùng.

Thông tin liên hệ & hỗ trợ

Email: hotro@letqa.com

Facebook: Let QA (fb.com/letqavn)

Liên kết phổ biến

Yêu cầu bổ sung đề thi

Đóng góp đề thi

Website liên kết

Phần mềm kiểm tra trùng lặp Kiểm Tra Tài Liệu

Phần mềm xuất bản tạp chí điện tử VOJS

Công cụ kiểm tra chính tả và thể thức Viver

Công cụ hỗ trợ trích dẫn và phân tích khoa học Scholar Hub