Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7609

Cho hình nón có thiết diện qua đỉnh là tam giác SABS A B vuông tại SS, ( A, BA , \textrm{ } B thuộc đường tròn đáy). Biết tam giác SABS A B có bán kính đường tròn nội tiếp bằng 25−102 \sqrt{5} - \sqrt{10}, đường cao SOS O tạo với mặt phẳng \left(\right. S A B \right) một góc 30∘30 \circ. Diện tích xung quanh của hình nón đã cho bằng

A.  

510π5 \sqrt{10} \pi.

B.  

415π4 \sqrt{15} \pi.

C.  

52π5 \sqrt{2} \pi.

D.  

25π2 \sqrt{5} \pi.

Đáp án đúng là: A

Cho hình nón có thiết diện qua đỉnh là tam giác SABS A B vuông tại SS, ( A, BA , \textrm{ } B thuộc đường tròn đáy). Biết tam giác SABS A B có bán kính đường tròn nội tiếp bằng 25−102 \sqrt{5} - \sqrt{10}, đường cao SOS O tạo với mặt phẳng (SAB)\left( S A B \right) một góc 30∘30 \circ. Diện tích xung quanh của hình nón đã cho bằng
A. 510π5 \sqrt{10} \pi. B. 415π4 \sqrt{15} \pi. C. 52π5 \sqrt{2} \pi. D. 25π2 \sqrt{5} \pi.
Lời giải



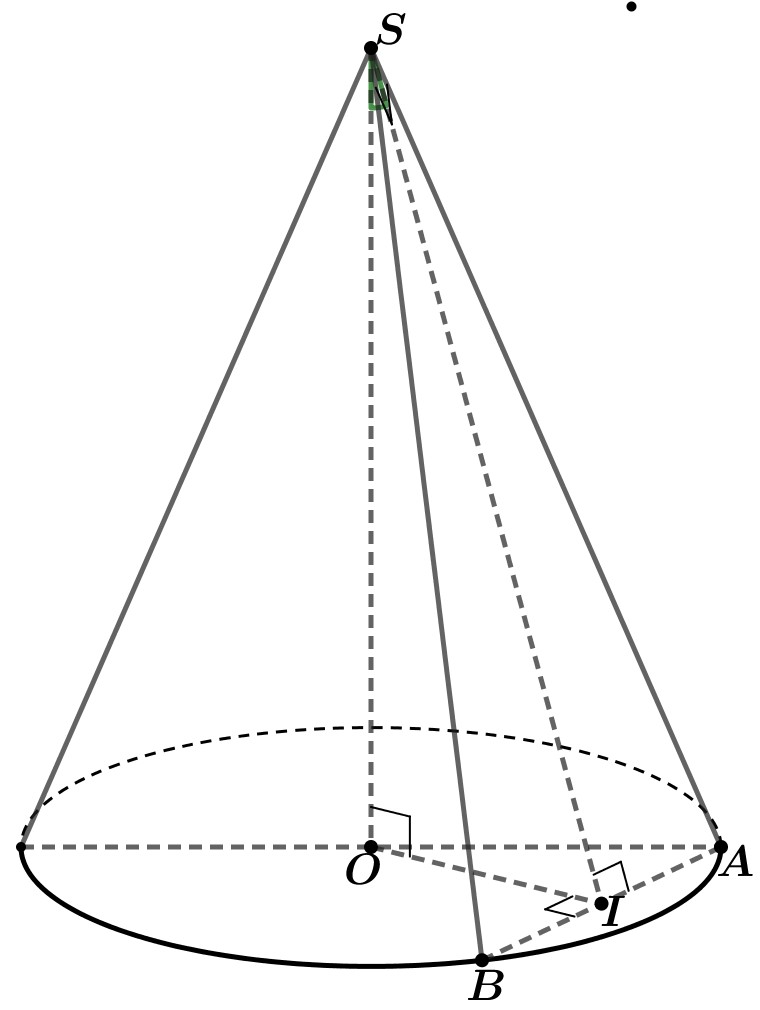
Kẻ OI⊥AB⇒ ISO^=30∘O I \bot A B \Rightarrow \textrm{ } \hat{I S O} = 30 \circ.
Ta có: SSAB=p.r⇔ 12l2=2l+2 l2.(25−10)⇒ l=25S_{S A B} = p . r \Leftrightarrow \textrm{ } \dfrac{1}{2} l^{2} = \dfrac{2 l + \sqrt{2} \textrm{ } l}{2} . \left( 2 \sqrt{5} - \sqrt{10} \right) \Rightarrow \textrm{ } l = 2 \sqrt{5}. Từ đó suy ra: AB=210,A B = 2 \sqrt{10} , SI=10S I = \sqrt{10}, SO=302S O = \dfrac{\sqrt{30}}{2} và R=OA=522R = O A = \dfrac{5 \sqrt{2}}{2}.
Vậy diện tích xung quanh: Sxq=πrl=510πS_{\text{xq}} = \pi r l = 5 \sqrt{10} \pi.
HẾT


 

Câu hỏi tương tự:

#8189 THPT Quốc giaToán

Cho hình nón (N)\left( N \right) có đỉnh SS, chiều cao h=3h = 3. Mặt phẳng (P)\left( P \right) qua đỉnh SS cắt hình nón (N)\left( N \right)theo thiết diện là tam giác đều. Khoảng cách từ tâm đáy hình nón đến mặt phẳng (P)\left( P \right) bằng 6\sqrt{6}. Thể tích khối nón giới hạn bởi hình nón (N)\left( N \right) bằng

Lượt xem: 139,256 Cập nhật lúc: 03:29 24/11/2024

#8749 THPT Quốc giaToán

Cho hình nón có chiều cao

, bán kính đáy

. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là

. Tính diện tích

của thiết diện đó.

Lượt xem: 148,780 Cập nhật lúc: 13:09 23/11/2024

#8101 THPT Quốc giaToán

Cho hình nón tròn xoay có chiều cao bằng 44và bán kính đáy bằng 33. Mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là một tam giác cân có độ dài cạnh đáy bằng 22. Diện tích của thiết diện bằng:

Lượt xem: 137,784 Cập nhật lúc: 02:06 23/11/2024

#8326 THPT Quốc giaToán

Cho hình nón tròn xoay có chiều cao bằng 2a2 a, bán kính đáy bằng 3a3 a. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện bằng 3a2\dfrac{3 a}{2}. Diện tích của thiết diện đó bằng

Lượt xem: 141,572 Cập nhật lúc: 19:31 24/11/2024

#8004 THPT Quốc giaToán

Cho có tháp nước như hình dưới đây, tháp được thiết kế gồm thân tháp có dạng hình trụ, phần mái phía trên dạng hình nón và đáy là nửa hình cầu. Không gian bên trong toàn bộ tháp được minh họa theo hình vẽ với đường kính đáy hình trụ, hình cầu và đường kính đáy của hình nón đều bằng 3m, chiều cao hình trụ là 2m, chiều cao của hình nón là 1m.



Thể tích của toán bộ không gian bên trong tháp nước gần nhất với giá trị nào sau đây?

Lượt xem: 136,092 Cập nhật lúc: 12:33 24/11/2024

#8360 THPT Quốc giaToán

Cho hình nón có bán kính đáy bằng 3 chiều cao bằng 6, một khối trụ có bán kính đáy thay đổi nội tiếp khối nón đã cho (như hình vẽ). Khi thể tích khối trụ đạt giá trị lớn nhất thì diện tích toàn phần của hình trụ bằng

Lượt xem: 142,154 Cập nhật lúc: 17:26 24/11/2024

#8843 THPT Quốc giaToán

Cho hình nón có bán kính đáy bằng 4, chiều cao bằng 8. Một khối trụ có bán kính đáy thay đổi và nội tiếp hình nón đã cho (tham khảo hình vẽ). Thể tích của khối trụ đạt giá trị lớn nhất bằng

Lượt xem: 150,394 Cập nhật lúc: 03:11 24/11/2024

#7660 THPT Quốc giaToán

Cho hình nón có diện tích xung quanh bằng 8π8 \pi và độ dài đường sinh là 44. Tính bán kính đường tròn đáy của hình nón.

Lượt xem: 130,282 Cập nhật lúc: 12:36 23/11/2024

#7559 THPT Quốc giaToán

Cho hình nón có chiều cao bằng 8 cm8 \textrm{ } \text{cm}, bán kính đáy bằng 6 cm6 \textrm{ } \text{cm}. Diện tích toàn phần của hình nón đã cho bằng

Lượt xem: 128,563 Cập nhật lúc: 06:05 23/11/2024


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - SỞ PHÚ THỌTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

696 lượt xem 350 lượt làm bài