Cho hình nón
có đỉnh
, chiều cao
. Mặt phẳng
qua đỉnh
cắt hình nón
theo thiết diện là tam giác đều. Khoảng cách từ tâm đáy hình nón đến mặt phẳng
bằng
. Thể tích khối nón giới hạn bởi hình nón
bằng
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: D
Cho hình nón có đỉnh , chiều cao . Mặt phẳng qua đỉnh cắt hình nón theo thiết diện là tam giác đều. Khoảng cách từ tâm đáy hình nón đến mặt phẳng bằng . Thể tích khối nón giới hạn bởi hình nón bằng
.
.
.
.
Đáp án đúng là: D
Cho hình nón
có đỉnh
, chiều cao
. Mặt phẳng
qua đỉnh
cắt hình nón
theo thiết diện là tam giác đều. Khoảng cách từ tâm đáy hình nón đến mặt phẳng
bằng
. Thể tích khối nón giới hạn bởi hình nón
bằng
A.
. B.
. C.
. D.
.
Lời giải
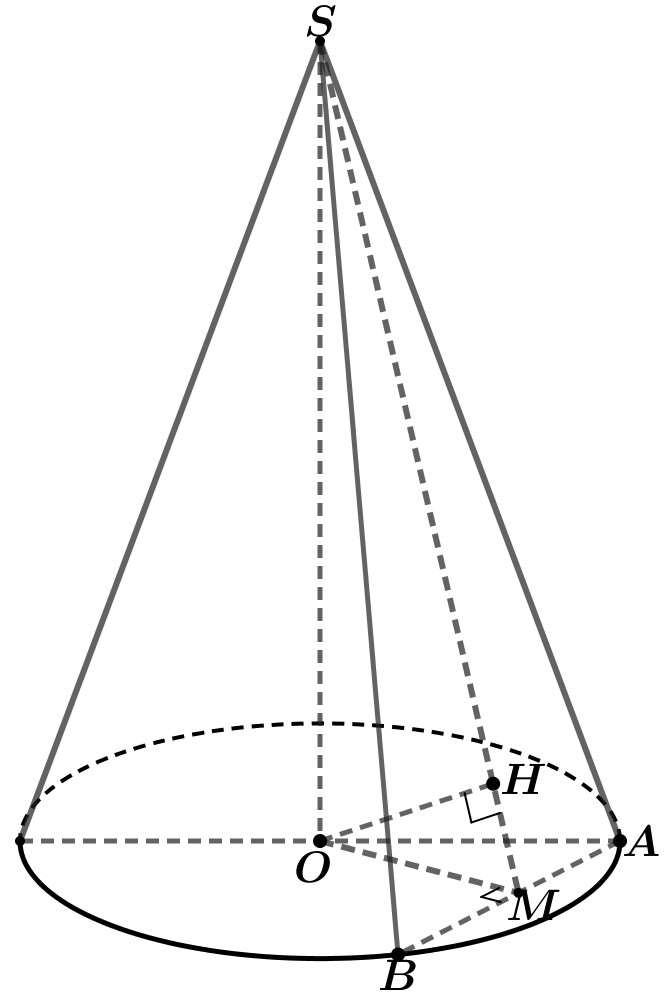
Kẻ và . Ta suy ra .
Ta có: và , .
Vậy thể tích khối nón là .
Câu hỏi tương tự:
#7525 THPT Quốc giaToán
Cho hình nón có chiều cao và bán kính đáy đều bằng . Mặt phẳng đi qua đỉnh của hình nón và cắt đường tròn đáy theo một dây cung có độ dài bằng . Khoảng cách từ tâm của đáy tới mặt phẳng bằng
Lượt xem: 128,088 Cập nhật lúc: 22:20 14/05/2025
#8101 THPT Quốc giaToán
Cho hình nón tròn xoay có chiều cao bằng và bán kính đáy bằng . Mặt phẳng đi qua đỉnh của hình nón và cắt hình nón theo thiết diện là một tam giác cân có độ dài cạnh đáy bằng . Diện tích của thiết diện bằng:
Lượt xem: 137,883 Cập nhật lúc: 11:57 16/05/2025
#8749 THPT Quốc giaToán
Cho hình nón có chiều cao
, bán kính đáy . Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là . Tính diện tích của thiết diện đó.Lượt xem: 148,880 Cập nhật lúc: 17:18 17/05/2025
#8326 THPT Quốc giaToán
Cho hình nón tròn xoay có chiều cao bằng , bán kính đáy bằng . Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện bằng . Diện tích của thiết diện đó bằng
Lượt xem: 141,635 Cập nhật lúc: 08:16 13/05/2025
#8372 THPT Quốc giaToán
Cho hình nón đỉnh có chiều cao bằng 6.Trên đường tròn đáy lấy hai điểm sao cho khoảng cách từ tâm đường tròn đáy đến dây bằng 3, biết diện tích tam giác bằng . Tính thể tích khối nón được giới hạn bởi hình nón đã cho.
Lượt xem: 142,475 Cập nhật lúc: 22:42 13/05/2025
#7609 THPT Quốc giaToán
Cho hình nón có thiết diện qua đỉnh là tam giác vuông tại , ( thuộc đường tròn đáy). Biết tam giác có bán kính đường tròn nội tiếp bằng , đường cao tạo với mặt phẳng một góc . Diện tích xung quanh của hình nón đã cho bằng
Lượt xem: 129,512 Cập nhật lúc: 13:13 17/05/2025
#11395 THPT Quốc giaToán
Cho hai mặt phẳng và song song với nhau và cùng cắt khối cầu tâm bán kính thành hai hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách giữa hai mặt phẳng và bằng:
Lượt xem: 193,797 Cập nhật lúc: 08:37 17/05/2025
#8113 THPT Quốc giaToán
Cho khối nón có bán kính đáy bằng , góc ở đỉnh hình nón là . Thể tích khối nón bằng
Lượt xem: 138,014 Cập nhật lúc: 10:44 17/05/2025
#8971 THPT Quốc giaToán
Trong không gian cho mặt cầu . Gọi là mặt phẳng đi qua 2 điểm , và cắt theo giao tuyến là đường tròn sao cho khối nón có đỉnh là tâm của , là hình tròn có thể tích lớn nhất. Biết mặt phẳng có phương trình dạng , khi đó bằng:
Lượt xem: 152,709 Cập nhật lúc: 20:20 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
1,388 xem94 thi
