Cho hai mặt phẳng
và
song song với nhau và cùng cắt khối cầu tâm
bán kính
thành hai hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách
giữa hai mặt phẳng
và
bằng:
A.
B.
C.
D.
Đáp án đúng là: D
Cho hai mặt phẳng và song song với nhau và cùng cắt khối cầu tâm bán kính thành hai hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách giữa hai mặt phẳng và bằng:
Đáp án đúng là: D
Cho hai mặt phẳng
và
song song với nhau và cùng cắt khối cầu tâm
bán kính
thành hai hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách
giữa hai mặt phẳng
và
bằng:
A.
B.
C.
D.
Lời giải
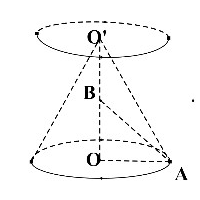
; .
vuông tại nên
vuông tại nên
Diện tích xung quanh của hình nón: .
Đặt .
Xét với .
.
.
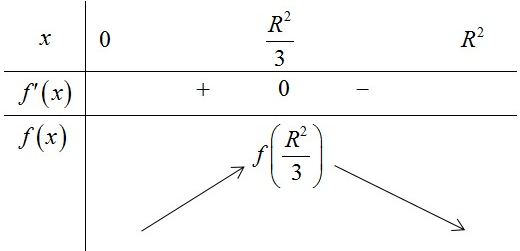
Diện tích xung quanh của hình nón đạt giá trị lớn nhất khi đạt giá trị lớn nhất trên . Khi đó .
Câu hỏi tương tự:
#6132 THPT Quốc giaVật lý
Trong thí nghiệm giao thoa sóng nước, hai nguồn sóng và cách nhau dao động theo phương vuông góc với mặt nước với cùng phương trình tính bằng . Tốc độ truyền sóng bằng và biên độ sóng không đổi trong quá trình truyền đi. Chọn hệ trục thuộc mặt phẳng mặt nước khi yên lặng, gốc O trùng với chứa đoạn . Phía trên mặt nước có một chất điểm chuyển động thẳng đều theo phương ngang với tốc độ sao cho hình chiếu P của nó xuống mặt nước chuyển động với phương trình quỹ đạo . Trong thời gian kể từ lúc P có tọa độ thì P cắt bao nhiêu vân cực đại trong vùng giao thoa sóng?
Lượt xem: 104,350 Cập nhật lúc: 22:47 16/05/2025
#3028 THPT Quốc giaVật lý
Ở mặt nước, hai nguồn sóng kết hợp đặt tại hai điểm và , dao động cùng pha theo phương thẳng đứng, phát ra hai sóng lan truyền có bước sóng . Hai điểm và ở mặt nước sao cho là hình vuông. Trên đoạn thẳng có 19 điểm cực đại giao thoa. Trên đoạn thẳng , gọi là điểm cực đại giao thoa gần nhất và là điểm cực đại giao thoa mà phần tử sóng tại và dao động cùng pha với nhau. Độ dài đoạn thẳng ngắn nhất gần với giá trị nào sau đây?
Lượt xem: 51,559 Cập nhật lúc: 22:40 13/05/2025
#5927 THPT Quốc giaVật lý
Thực hiện giao thoa sóng ở mặt chất lỏng với hai nguồn A và B dao động theo phương thẳng đứng. Hai nguồn cách nhau và dao động với phương trình (t tính bằng . Cho biết tốc độ truyền sóng là . Chỉ xét các vị trí ở mặt chất lỏng nằm trong hình tròn đường kính và thuộc các đường cực đại bậc một. Có bao nhiêu vị trí mà phần tử chất lỏng tại đó dao động cùng pha với các nguồn sóng?
Lượt xem: 100,944 Cập nhật lúc: 08:21 17/05/2025
#871 THPT Quốc giaVật lý
Trên mặt nước có hai nguồn sóng đồng bộ đặt tại hai điểm A và B cách nhau , dao động với phương trình là (u tính bằng cm; t tính bằng ). Tốc độ truyền sóng của mặt nước là . Gọi là điểm ở mặt nước, gần nhất sao cho phần tử nước tại dao động với biên độ cực đại và ngược pha với các nguồn. Khoảng cách từ tới gần nhất với giá trị nào sau đây?
Lượt xem: 14,926 Cập nhật lúc: 21:20 14/05/2025
#5352 THPT Quốc giaVật lý
Ở mặt chất lỏng có hai nguồn sóng cách nhau , dao động theo phương thẳng đứng với phương trình (với tính bằng ). Tốc độ truyền sóng ở mặt chất lỏng là . Gọi là một cực đại trên và gần với trung điểm của nhất, điểm ở mặt chất lỏng nằm trên vân cực đại qua và gần nhất sao cho phần tử chất lỏng tại dao động ngược pha với phần tử tại . Khoảng cách là
Lượt xem: 91,067 Cập nhật lúc: 23:37 12/05/2025
#5418 THPT Quốc giaVật lý
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 18 cm, dao động theo phương thẳng đứng với phương trình (với t tính bằng giây). Tốc độ truyền sóng là 2 m/s. Gọi O là một cực đại trên AB và gần với trung điểm của AB nhất. Điểm M ở mặt chất lỏng nằm trên vân cực đại qua O và gần O nhất sao cho phần tử chất lỏng tại M dao động ngược pha với phần tử tại O. Khoảng cách MO gần nhất với giá trị nào sau đây?
Lượt xem: 92,198 Cập nhật lúc: 18:13 14/05/2025
#8692 THPT Quốc giaToán
Trong không gian , cho hai điểm , . Xét khối nón ngoại tiếp mặt cầu đường kính có là tâm đường tròn đáy khối nón. Gọi là đỉnh của khối nón . Khi thể tích khối nón nhỏ nhất thì mặt phẳng qua đỉnh và song song với mặt phẳng chứa đường tròn đáy của có phương trình . Tính .
Lượt xem: 147,883 Cập nhật lúc: 06:29 15/05/2025
#8566 THPT Quốc giaToán
Cho hình chóp có đáy là hình bình hành. Goi là trung điem cua cạnh . Mặt phȁng đi qua và song song với mặt phȁng chia khối chóp thành hai phần. Tính tỉ số của thể tích phần chứa đỉnh và thể tích phần còn lại.
Lượt xem: 145,714 Cập nhật lúc: 18:37 10/05/2025
#8174 THPT Quốc giaToán
Trong không gian cho mặt phẳng đường thẳng và mặt cầu Gọi là hai điểm trên mặt cầu và là hai điểm nằm trên mặt phẳng sao cho cùng song song với đường thẳng Giá trị lớn nhất của tổng độ dài gần nhất với giá trị nào sau đây
Lượt xem: 139,124 Cập nhật lúc: 00:27 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
324 xem9 thi
