Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7767

Cho hình chóp đều S.ABCDS . A B C D có cạnh đáy bằng 2a2 a, cạnh bên bằng 3a3 a. Khoảng cách từ điểm AA đến mặt phẳng (SCD)\left( S C D \right) bằng

A.  

a143.\dfrac{a \sqrt{14}}{3} .

B.  

a144.\dfrac{a \sqrt{14}}{4} .

C.  

a14.a \sqrt{14} .

D.  

a142.\dfrac{a \sqrt{14}}{2} .

Đáp án đúng là: D



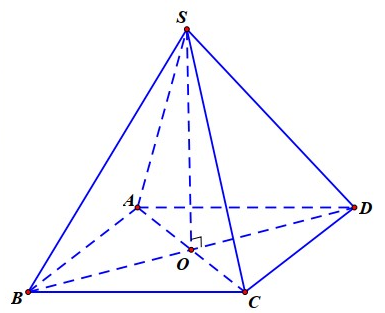
Gọi O=AC∩DBO = A C \cap D B.
Vì S.ABCDS . A B C Dlà hình chóp đều nên SO⊥(ABCD)S O \bot \left( A B C D \right)và đáy ABCDA B C D là hình vuông.
Ta có: d(A,(SCD))d(O,(SCD))=ACOC=2⇒d(A,(SCD))=2d(O,(SCD)).\dfrac{d \left(\right. A , \left( S C D \right) \left.\right)}{d \left(\right. O , \left( S C D \right) \left.\right)} = \dfrac{A C}{O C} = 2 \Rightarrow d \left(\right. A , \left( S C D \right) \left.\right) = 2 d \left(\right. O , \left( S C D \right) \left.\right) .
Tam giác ΔACD\Delta A C D vuông tại DD có: AC=AD2+CD2=2a2⇒OD=OC=a2A C = \sqrt{A D^{2} + C D^{2}} = 2 a \sqrt{2} \Rightarrow O D = O C = a \sqrt{2}.
Tam giác ΔSCO\Delta S C O vuông tại OO có: SO=SC2−OC2=a7S O = \sqrt{S C^{2} - O C^{2}} = a \sqrt{7}.
Do SO,OC,ODS O , O C , O D đôi một vuông góc nên gọi h=d(O,(SCD))h = d \left(\right. O , \left( S C D \right) \left.\right) thì 1h2=1OS2+1OD2+1OC2=87a2⇒h=a144\dfrac{1}{h^{2}} = \dfrac{1}{O S^{2}} + \dfrac{1}{O D^{2}} + \dfrac{1}{O C^{2}} = \dfrac{8}{7 a^{2}} \Rightarrow h = \dfrac{a \sqrt{14}}{4}.
Vậy khoảng cách từ AAđến mặt phẳng (SCD)\left( S C D \right) bằng a142.\dfrac{a \sqrt{14}}{2} .


 

Câu hỏi tương tự:

#8247 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCDS . A B C D có cạnh đáy bằng aa (tham khảo hình vẽ bên). Khoảng cách từ BBđến mặt phẳng (SAC)\left( S A C \right) bằng

Lượt xem: 140,256 Cập nhật lúc: 07:38 22/11/2024

#8391 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa cạnh bên và mặt đáy bằng 60°. Gọi M là trung điểm của SB. Thể tích hình chóp S.ACM bằng

Lượt xem: 142,679 Cập nhật lúc: 06:09 05/11/2024

#8167 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCDS . A B C D có đáy cạnh bằng aa, cạnh bên bằng a52\dfrac{a \sqrt{5}}{2}. Số góc đo giữa hai mặt phẳng (SAB)\left( S A B \right) và (ABCD)\left( A B C D \right) là

Lượt xem: 138,881 Cập nhật lúc: 07:05 22/11/2024

#7903 THPT Quốc giaToán

Cho hình chóp tứ giác đều có cạnh đáy bằng aa và chiều cao bằng a62\dfrac{a \sqrt{6}}{2}. Góc giữa cạnh bên và mặt đáy bằng

Lượt xem: 134,378 Cập nhật lúc: 01:40 08/11/2024

#8011 THPT Quốc giaToán

Cho hình chóp đều S.ABCDS . A B C Dcó đáy ABCDA B C D là hình vuông cạnh bằng

, cạnh bên

.Khoảng cách giữa 2 đường thẳng

và

bằng

Lượt xem: 136,250 Cập nhật lúc: 06:53 22/11/2024

#11178 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình bình hành. Mặt bên SADS A D là tam giác đều cạnh a3a \sqrt{3}. ACDA C D là tam giác vuông tại AA có cạnh AC=aA C = a, góc giữa đường thẳng ABA B và mặt phẳng (SAD)\left( S A D \right) bằng (60)0\left(60\right)^{0}. Thể tích khối chóp S.ABCDS . A B C D bằng

Lượt xem: 190,048 Cập nhật lúc: 08:29 22/11/2024

#8899 THPT Quốc giaToán

Cho hình chóp đều S.ABCDS . A B C D có cạnh đáy bằng aa. Biết khoảng cách giữa hai đường thẳng ACA C và SDS D bằng a3010\dfrac{a \sqrt{30}}{10}. Tính khoảng cách từ điểm BB đến mặt phẳng .

Lượt xem: 151,304 Cập nhật lúc: 15:14 07/11/2024

#11158 THPT Quốc giaToán

Cho hình chóp tam giác đều S.ABCS . A B C có cạnh đáy bằng 2a2 a và chiều cao bằng a2a \sqrt{2} (tham khảo hình vẽ dưới đây)



Khoảng cách từ điểm AA đến mặt phẳng (SBC)\left( S B C \right) bằng

Lượt xem: 189,707 Cập nhật lúc: 19:07 15/11/2024

#8348 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCDS . A B C D có cạnh đáy bằng 2a,2 a , OO là tâm mặt đáy. Khoảng cách giữa hai đường thẳng SOS O và ABA B bằng

Lượt xem: 141,946 Cập nhật lúc: 07:46 22/11/2024


Đề thi chứa câu hỏi này:

67. Đề thi thử TN THPT môn Toán năm 2024 - Sở Bình PhướcTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,357 lượt xem 2,317 lượt làm bài