Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8161

Cho khối chóp tam giác đều

Hình ảnh

biết AB=aA B = a và SA=2aS A = 2 a. Tính chiều cao của khối chóp

Hình ảnh

.

A.  

V=a339V = \dfrac{a \sqrt{33}}{9}

B.  

V=a333V = \dfrac{a \sqrt{33}}{3}

C.  

V=a1416V = \dfrac{a \sqrt{141}}{6}

D.  

V=a63V = \dfrac{a \sqrt{6}}{3}

Đáp án đúng là: B

Cho khối chóp tam giác đều

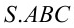
biết AB=aA B = a và SA=2aS A = 2 a. Tính chiều cao của khối chóp

.
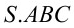
A. V=a339V = \dfrac{a \sqrt{33}}{9}B. V=a333V = \dfrac{a \sqrt{33}}{3}C. V=a1416V = \dfrac{a \sqrt{141}}{6}D. V=a63V = \dfrac{a \sqrt{6}}{3}
Lời giải



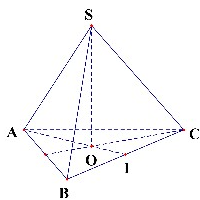
Do đáy là tam giác đều nên gọi

là trung điểm cạnh

, khi đó

là đường cao của tam giác đáy. Chiều cao của chóp là SOS O
Theo định lý Pitago ta có

, và

.
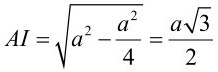
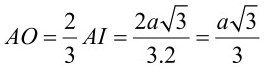
Trong tam giác

vuông tại

ta có SO=4a2−a23=a333S O = \sqrt{4 a^{2} - \dfrac{a^{2}}{3}} = \dfrac{a \sqrt{33}}{3}.


 

Câu hỏi tương tự:

#7561 THPT Quốc giaToán

Cho khối chóp S.ABCS . A B C có đáy ABCA B C là tam giác vuông tại AA, biết AB=a,  AC=2aA B = a , \textrm{ }\textrm{ } A C = 2 a. Mặt bên (SAB)\left( S A B \right) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo aa thể tích khối chóp S.ABCS . A B C.

Lượt xem: 128,651 Cập nhật lúc: 06:18 23/02/2025

#8395 THPT Quốc giaToán

Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABCD theo a.

Lượt xem: 142,811 Cập nhật lúc: 23:06 22/02/2025

#8205 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy ABCA B C là tam giác đều cạnh 3. Các mặt bên (SAB)\left( S A B \right), (SAC)\left( S A C \right), (SBC)\left( S B C \right) lần lượt tạo với đáy các góc là 30∘, 45∘, 60∘30 \circ , \text{ } 45 \circ , \text{ } 60 \circ. Tính thể tích của khối chóp S.ABCS . A B C. Biết rằng hình chiếu vuông góc của SS trên (ABC)\left( A B C \right) nằm trong tam giác ABCA B C.

Lượt xem: 139,594 Cập nhật lúc: 16:44 22/02/2025

#7529 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy là tam giác đều cạnh a,a , cạnh bên SAS A vuông góc với đáy và SA=a3S A = a \sqrt{3}. Tính thể tích khối chóp S.ABC.S . A B C .

Lượt xem: 128,039 Cập nhật lúc: 17:13 23/02/2025

#11178 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình bình hành. Mặt bên SADS A D là tam giác đều cạnh a3a \sqrt{3}. ACDA C D là tam giác vuông tại AA có cạnh AC=aA C = a, góc giữa đường thẳng ABA B và mặt phẳng (SAD)\left( S A D \right) bằng (60)0\left(60\right)^{0}. Thể tích khối chóp S.ABCDS . A B C D bằng

Lượt xem: 190,076 Cập nhật lúc: 13:26 23/02/2025

#8157 THPT Quốc giaToán

Cho một khối chóp tam giác có đáy là tam giác vuông và độ dài hai cạnh góc vuông lần lượt là 4a4 a và 3a, 3 a , \textrm{ }chiều cao của khối chóp là 4a.4 a . Thể tích (tính theo aa) của khối chóp đó là

Lượt xem: 138,722 Cập nhật lúc: 23:05 22/02/2025

#8136 THPT Quốc giaToán

Cho khối chóp S.ABCS . A B C có đáy là tam giác vuông cân tại BB. Khoảng cách từ AA đến mặt phẳng (SBC)\left( S B C \right) bằng a2a \sqrt{2}, SAB^=SCB^=90∘\hat{S A B} = \hat{S C B} = 90 \circ. Khi độ dài cạnh ABA B thay đổi, thể tích khối chóp S.ABCS . A B C có giá trị nhỏ nhất bằng

Lượt xem: 138,363 Cập nhật lúc: 06:39 23/02/2025

#8184 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy ABCA B C là tam giác vuông tại AA, AB=aA B = a, AC=a2A C = a \sqrt{2}. Biết thể tích khối chóp S.ABCS . A B C bằng a32\dfrac{a^{3}}{2}. Khoảng cách từ SS đến mặt phẳng (ABC)\left( A B C \right) bằng

Lượt xem: 139,174 Cập nhật lúc: 23:12 22/02/2025

#8523 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy ABCA B C là tam giác vuông tại BB và cạnh bên SAS A vuông góc với đáy. Gọi MM là trung điểm của SC,S C , biết AB=a,  AC=2a,  SA=a3.A B = a , \textrm{ }\textrm{ } A C = 2 a , \textrm{ }\textrm{ } S A = a \sqrt{3} . Tính thể tích khối chóp S.AMBS . A M B theo a.a .

Lượt xem: 145,006 Cập nhật lúc: 16:58 22/02/2025


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - THPT LIÊN TRƯỜNG NGHỆ AN THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

919 lượt xem 441 lượt làm bài