Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7679

Cho khối lăng trụ đều ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có cạnh đáy bằng 2a2 a. Biết khoảng cách từ điểm A′A^{'} đến mặt phẳng \left(\right. A B^{'} C^{'} \right) bằng aa. Thể tích của khối lăng trụ đã cho là

A.  

32a36\dfrac{3 \sqrt{2} a^{3}}{6}.

B.  

32a38\dfrac{3 \sqrt{2} a^{3}}{8}.

C.  

32a32\dfrac{3 \sqrt{2} a^{3}}{2}.

D.  

2a32\dfrac{\sqrt{2} a^{3}}{2}.

Đáp án đúng là: B

Cho khối lăng trụ đều ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có cạnh đáy bằng 2a2 a. Biết khoảng cách từ điểm A′A^{'} đến mặt phẳng (AB′C′)\left( A B^{'} C^{'} \right) bằng aa. Thể tích của khối lăng trụ đã cho là
A. 32a36\dfrac{3 \sqrt{2} a^{3}}{6}. B. 32a38\dfrac{3 \sqrt{2} a^{3}}{8}. C. 32a32\dfrac{3 \sqrt{2} a^{3}}{2}. D. 2a32\dfrac{\sqrt{2} a^{3}}{2}.
Lời giải



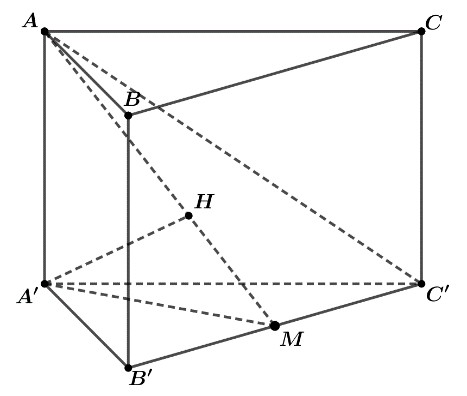
Gọi MM là trung điểm của B′C′B^{'} C^{'}.
Ta có ⇒(AB′C′)⊥(AA′M)\Rightarrow \left( A B^{'} C^{'} \right) \bot \left( A A^{'} M \right).
Trong mặt phẳng (AA′M)\left( A A^{'} M \right), kẻ A′H⊥AMA^{'} H \bot A M, suy ra A′H⊥(AB′C′)A^{'} H \bot \left( A B^{'} C^{'} \right).
Vậy khoảng cách từ A′A^{'} đến mặt phẳng (AB′C′)\left( A B^{'} C^{'} \right) là A′H=aA^{'} H = a. AM=a3A M = a \sqrt{3}
Ta có 1A′H2=1A′A2+1A′M2\dfrac{1}{A^{'} H^{2}} = \dfrac{1}{A^{'} A^{2}} + \dfrac{1}{A^{'} M^{2}} ⇒1A′A2=1A′H2−1A′M2=23a2\Rightarrow \dfrac{1}{A^{'} A^{2}} = \dfrac{1}{A^{'} H^{2}} - \dfrac{1}{A^{'} M^{2}} = \dfrac{2}{3 a^{2}} ⇒A′A=a62\Rightarrow A^{'} A = \dfrac{a \sqrt{6}}{2}.
Vậy thể tích khối lăng trụ là V=AA′.SA′B′C′=a62.a234=3a328V = A A^{'} . S_{A^{'} B^{'} C^{'}} = \dfrac{a \sqrt{6}}{2} . \dfrac{a^{2} \sqrt{3}}{4} = \dfrac{3 a^{3} \sqrt{2}}{8}.


 

Câu hỏi tương tự:

#7977 THPT Quốc giaToán

Cho lăng trụ ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy ABCA B C là tam giác đều cạnh bằng aa, biết A′A=A′B=A′C=aA^{'} A = A^{'} B = A^{'} C = a. Tính thể tích khối lăng trụ ABC.A′B′C′A B C . A^{'} B^{'} C^{'} ?

Lượt xem: 135,651 Cập nhật lúc: 13:22 18/01/2025

#7587 THPT Quốc giaToán

Cho lăng trụ tam giác đều ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có độ dài cạnh đáy và cạnh bên bằng

. Gọi các điểm M , N , EM \textrm{ } , \textrm{ } N \textrm{ } , \textrm{ } E lần lượt là trung điểm các cạnh BC , CC′ , A′C′B C \textrm{ } , \textrm{ } C C^{'} \textrm{ } , \textrm{ } A^{'} C^{'}. Mặt phẳng (MNE)\left( M N E \right) chia khối lăng trụ đã cho thành hai phần có thể tích là thể tích khối đa diện chứa điểm . Tỷ số

bằng

Lượt xem: 129,020 Cập nhật lúc: 10:43 18/01/2025

#7923 THPT Quốc giaToán

Cho hình lăng trụ đều có đáy là tam giác đều cạnh bằng aa, cạnh bên bằng 2a2 a. Tính thể tích khối lăng trụ đó.

Lượt xem: 134,794 Cập nhật lúc: 13:04 18/01/2025

#8579 THPT Quốc giaToán

Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng aa. Thể tích khối lăng trụ đó là

Lượt xem: 145,931 Cập nhật lúc: 13:15 18/01/2025

#8827 THPT Quốc giaToán

Cho hình lăng trụ ABC.A′B′C′A B C . A ' B ' C 'có các mặt bên đều là hình vuông. Gọi M,NM , Nlần lượt là trung điểm của các cạnh BC,​A′C′B C , ​ A ' C '. Biết khoảng cách giữa hai đường thẳng MNM Nvà AB′A B ' bằng a32\dfrac{a \sqrt{3}}{2}. Thể tích khối chóp A′ABCA ' A B C bằng

Lượt xem: 150,139 Cập nhật lúc: 05:45 17/01/2025

#8783 THPT Quốc giaToán

Cho khối lăng trụ đều ABC.A′B′C′A B C . A ' B ' C ' có AB=2aA B = 2 a, AA′=a3A A ' = a \sqrt{3}.Thể tích của khối lăng trụ đã cho bằng

Lượt xem: 149,380 Cập nhật lúc: 12:47 17/01/2025

#7727 THPT Quốc giaToán

Cho lăng trụ đều ABC.A′B′C′A B C . A^{'} B^{'} C^{'}. Biết rằng góc giữa (A′BC)\left( A^{'} B C \right) và (ABC)\left( A B C \right) bằng (30)0\left(30\right)^{0}, tam giác A′BCA^{'} B C có diện tích bằng 8. Thể tích khối lăng trụ ABC.A′B′C′A B C . A^{'} B^{'} C^{'}

Lượt xem: 131,394 Cập nhật lúc: 13:02 18/01/2025

#8479 THPT Quốc giaToán

Cho hình lăng trụ đều ABC.A′B′C′A B C . A^{'} B^{'} C^{'}. Biết khoảng cách từ điểm CC đến mặt phẳng bằng aa, góc giữa hai mặt phẳng (ABC′)\left( A B C^{'} \right) và (BCC′B′)\left( B C C^{'} B^{'} \right) bằng α\alpha với cosα=123cos \alpha = \dfrac{1}{2 \sqrt{3}}. Tính thể tích khối lăng trụ ABC.A′B′C′A B C . A^{'} B^{'} C^{'}.

Lượt xem: 144,227 Cập nhật lúc: 09:05 17/01/2025

#7954 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A ' B ' C ', biết đáy ABCA B C là tam giác đều cạnh aa. Khoảng cách từ tâm OO của tam giác ABCA B Cđến mặt phẳng (A′BC)\left( A ' B C \right) bằng a6\dfrac{a}{6}. Thể tích khối lăng trụ ABC.A′B′C′A B C . A ' B ' C ' bằng

Lượt xem: 135,312 Cập nhật lúc: 13:03 18/01/2025


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN -SGD-ĐẮK-NÔNG (Bản word kèm giải)THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

1,326 lượt xem 658 lượt làm bài