Một hình nón nằm trong một hình trụ sao cho đáy của hình nón trùng với một đáy của hình trụ còn đỉnh của hình nón trùng với tâm của đáy còn lại của hình trụ. Biết tỉ số của diện tích toàn phần của hình trụ và diện tích toàn phần của hình nón là
, tính tỉ số của chiều cao và bán kính đáy của hình trụ.
A.
B.
C.
D.
Đáp án đúng là: D
Một hình nón nằm trong một hình trụ sao cho đáy của hình nón trùng với một đáy của hình trụ còn đỉnh của hình nón trùng với tâm của đáy còn lại của hình trụ. Biết tỉ số của diện tích toàn phần của hình trụ và diện tích toàn phần của hình nón là , tính tỉ số của chiều cao và bán kính đáy của hình trụ.
Đáp án đúng là: D
Một hình nón nằm trong một hình trụ sao cho đáy của hình nón trùng với một đáy của hình trụ còn đỉnh của hình nón trùng với tâm của đáy còn lại của hình trụ. Biết tỉ số của diện tích toàn phần của hình trụ và diện tích toàn phần của hình nón là
, tính tỉ số của chiều cao và bán kính đáy của hình trụ.
A.
B.
C.
D.
Lời giải
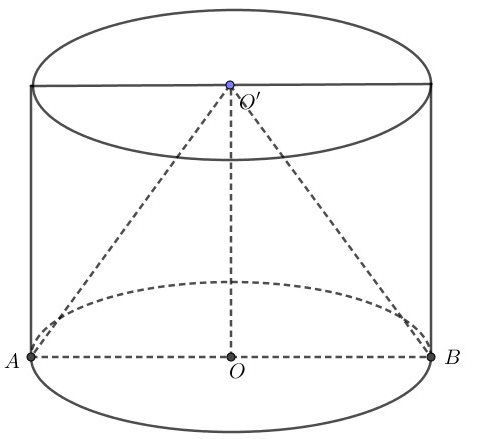
Gọi độ dài bán kính đáy và chiều cao của hình trụ lần lượt là , (với ).
Gọi độ dài đường sinh của hình nón là (với ).
Ta có: .
.
.
Vậy .
Câu hỏi tương tự:
#7652 THPT Quốc giaToán
Một đồ chơi
hình khối nón đặc có bán kính
và chiều cao
. Một hình trụ có bán kính
đang chứa nước có chiều cao mực nước là
. Khi đặt khối nón
lên đáy của hình trụ ( các đáy của chúng cùng nằm trân một mặt phẳng) thì mực nước dâng cao bằng đỉnh của nón. Chiều cao của khối nón là
Lượt xem: 130,160 Cập nhật lúc: 15:56 23/04/2025
#8137 THPT Quốc giaToán
Một hình nón có thiết diện qua trục là một tam giác vuông cân với cạnh góc vuông bằng . Thể tích của khối nón bằng
Lượt xem: 138,475 Cập nhật lúc: 07:26 26/04/2025
#8612 THPT Quốc giaToán
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng . Tính diện tích xung quanh của hình nón.
Lượt xem: 146,540 Cập nhật lúc: 02:37 23/04/2025
#8392 THPT Quốc giaToán
Cắt hình nón bằng một mặt phẳng qua đỉnh S và tạo với trục của hình nón một góc bằng ta được thiết diện là tam giác SAB vuông và có diện tích bằng . Chiều cao của hình nón bằng
Lượt xem: 142,815 Cập nhật lúc: 07:20 26/04/2025
#7914 THPT Quốc giaToán
Cắt hình nón đỉnh bởi một mặt phẳng đi qua trục hình nón ta được một tam giác vuông cân có cạnh huyền bằng là dây cung của đường tròn đáy hình nón sao cho mặt phẳng tạo với mặt phẳng chứa đáy hình nón một góc . Diện tích của tam giác bằng
Lượt xem: 134,617 Cập nhật lúc: 16:31 24/04/2025
#11395 THPT Quốc giaToán
Cho hai mặt phẳng và song song với nhau và cùng cắt khối cầu tâm bán kính thành hai hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách giữa hai mặt phẳng và bằng:
Lượt xem: 193,786 Cập nhật lúc: 08:02 26/04/2025
#8360 THPT Quốc giaToán
Cho hình nón có bán kính đáy bằng 3 chiều cao bằng 6, một khối trụ có bán kính đáy thay đổi nội tiếp khối nón đã cho (như hình vẽ). Khi thể tích khối trụ đạt giá trị lớn nhất thì diện tích toàn phần của hình trụ bằng
Lượt xem: 142,205 Cập nhật lúc: 06:28 22/04/2025
#8749 THPT Quốc giaToán
Cho hình nón có chiều cao
, bán kính đáy . Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là . Tính diện tích của thiết diện đó.Lượt xem: 148,868 Cập nhật lúc: 19:52 25/04/2025
#8843 THPT Quốc giaToán
Cho hình nón có bán kính đáy bằng 4, chiều cao bằng 8. Một khối trụ có bán kính đáy thay đổi và nội tiếp hình nón đã cho (tham khảo hình vẽ). Thể tích của khối trụ đạt giá trị lớn nhất bằng
Lượt xem: 150,486 Cập nhật lúc: 10:29 26/04/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
543 xem33 thi
