Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8134

Tìm tất cả các giá trị thực của mm để phương trình ∣x4−2x2−3∣=2m−1\left|\right. x^{4} - 2 x^{2} - 3 \left|\right. = 2 m - 1 có đúng 6 nghiệm thực phân biệt

A.  

3<m<43 < m < 4

B.  

2<m<522 < m < \dfrac{5}{2}

C.  

1<m<321 < m < \dfrac{3}{2}.

D.  

4<m<54 < m < 5.

Đáp án đúng là: B

Tìm tất cả các giá trị thực của mm để phương trình ∣x4−2x2−3∣=2m−1\left|\right. x^{4} - 2 x^{2} - 3 \left|\right. = 2 m - 1 có đúng 6 nghiệm thực phân biệt
A. 3<m<43 < m < 4B. 2<m<522 < m < \dfrac{5}{2}C. 1<m<321 < m < \dfrac{3}{2}. D. 4<m<54 < m < 5.
Lời giải
Xét hàm số f(x)=x4−2x2−3f \left( x \right) = x^{4} - 2 x^{2} - 3
f′(x)=4x3−4xf^{'} \left( x \right) = 4 x^{3} - 4 x
f′(x)=0⇔[x=0x=±1f^{'} \left( x \right) = 0 \Leftrightarrow \left[\right. x = 0 \\ x = \pm 1



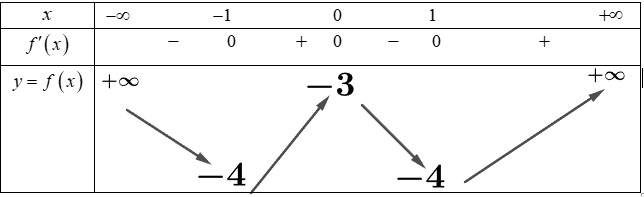
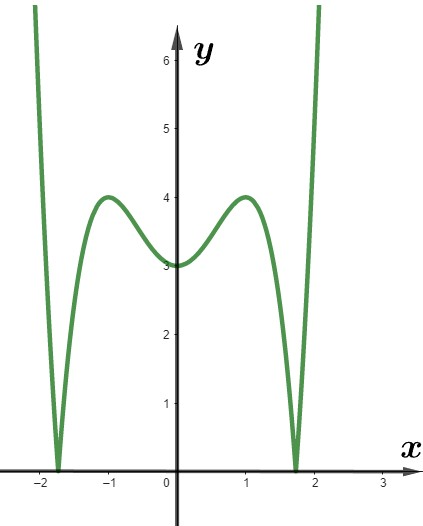
Từ đó ta có đồ thị hàm số y=∣x4−2x2−3∣y = \left|\right. x^{4} - 2 x^{2} - 3 \left|\right.



Để phương trình có 6 nghiệm phân biệt thì 3<2m−1<4⇔2<m<523 < 2 m - 1 < 4 \Leftrightarrow 2 < m < \dfrac{5}{2}.


 

Câu hỏi tương tự:

#8513 THPT Quốc giaToán

Cho hàm số y=−x4+2x2y = - x^{4} + 2 x^{2} có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số mm để phương trình −x4+2x2=m- x^{4} + 2 x^{2} = m có bốn nghiệm thực phân biệt.


Lượt xem: 144,792 Cập nhật lúc: 14:09 23/11/2024

#8613 THPT Quốc giaToán

Tìm tất cả các giá trị thực của tham số mm để bất phương trình (log)2(5x−1).(log)2(2.5x−2)≤m\left(log\right)_{2} \left( 5^{x} - 1 \right) . \left(log\right)_{2} \left( 2 . 5^{x} - 2 \right) \leq m có nghiệm x≥1x \geq 1?

Lượt xem: 146,487 Cập nhật lúc: 04:02 24/11/2024

#7922 THPT Quốc giaToán

Tìm tất cả các giá trị thực của tham số mm để hàm số y=mx+(m+1)x−2y = m x + \left( m + 1 \right) \sqrt{x - 2} nghịch biến trên (2;+∞)\left( 2 ; + \infty \right).

Lượt xem: 134,741 Cập nhật lúc: 13:00 23/11/2024

#7564 THPT Quốc giaToán

Cho hàm số y=(m+1)x4−mx2+3.y = \left( m + 1 \right) x^{4} - m x^{2} + 3 . Tìm tất cả các giá trị thực của tham số mm để hàm số có ba điểm cực trị

Lượt xem: 128,616 Cập nhật lúc: 07:58 23/11/2024

#8835 THPT Quốc giaToán

Tìm tất cả các giá trị thực của tham số mm sao cho đồ thị hàm số y=2x2−3x+mx−my = \dfrac{2 x^{2} - 3 x + m}{x - m} không có tiệm cận đứng.

Lượt xem: 150,259 Cập nhật lúc: 04:19 23/11/2024

#8535 THPT Quốc giaToán

Xét hàm số f(t)=9t9t+m2f \left( t \right) = \dfrac{9^{t}}{9^{t} + m^{2}} với mm là tham số thực. Gọi SS là tập hợp tất cả các giá trị của mm sao cho Tìm tổng các phần tử của tập SS.

Lượt xem: 145,163 Cập nhật lúc: 04:24 23/11/2024

#8506 THPT Quốc giaToán

Tìm tất cả các giá trị của tham số mm để đồ thị hàm số y=mx4+(m−1)x2+2022y = m x^{4} + \left( m - 1 \right) x^{2} + 2022 có đúng một điểm cực đại.

Lượt xem: 144,668 Cập nhật lúc: 18:49 22/11/2024

#8597 THPT Quốc giaToán

Tìm tất cả các giá trị mm để phương trình x3−3x−m+1=0x^{3} - 3 x - m + 1 = 0 có 3 nghiệm phân biệt.

Lượt xem: 146,216 Cập nhật lúc: 10:23 23/11/2024

#7929 THPT Quốc giaToán

Tìm tất cả các giá trị của tham số mm để đồ thị hàm số y=x3−2mx2+(2m2−1)x+m(1−m2)y = x^{3} - 2 m x^{2} + \left( 2 m^{2} - 1 \right) x + m \left( 1 - m^{2} \right) cắt trục hoành tại 3 điểm phân biệt có hoành độ dương.

Lượt xem: 134,851 Cập nhật lúc: 02:29 24/11/2024


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - THPT HUYỆN NAM TRỰC NAM ĐỊNH - Lần 1THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

749 lượt xem 371 lượt làm bài