Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8522

Tính thể tích của khối tứ diện đều biết chiều cao tứ diện bằng aa.

A.  

38a3\dfrac{\sqrt{3}}{8} a^{3}.

B.  

33a3\dfrac{\sqrt{3}}{3} a^{3}

C.  

62a3\dfrac{\sqrt{6}}{2} a^{3}.

D.  

63a3\dfrac{\sqrt{6}}{3} a^{3}.

Đáp án đúng là: A

Tính thể tích của khối tứ diện đều biết chiều cao tứ diện bằng aa.
A. 38a3\dfrac{\sqrt{3}}{8} a^{3}. B. 33a3\dfrac{\sqrt{3}}{3} a^{3}C. 62a3\dfrac{\sqrt{6}}{2} a^{3}. D. 63a3\dfrac{\sqrt{6}}{3} a^{3}.
Lời giải



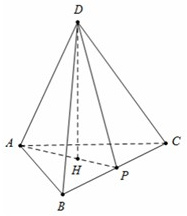
Xét tứ diện đều ABCDA B C Dcạnh AB=xA B = x, PPlà trung điểm BCB C, đường cao DH=aD H = a
AP=x32⇒AH=x33A P = \dfrac{x \sqrt{3}}{2} \Rightarrow A H = \dfrac{x \sqrt{3}}{3}. Áp dụng định lí Pi-ta-go trong tam giác ADHA D Hta có: DH2+HA2=DA2⇒a2+x23=x2⇒x=a62D H^{2} + H A^{2} = D A^{2} \Rightarrow a^{2} + \dfrac{x^{2}}{3} = x^{2} \Rightarrow x = \dfrac{a \sqrt{6}}{2}.
Do đó: SΔABC=x234=3a238S_{\Delta A B C} = \dfrac{x^{2} \sqrt{3}}{4} = \dfrac{3 a^{2} \sqrt{3}}{8}
Vậy VABCD=13.DH.SΔABC=a338V_{A B C D} = \dfrac{1}{3} . D H . S_{\Delta A B C} = \dfrac{a^{3} \sqrt{3}}{8}.


 

Câu hỏi tương tự:

#7898 THPT Quốc giaToán

Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB=6a,AC=9a,AD=3aA B = 6 a , A C = 9 a , A D = 3 a. Gọi M, N, P lần lượt là trọng tâm của các tam giác ABC, ACD, ADB. Tính thể tích V của khối tứ diện AMNP.

Lượt xem: 134,302 Cập nhật lúc: 13:06 18/01/2025

#8810 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCDS . A B C D có góc giữa mặt phẳng chứa mặt bên và mặt phẳng đáy bằng 60∘60 \circ. Biết rằng mặt cầu ngoại tiếp hình chóp S.ABCDS . A B C D có bán kính R=3.R = \sqrt{3} . Tính thể tích của khối chóp S.ABCS . A B C.

Lượt xem: 149,808 Cập nhật lúc: 23:17 18/01/2025

#7988 THPT Quốc giaToán

Để chế tạo một chi tiết máy, từ một khối thép hình trụ có đường kính 10cm10 c m và chiều cao 30cm,30 c m , người ta tiện bỏ xung quanh hai đầu rộng 1cm1 c m và sâu 1cm1 c m (tham khảo hình vẽ). Tinh thể tích của chi tiết máy đó, làm tròn kết quả đến hàng phần trăm?

Lượt xem: 135,832 Cập nhật lúc: 23:19 18/01/2025

#8311 THPT Quốc giaToán

Một khúc gỗ có dạng hình khối nón có bán kính đáy r=2mr = 2 m, chiều cao h=6mh = 6 m. Bác thợ mộc chế tác từ gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ. Gọi VVlà thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính VV.

Lượt xem: 141,395 Cập nhật lúc: 00:24 19/01/2025

#7672 THPT Quốc giaToán

Tính thể tích của khối lập phương ABCDA′B′C′D′A B C D A ' B ' C ' D ', biết AC′=a3A C ' = a \sqrt{3}.

Lượt xem: 130,454 Cập nhật lúc: 12:26 19/01/2025

#8492 THPT Quốc giaToán

Cho hình chóp có diện tích đáy bằng 6a26 a^{2} và chiều cao bằng 10a10 a. Tính thể tích VV của khối chóp đã cho.

Lượt xem: 144,409 Cập nhật lúc: 09:15 19/01/2025

#8079 THPT Quốc giaToán

Một khối nón có bán kính đường tròn đáy r=3r = 3 và độ dài đường sinh l=5l = 5. Tính thể tích của khối nón đó.

Lượt xem: 137,378 Cập nhật lúc: 19:35 18/01/2025

#11404 THPT Quốc giaToán

Cho khối lăng trụ ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy ABCA B C là tam giác vuông cân tại BB và AC=2aA C = 2 a. Hình chiếu vuông góc của A′A^{'} trên mặt phẳng (ABC)\left( A B C \right) là trung điểm HH của cạnh ABA B và AA′=a2A A^{'} = a \sqrt{2}. Tính thể tích VV của khối lăng trụ đã cho.

Lượt xem: 193,927 Cập nhật lúc: 10:54 18/01/2025

#7565 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy là tam giác ABCA B C vuông cân tại AA, cạnh BC=a2B C = a \sqrt{2}. Góc giữa mặt phẳng (AB′C)\left( A B^{'} C \right) và mặt phẳng (BCC′B′)\left( B C C^{'} B^{'} \right) bằng 60∘60 \circ. Tính thể tích VV của khối đa diện AB′CA′C′A B^{'} C A^{'} C^{'}.

Lượt xem: 128,708 Cập nhật lúc: 12:01 19/01/2025


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - Chuyên Hạ Long - Quảng Ninh - Lần 1 THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

334 lượt xem 126 lượt làm bài