Trên mặt nước có hai nguồn kết hợp được đặt ở
và
cách nhau
, dao động điều hòa cùng tần số, cùng pha, theo phương vuông góc với mặt nước. sóng truyền trên mặt nước với bước sóng
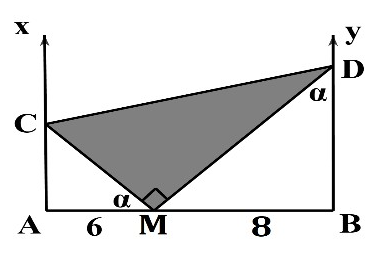
. Điểm
nằm trên đoạn
cách
một đoạn
. Gọi
, By là hai nửa đường thẳng trên mặt nước ở cùng một phía so với
và vuông góc với
. Cho điểm
di chuyển trên
và điểm
di chuyển trên By sao cho
luôn vuông góc với
Khi tổng diện tích của tam giác
và
có giá trị nhỏ nhất thì số điểm dao động với biên độ cực đại trên MD là
A. 19
B. 12
C. 13
D. 20
Đáp án đúng là: C
Trên mặt nước có hai nguồn kết hợp được đặt ở và cách nhau , dao động điều hòa cùng tần số, cùng pha, theo phương vuông góc với mặt nước. sóng truyền trên mặt nước với bước sóng . Điểm nằm trên đoạn cách một đoạn . Gọi , By là hai nửa đường thẳng trên mặt nước ở cùng một phía so với và vuông góc với . Cho điểm di chuyển trên và điểm di chuyển trên By sao cho luôn vuông góc với Khi tổng diện tích của tam giác và có giá trị nhỏ nhất thì số điểm dao động với biên độ cực đại trên MD là
19
12
13
20
Đáp án đúng là: C
Đặt
(cùng phụ
)
Dấu = xảy ra khi
Trên MD có
có 13 giá trị k nguyên. Chọn C
Câu hỏi tương tự:
#190 THPT Quốc giaVật lý
Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp được đặt tại A và dao động theo phương trình ( không đổi, tính bằng ). Tốc độ truyền sóng trong nước là . Hai điểm nằm trên mặt nước có hiệu khoảng cách đến hai nguồn là . Kết luận về dao động của là
Lượt xem: 3,338 Cập nhật lúc: 12:53 17/05/2025
#1188 THPT Quốc giaVật lý
Trên mặt nước, hai nguồn kết hợp được đặt ở và cách nhau , dao động điều hòa cùng pha, đều theo phương vuông góc với mặt nước. Sóng truyền trên mặt nước với bước sóng 0,8 . Điểm nằm trên đoạn , cách một đoạn . , By là hai nửa đường thẳng trên mặt nước, ở cùng một phía so với và vuông góc với AB. Cho điểm di chuyển trên và điểm di chuyển trên sao cho luôn vuông góc với MD. Khi diện tích của có giá trị nhỏ nhất thì số điểm dao động với biên độ cực đại trên là
Lượt xem: 20,304 Cập nhật lúc: 17:48 17/05/2025
#2689 THPT Quốc giaVật lý
Tại mặt nước, hai nguồn kết hợp được đặt tại hai điểm và cách nhau , dao động điều hòa, cùng tần số, cùng pha theo phương vuông góc với mặt nước. Trên , hai phần tử nước dao động với biên độ cực đại có vị trí cân bằng cách nhau một đoạn ngắn nhất là . Điểm là vị trí cân bằng của phần tử ở mặt nước sao cho Phần tử nước ở dao động với biên độ cực đại. Khoảng cách lớn nhất bằng:
Lượt xem: 45,825 Cập nhật lúc: 12:12 17/05/2025
#6734 THPT Quốc giaVật lý
Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn kết hợp đặt tại hai điểm và dao động cùng pha theo phương thẳng đứng. Trên đoạn thẳng , người ta đo được khoảng cách giữa 10 cực đại giao thoa liên tiếp là . Bước sóng có giá trị là:
Lượt xem: 114,579 Cập nhật lúc: 16:12 14/05/2025
#4828 THPT Quốc giaVật lý
Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm A và B, dao động cùng pha theo phương thẳng đứng. Trên đoạn thẳng AB quan sát được 15 điểm cực đại giao thoa. Ở mặt nước, đường tròn (C) có tâm O thuộc đường trung trực của AB và bán kính a không đổi (với 2a < AB). Khi dịch chuyển (C) trên mặt nước sao cho tâm O luôn nằm trên đường trung trực của AB thì thấy trên (C) có tối đa 12 điểm cực đại giao thoa. Khi trên (C) có 12 điểm cực đại giao thoa thì trong số đó có 4 điểm mà phần tử tại đó dao động cùng pha với hai nguồn. Độ dài đoạn thẳng AB gần nhất với giá trị nào sau đây?
Lượt xem: 82,162 Cập nhật lúc: 16:00 17/05/2025
#1230 THPT Quốc giaVật lý
Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn kết hợp đặt tại hai điểm và dao động cùng pha theo phương thẳng đứng. Trên đoạn thẳng quan sát được 12 điểm cực tiểu giao thoa. Gọi là đường thẳng thuộc mặt nước đi qua và vuông góc với ; Trên có 6 điểm cực đại giao thoa và ngược pha với nguồn. Số điểm cực đại giao thoa và cùng pha với nguồn trên là
Lượt xem: 20,996 Cập nhật lúc: 22:19 13/05/2025
#11638 THPT Quốc giaVật lý
Giao thoa ở mặt nước được tạo bởi hai nguồn sóng kết hợp dao động điều hòa cùng pha theo phương thẳng đứng tại hai vị trí S1 và S2. Sóng truyền trên mặt nước có bước sóng 12 cm. Trên đoạn thẳng S1S2, hai điểm gần nhau nhất mà phần tử nước tại đó dao động với biên độ cực đại cách nhau
Lượt xem: 197,985 Cập nhật lúc: 06:31 15/05/2025
#7016 THPT Quốc giaVật lý
Trên mặt nước có hai nguồn kết hợp tại và cách nhau lần lượt dao động theo phương trình . Xét về một phía của đường trung trực của , người ta thấy điểm có nằm trên vân giao thoa cực tiểu thứ kể từ đường trung trực của và điểm có nằm trên vân giao thoa cực tiểu thứ . Số điểm dao động với biên độ cực đại trên đoạn bằng
Lượt xem: 119,420 Cập nhật lúc: 08:35 17/05/2025
#3195 THPT Quốc giaVật lý
Trên mật nước có hai nguồn kết hợp và dao động cùng phương thẳng đứng, cùng tần số, cùng pha cách nhau một khoảng . Điểm P xa nhất thuộc mặt nước trên đường thẳng vuông góc với tại dao động với biên độ cực đại. Nếu thì số cực tiểu trên khoảng O1P là
Lượt xem: 54,475 Cập nhật lúc: 18:00 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 40 câu hỏi 40 phút
5,900 xem436 thi
