Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8174

Trong không gian Oxyz,O x y z , cho mặt phẳng (P):x−y+z+7=0,\left( P \right) : x - y + z + 7 = 0 , đường thẳng d:x1=y−2=z2d : \dfrac{x}{1} = \dfrac{y}{- 2} = \dfrac{z}{2} và mặt cầu (S):((x−1))2+y2+((z−2))2=5.\left( S \right) : \left(\left( x - 1 \right)\right)^{2} + y^{2} + \left(\left( z - 2 \right)\right)^{2} = 5 . Gọi A,  BA , \textrm{ }\textrm{ } B là hai điểm trên mặt cầu (S)\left( S \right) và AB=4;A B = 4 ; A′,  B′A^{'} , \textrm{ }\textrm{ } B^{'} là hai điểm nằm trên mặt phẳng (P)\left( P \right) sao cho AA′,  BB′A A^{'} , \textrm{ }\textrm{ } B B^{'} cùng song song với đường thẳng d.d . Giá trị lớn nhất của tổng độ dài AA′+ BB′A A^{'} + \textrm{ } B B^{'} gần nhất với giá trị nào sau đây

A.  

13.13 .

B.  

11.11 .

C.  

12.12 .

D.  

14.14 .

Đáp án đúng là: D

Trong không gian Oxyz,O x y z , cho mặt phẳng (P):x−y+z+7=0,\left( P \right) : x - y + z + 7 = 0 , đường thẳng d:x1=y−2=z2d : \dfrac{x}{1} = \dfrac{y}{- 2} = \dfrac{z}{2} và mặt cầu (S):((x−1))2+y2+((z−2))2=5.\left( S \right) : \left(\left( x - 1 \right)\right)^{2} + y^{2} + \left(\left( z - 2 \right)\right)^{2} = 5 . Gọi A,  BA , \textrm{ }\textrm{ } B là hai điểm trên mặt cầu (S)\left( S \right) và AB=4;A B = 4 ; A′,  B′A^{'} , \textrm{ }\textrm{ } B^{'} là hai điểm nằm trên mặt phẳng (P)\left( P \right) sao cho AA′,  BB′A A^{'} , \textrm{ }\textrm{ } B B^{'} cùng song song với đường thẳng d.d . Giá trị lớn nhất của tổng AA′+ BB′A A^{'} + \textrm{ } B B^{'} gần nhất với giá trị nào sau đây
A. 13.13 .B. 11.11 .C. 12.12 .D. 14.14 .
Lời giải



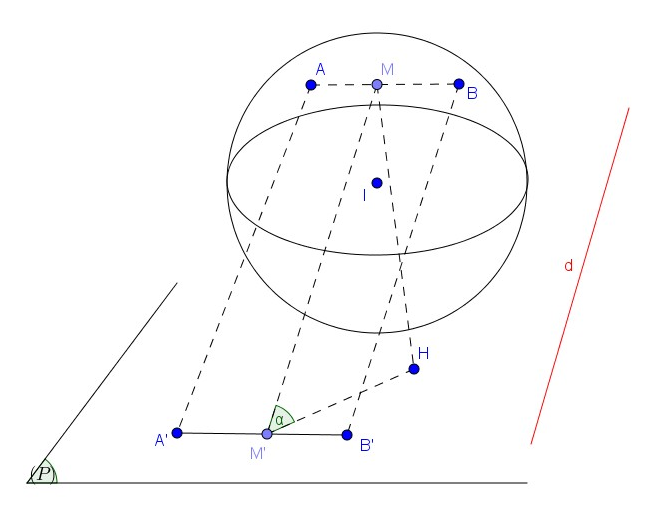
Mặt cầu (S)\left( S \right) có tâm I(1;0;2)I \left( 1 ; 0 ; 2 \right) và bán kính R=5R = \sqrt{5}.
d(I;(P))=1033>Rd \left(\right. I ; \left( P \right) \left.\right) = \dfrac{10 \sqrt{3}}{3} > R nên (P)\left( P \right) và mặt cầu (S)\left( S \right) không giao nhau.
Gọi MM là trung điểm của ABA B, M′M^{'} là trung điểm của A′B′A ' B ' thì AA′+BB′=2MM′=2.MHsin(M;(P))A A ' + B B ' = 2 M M^{'} = 2 . \dfrac{M H}{sin \left(\right. M ; \left( P \right) \left.\right)}.
Khi đó MHmax=R2−AB24+d(I;(P))=5−4+1033=3+1033M H_{max} = \sqrt{R^{2} - \dfrac{A B^{2}}{4}} + d \left(\right. I ; \left( P \right) \left.\right) = \sqrt{5 - 4} + \dfrac{10 \sqrt{3}}{3} = \dfrac{3 + 10 \sqrt{3}}{3}.
Ta có sin(M;(P))=sin(d;(P))=539sin \left(\right. M ; \left( P \right) \left.\right) = sin \left(\right. d ; \left( P \right) \left.\right) = \dfrac{5 \sqrt{3}}{9}.
Vậy ((AA′+ BB′))max=2.3+1033539=60+635≈14,08\left(\left( A A^{'} + \textrm{ } B B^{'} \right)\right)_{max} = 2 . \dfrac{\dfrac{3 + 10 \sqrt{3}}{3}}{\dfrac{5 \sqrt{3}}{9}} = \dfrac{60 + 6 \sqrt{3}}{5} \approx 14 , 08.


 

Câu hỏi tương tự:

#7763 THPT Quốc giaToán

Trong không gian với hệ tọa độ OxyzO x y z, cho đường thẳng (d): x1=y+22=z−1\left( d \right) : \textrm{ } \dfrac{x}{1} = \dfrac{y + 2}{2} = \dfrac{z}{- 1} và mặt phẳng (P):  2x+y+z−1=0\left( P \right) : \textrm{ }\textrm{ } 2 x + y + z - 1 = 0. Phương trình đường thẳng Δ\Delta nằm trong (P)\left( P \right), cắt (d)\left( d \right) và tạo với (d)\left( d \right) một góc 30∘30 \circ đi qua điểm nào sau đây:

Lượt xem: 132,070 Cập nhật lúc: 23:45 16/01/2025

#7662 THPT Quốc giaToán

Trong không gian với hệ tọa độ OxyzO x y z, cho đường thẳng Δ:x−21=y+22=z−2\Delta : \dfrac{x - 2}{1} = \dfrac{y + 2}{2} = \dfrac{z}{- 2} và mặt phẳng (P):2x−y+2z−2022=0\left( P \right) : 2 x - y + 2 z - 2022 = 0. Gọi α\alpha là góc giữa đường thẳng Δ\Delta và mặt phẳng (P)\left( P \right). Khẳng định nào sau đây đúng?

Lượt xem: 130,304 Cập nhật lúc: 10:56 18/01/2025

#7780 THPT Quốc giaToán

Trong không gian OxyzO x y z, cho điểm A(1;2;−1)A \left( 1 ; 2 ; - 1 \right), đường thẳng x−31=y−33=z2\dfrac{x - 3}{1} = \dfrac{y - 3}{3} = \dfrac{z}{2} và mặt phẳng (P):x+y−z+3=0\left( P \right) : x + y - z + 3 = 0. Đường thẳng Δ\Delta đi qua AA, cắt dd và song song với (P)\left( P \right) có phương trình là

Lượt xem: 132,339 Cập nhật lúc: 10:06 18/01/2025

#8194 THPT Quốc giaToán

Trong không gian OxyzO x y z, cho điểm A(−2; −2; −7)A \left( - 2 ; \textrm{ } - 2 ; \textrm{ } - 7 \right), đường thẳng d:x−12=y−23=z−34d : \dfrac{x - 1}{2} = \dfrac{y - 2}{3} = \dfrac{z - 3}{4} và mặt cầu (S):((x+3))2+((y+4))2+((z+5))2=729\left( S \right) : \left(\left( x + 3 \right)\right)^{2} + \left(\left( y + 4 \right)\right)^{2} + \left(\left( z + 5 \right)\right)^{2} = 729. Biết điểm BB thuộc giao tuyến của mặt cầu (S)\left( S \right) và mặt phẳng (P):2x+3y+4z−107=0\left( P \right) : 2 x + 3 y + 4 z - 107 = 0. Khi điểm MM di động trên đường thẳng dd thì giá trị nhỏ nhất của biểu thức MA+MBM A + M B bằng

Lượt xem: 139,388 Cập nhật lúc: 16:20 17/01/2025

#7750 THPT Quốc giaToán

Trong không gian với hệ trục tọa độ OxyzO x y z, cho đường thẳng dd và mặt phẳng lần lượt có phương trình x+12=y1=z−21\dfrac{x + 1}{2} = \dfrac{y}{1} = \dfrac{z - 2}{1} và x+y−2z+8=0x + y - 2 z + 8 = 0, điểm A(2;−1;3)A \left( 2 ; - 1 ; 3 \right). Đường thẳng Δ\Delta cắt dd và (P)\left( P \right) lần lượt tại MM và NN sao cho AA là trung điểm của đoạn thẳng MNM N đi qua điểm B(2;m;n)B \left( 2 ; m ; n \right). Tổng m+2nm + 2 n bằng

Lượt xem: 131,794 Cập nhật lúc: 17:20 17/01/2025

#7963 THPT Quốc giaToán

Trong không gian với hệ trục tọa độ OxyzO x y z, cho đường thẳng d: x+22=y+1−3=z1d : \textrm{ } \dfrac{x + 2}{2} = \dfrac{y + 1}{- 3} = \dfrac{z}{1} và mặt cầu (S):(x−2)2+(y+1)2+(z+1)2=6\left( S \right) : \left( x - 2 \right)^{2} + \left( y + 1 \right)^{2} + \left( z + 1 \right)^{2} = 6. Hai mặt phẳng (P),  (Q)\left( P \right) , \textrm{ }\textrm{ } \left( Q \right) chứa dd và cùng tiếp xúc với (S)\left( S \right) lần lượt tại A, BA , \textrm{ } B. Gọi II tà tâm mặt cầu (S)\left( S \right). Giá trị cosAIB^cos \widehat{A I B} bằng

Lượt xem: 135,466 Cập nhật lúc: 13:07 18/01/2025

#8736 THPT Quốc giaToán

Trong không gian với hệ toạ độ OxyzO x y z, cho điểm M(2;−3;1)M \left( 2 ; - 3 ; 1 \right) và mặt phẳng (α):x+3y−z+2=0\left( \alpha \right) : x + 3 y - z + 2 = 0. Đường thẳng dd đi qua điểm MM và vuông góc với mặt phẳng (α)\left( \alpha \right) có phương trình tham số là:

Lượt xem: 148,653 Cập nhật lúc: 12:57 18/01/2025

#7666 THPT Quốc giaToán

Trong không gian OxyzO x y z, cho hai đường thẳng d :  x−13=y+21=z1d \textrm{ } : \textrm{ }\textrm{ } \dfrac{x - 1}{3} = \dfrac{y + 2}{1} = \dfrac{z}{1}; . Gọi Δ\Delta là đường thẳng đi qua , vuông góc với dd và cắt d′d^{'}. Khi đó tọa độ giao điểm của Δ\Delta và mặt phẳng OyzO y z là

Lượt xem: 130,358 Cập nhật lúc: 17:27 17/01/2025

#8472 THPT Quốc giaToán

Trong không gian OxyzO x y z, cho điểm E(2;1;3)E \left( 2 ; 1 ; 3 \right), mặt phẳng (P):2x+2y−z−3=0\left( P \right) : 2 x + 2 y - z - 3 = 0 và mặt cầu (S):(x−3)2+(y−2)2+(z−5)2=36\left( S \right) : \left( x - 3 \right)^{2} + \left( y - 2 \right)^{2} + \left( z - 5 \right)^{2} = 36. Gọi Δ\Delta là đường thẳng đi qua EE, nằm trong (P)\left( P \right) và cắt (S)\left( S \right) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của Δ\Delta là

Lượt xem: 144,065 Cập nhật lúc: 01:13 17/01/2025


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - THPT GIA ĐỊNH - TPHCM THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

1,056 lượt xem 483 lượt làm bài