Trong không gian với hệ trục tọa độ
, cho đường thẳng
và mặt cầu
. Hai mặt phẳng
chứa
và cùng tiếp xúc với
lần lượt tại
. Gọi
tà tâm mặt cầu
. Giá trị
bằng
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: A
Trong không gian với hệ trục tọa độ , cho đường thẳng và mặt cầu . Hai mặt phẳng chứa và cùng tiếp xúc với lần lượt tại . Gọi tà tâm mặt cầu . Giá trị bằng
.
.
.
.
Đáp án đúng là: A
Chọn A
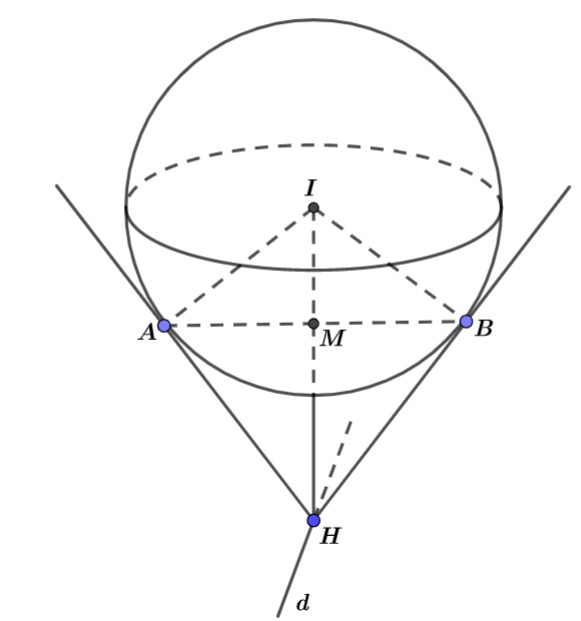
Mặt cầu có tâm và bán kính .
Phương trình tham số của đường thẳng .
Gọi là hình chiếu của lên
Vì .
Khi đó, và
Gọi là hình chiếu của lên .
Xét tam giác vuông tại có:
Xét tam giác vuông tại có .
Tam giác có .
Áp dụng định lý côsin trong tam giác ta có: .
Câu hỏi tương tự:
#7750 THPT Quốc giaToán
Trong không gian với hệ trục tọa độ , cho đường thẳng và mặt phẳng lần lượt có phương trình và , điểm . Đường thẳng cắt và lần lượt tại và sao cho là trung điểm của đoạn thẳng đi qua điểm . Tổng bằng
Lượt xem: 131,841 Cập nhật lúc: 10:40 17/05/2025
#8603 THPT Quốc giaToán
Trong không gian với hệ trục tọa độ , cho ; ; . Diện tích mặt cầu nhận đường tròn ngoại tiếp tam giác làm đường tròn lớn là
Lượt xem: 146,356 Cập nhật lúc: 13:54 17/05/2025
#7583 THPT Quốc giaToán
Trong không gian với hệ trục toạ độ , cho mặt cầu và điểm . Đường thẳng thay đổi, đi qua điểm và cắt mặt cầu tại hai điểm phân biệt. Tính diện tích lớn nhất của tam giác .
Lượt xem: 129,020 Cập nhật lúc: 07:35 17/05/2025
#7605 THPT Quốc giaToán
Trong không gian với hệ trục tọa độ , cho mặt cầu và điểm , biết rằng các tiếp điểm của các tiếp tuyến kẻ từ tới mặt cầu đã cho luôn thuộc một đường tròn có tâm . Giá trị bằng
Lượt xem: 129,419 Cập nhật lúc: 10:35 17/05/2025
#6132 THPT Quốc giaVật lý
Trong thí nghiệm giao thoa sóng nước, hai nguồn sóng và cách nhau dao động theo phương vuông góc với mặt nước với cùng phương trình tính bằng . Tốc độ truyền sóng bằng và biên độ sóng không đổi trong quá trình truyền đi. Chọn hệ trục thuộc mặt phẳng mặt nước khi yên lặng, gốc O trùng với chứa đoạn . Phía trên mặt nước có một chất điểm chuyển động thẳng đều theo phương ngang với tốc độ sao cho hình chiếu P của nó xuống mặt nước chuyển động với phương trình quỹ đạo . Trong thời gian kể từ lúc P có tọa độ thì P cắt bao nhiêu vân cực đại trong vùng giao thoa sóng?
Lượt xem: 104,350 Cập nhật lúc: 22:47 16/05/2025
#7728 THPT Quốc giaToán
Trong không gian với hệ trục tọa độ , cho tứ diện có điểm , , , . Mặt phẳng cắt các cạnh lần lượt tại các điểm thỏa mãn . Biết tứ diện có thể tích nhỏ nhất. Mặt phẳng cắt trục hoành tại điểm , là phân số tối giản. Tính .
Lượt xem: 131,587 Cập nhật lúc: 13:48 17/05/2025
#8964 THPT Quốc giaToán
Trong không gian với hệ trục tọa độ , cho , , . Tìm tọa độ của vectơ .
Lượt xem: 152,563 Cập nhật lúc: 03:16 16/05/2025
#8130 THPT Quốc giaToán
Trong không gian với hệ trục toạ độ , cho ba điểm , . Biết , thể tích tứ diện bằng . Giá trị của biểu thức bằng
Lượt xem: 138,392 Cập nhật lúc: 10:28 17/05/2025
#8209 THPT Quốc giaToán
Trong không gian với hệ trục tọa độ . Cho tứ diện có điểm , , , . Trên các cạnh , , lần lượt lấy các điểm , , thỏa và có thể tích nhỏ nhất. Khi đó mặt phẳng đi qua điểm nào sau đây?
Lượt xem: 139,666 Cập nhật lúc: 10:37 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 40 phút
5,363 xem404 thi
