Mạch điện xoay chiều gồm có 3 hộp kín X,Y, W ghép nối tiếp với nhau, trong các hộp kín chỉ có thể là các linh kiện như điện trở thuần, cuộn dây thuần cảm và tụ điện. Các hộp kín có trở kháng phụ thuộc vào tần số như hình vẽ. Biết điện áp hiệu dụng hai đầu đoạn mạch là không đổi và bằng 200 V. Trong các hộp kín có một hộp kín có 1 tụ điện có điện dung $C = \frac{{{{10}^{ - 4}}}}{\pi }(F)$ và tại tần số f₁ công suất tiêu thụ của mạch điện là P = 160 W. Gọi tần số tại vị trí đồ thị (X) và (W) cắt nhau là f₃. Tính f₁ + f₃ ?

A.  

156,25 Hz.

B.  

131,25 Hz.

C.  

81,25 Hz.

D.  

100 Hz.

Đáp án đúng là: A

Nhận xét:

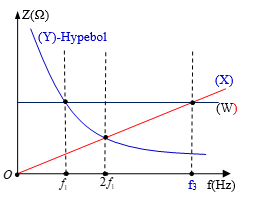
+ Hộp (W) có đồ thị trở kháng là một đường thẳng song song trục tần số f => Z_W không phụ thuộc tần số => (W) phải là một điện trở thuần R.

+ Hộp (X) là một đường thẳng đi qua gốc tọa độ=> Z_X=af, với a=const => (X) chỉ có thể là cuộn dây thuần cảm L. Với Z_X=Z_L

+ Hộp (Y) có dạng là một Hypebol=> phải có dạng Z_Y= a/f , => Y chỉ có thể là tụ điện với Z_Y=Z_C

Từ đồ thị ta thấy:

+ Tại f = f₁ ta có R=Z_C1

+ Tại f₂=2f₁ ta có:

${Z_{C2}} = \frac{{{Z_{C1}}}}{2} = \frac{R}{2};{Z_{L2}} = 2{Z_{L1}} \to 2{Z_{L1}} = \frac{{{Z_{C1}}}}{2} \to {Z_{L1}} = \frac{{{Z_{C1}}}}{4} = \frac{R}{4}$

+ Vậy: Khi f=f₁ hệ số công suất của mạch là:

$\cos \varphi = \frac{R}{Z} = \frac{R}{{\sqrt {{R^2} + {{(\frac{R}{4} - R)}^2}} }} = \frac{4}{5}$

+ Ta có: ${P_1} = U{I_1}\cos \varphi \to {I_1} = \frac{{{P_1}}}{{U\cos \varphi }} = \frac{{160}}{{200.\frac{4}{5}}} = 1A$

+ Điện trở R:

$R = \frac{{{P_1}}}{{{I_1}^2}} = \frac{{160}}{1} = 160\Omega = {Z_{C1}};{Z_{L1}} = \frac{R}{4} = \frac{{160}}{4} = 40\Omega$

+ Ta có :

${Z_{C1}} = \frac{1}{{2\pi {f_1}C}} \to {f_1} = \frac{1}{{2\pi {Z_{C1}}C}} = \frac{1}{{2\pi .160.\frac{{{{10}^{ - 4}}}}{\pi }}} = 31,25Hz$

${Z_{L1}}.{Z_{C1}} = 160.40 = 6400 = \frac{L}{C} \to L = 6400.\frac{{{{10}^{ - 4}}}}{\pi } = \frac{{16}}{{25\pi }} = \frac{{0,64}}{\pi }(H)$

+Khi (A) và (K) cắt nhau:

$R = {Z_{L3}} = 2\pi {f_3}L \to {f_3} = \frac{R}{{2\pi L}} = \frac{{160}}{{2\pi \frac{{16}}{{25\pi }}}} = 125Hz$

+ Tính: ${f_1} + {f_3} = 32,25 + 125 = 156,25Hz$