Trang chủ Đề thi Lớp 12 Toán 14486
thumbnail

Chuyên đề Toán 12 Bài 1: Mặt nón có đáp án

Khám phá bộ đề chuyên đề Toán 12 Bài 1 với chủ đề Mặt nón, được xây dựng trong khuôn khổ Chuyên đề 6: Mặt nón, mặt trụ, mặt cầu. Bộ đề này cung cấp các câu hỏi đa dạng, kèm đáp án chi tiết, giúp học sinh củng cố kiến thức về hình học không gian, nâng cao kỹ năng phân tích và tư duy logic. Đây là công cụ hữu ích hỗ trợ quá trình ôn tập và tự kiểm tra năng lực toán học của học sinh lớp 12, từ đó chuẩn bị tốt cho các kỳ thi quan trọng.

Từ khoá: chuyên đề Toán 12 mặt nón đáp án chuyên đề 6 mặt trụ mặt cầu ôn tập toán học sinh lớp 12 đề thi chuyên đề

Đề thi nằm trong bộ sưu tập: TOÁN 12

Số câu hỏi: 56 câuSố mã đề: 3 đềThời gian: 1 giờ

188,394 lượt xem 14,486 lượt làm bài


Chọn mã đề:


Bạn chưa làm Mã đề 1!!!

 

Xem trước nội dung:

Câu 1: 0.5 điểm

Cho hình nón N 1 có đỉnh S, chiều cao h. Một hình nón N 2 có đỉnh là tâm của đáy N 1 và có đáy là một thiết diện song song với đáy của N 2 như hình vẽ.

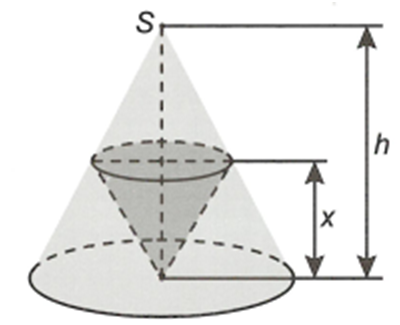
Hình ảnh

Khối nón N 2 có thể tích lớn nhất khi chiều cao x bằng

A.  
h 2
B.  
h 3
C.  
2 h 3
D.  
h 3 3
Câu 2: 0.5 điểm

Một bể nước lớn của khu công nghiệp có phần chứa nước là một khối nón đỉnh S phía dưới (hình vẽ), đường sinh SA = 27 mét. Có một lần lúc bể chứa đầy nước, người ta phát hiện nước trong bể không đạt yêu cầu về vệ sinh nên lãnh đạo khu công nghiệp cho thoát hết nước để làm vệ sinh bể chứa. Công nhân cho thoát nước ba lần qua một lỗ ở đỉnh S. Lần thứ nhất khi mực nước tới điểm M thuộc SA thì dừng, lần thứ hai khi mực nước tới điểm N thuộc SA thì dừng, lần thứ ba mới thoát hết nước. Biết rằng lượng nước mỗi lần thoát bằng nhau. Tính độ dài đoạn MN.

A.  
27 2 3 − 1 m
B.  
9 9 3 4 3 − 1 m
C.  
9 9 3 2 3 − 1 m
D.  
9 3 3 2 3 − 1 m
Câu 3: 0.5 điểm
Cho tứ diện đều ABCD có cạnh bằng a. Hình nón (N) có đỉnh A và đường tròn đáy là đường tròn ngoại tiếp tam giác BCD. Thể tích V của khối nón (N) là
A.  
V = π 3 a 3 27
B.  
V = 6 a 3 27
C.  
V = π 6 a 3 9
D.  
V = π 6 a 3 27
Câu 4: 0.5 điểm
Cho hình nón (N) có góc ở đỉnh bằng 60o. Mặt phẳng qua trục của (N) cắt (N) theo một thiết diện là tam giác có bán kính đường tròn ngoại tiếp bằng 2. Thể tích khối nón (2) là
A.  
V = 3 3 π
B.  
V = 4 3 π
C.  
V = 3 π
D.  
V = 6 π
Câu 5: 0.5 điểm
Xét các hình nón có đường sinh với độ dài đều bằng 10cm. Chiều cao của hình nón có thể tích lớn nhất là
A.  
5 3 cm
B.  
10 3 cm
C.  
5 3 3 cm
D.  
10 3 3 cm
Câu 6: 0.5 điểm
Cho hình lập phương ABCD.A'B'C'D' có thể tích bằng 1. Gọi (N) là một hình nón có tâm đường tròn đáy trùng với tâm của hình vuông ABCD, đồng thời các điểm A', B', C', D' nằm trên các đường sinh của hình nón như hình vẽ. Thể tích khối nón (N) có giá trị nhỏ nhất bằng
A.  
2 π 3
B.  
3 π 4
C.  
9 π 8
D.  
9 π 16
Câu 7: 0.5 điểm
Một tấm tôn hình tam giác đều SBC có độ dài cạnh bằng 3. K là trung điểm BC. Người ta dùng compa vạch một cung tròn MN có tâm là S, bán kính SK. Lấy phần hình quạt gò thành hình nón không có mặt đáy với đỉnh là S, cung MN thành đường tròn đáy của hình nón (hình vẽ). Tính thể tích khối nón trên.
Hình ảnh
A.  
π 105 64
B.  
3 π 32
C.  
3 π 3 32
D.  
π 141 64
Câu 8: 0.5 điểm
Cho khối gỗ hình trụ có bán kính 3 cm và chiều cao 6 cm, đáy là hai hình tròn tâm O và O'. Đục khối gỗ này tạo ra hai khối nón có đỉnh nằm trên OO' và đáy trùng với hai đáy của khối gỗ sao cho góc ở đỉnh bằng 60o (như hình vẽ) và O I = x 3 2 < x < 3 3 . Giá trị nhỏ nhất của tổng diện tích xung quanh hai hình nón đã đục bằng
A.  
12 π   c m 2
B.  
14 π   c m 2
C.  
44 π   c m 2
D.  
72 π   c m 2
Câu 9: 0.5 điểm
Cho hình nón có góc ở đỉnh bằng 60o, diện tích xung quanh bằng 6 π a 2 . Thể tích V của khối nón đã cho là
A.  
V = 3 π a 3 2 4
B.  
V = π a 3 2 4
C.  
V = 3 π a 3
D.  
V = π a 3
Câu 10: 0.5 điểm
Cắt một hình nón bởi một mặt phẳng qua trục ta được thiết diện là tam giác đều cạnh 2a. Tính diện tích toàn phần của hình nón đó.
A.  
6 π a 2
B.  
24 π a 2
C.  
3 π a 2
D.  
12 π a 2
Câu 11: 0.5 điểm
Cho tứ diện đều ABCD. Khi quay tứ diện đó quanh trục AB có bao nhiêu hình nón khác nhau được tạo thành?
A.  
Một.
B.  
Hai.
C.  
Không có hình nón nào.
D.  
Ba.
Câu 12: 0.5 điểm
Cho mặt cầu (S) bán kính R. Hình nón (N) thay đổi có đỉnh và đường tròn đáy thuộc mặt cầu (S). Thể tích lớn nhất của khối nón (N) là
A.  
32 π R 3 81
B.  
32 π R 3 27
C.  
32 π R 3 27
D.  
32 R 3 27
Câu 13: 0.5 điểm

Cho một tấm bìa có hình dạng tam giác vuông, biết b và c là độ dài hai cạnh góc vuông của tấm bìa. Trên tấm bìa đó ta chọn cạnh huyền làm trục rồi quay xung quanh tấm bìa đó (kể cả điểm trong) với trục tạo thành một khối tròn xoay. Thể tích V khối tròn xoay sinh ra bởi tấm bìa đó là

A.  
V = b 2 c 2 3 b 2 + c 2
B.  
V = π b 2 c 2 3 b 2 + c 2
C.  
V = 2 π b 2 c 2 3 b 2 + c 2
D.  
V = π b 2 c 2 3 2 b 2 + c 2
Câu 14: 0.5 điểm
Cho tứ diện đều ABCD có cạnh bằng a. Hình nón (N) có đỉnh A và đường tròn đáy là đường tròn ngoại tiếp tam giác BCD. Thể tích V của khối nón (N) là
A.  
V = π 3 a 3 27
B.  
V = 6 a 3 27
C.  
V = π 6 a 3 9
D.  
V = π 6 a 3 27
Câu 15: 0.5 điểm
Cho hình tứ diện ABCD có A D ⊥ A B C , ABC là tam giác vuông tại B. Biết B C = a ,   A B = a 3 ,   A D = 3 a . Quay các tam giác ABC và ABD (bao gồm cả điểm bên trong hai tam giác) xung quanh đường thẳng AB ta được hai khối tròn xoay. Thể tích phần chung của hai khối tròn xoay đó bằng:
A.  
3 3 π a 3 16
B.  
8 3 π a 3 3
C.  
5 3 π a 3 16
D.  
4 3 π a 3 16
Câu 16: 0.5 điểm
Cho mặt cầu (S) có bán kính R không đổi, hình nón (H) bất kì nội tiếp mặt cầu (S). Thể tích khối nón (H) là V1; và thể tích phần còn lại của khối cầu là V2. Giá trị lớn nhất của V 1 V 2 bằng
A.  
81 32
B.  
76 32
C.  
32 81
D.  
8 19
Câu 17: 0.5 điểm
Cho hình nón có đường sinh bằng đường kính đáy, diện tích đáy của hình nón bằng 9 π . Độ dài đường cao của hình nón bằng
A.  
3 3
B.  
3
C.  
9 3 2
D.  
3 3
Câu 18: 0.5 điểm
Giả sử đồ thị hàm số y = m 2 + 1 x 4 − 2 m x 2 + m 2 + 1 có 3 điểm cực trị là A, B, C mà x A < x B < x C . Khi quay tam giác ABC quanh cạnh AC ta được một khối tròn xoay. Giá trị của m để thể tích của khối tròn xoay đó lớn nhất thuộc khoảng nào trong các khoảng dưới đây?
A.  
(4;6)
B.  
(2;4)
C.  
(-2;0)
D.  
(0;2)
Câu 19: 0.5 điểm
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A'B'C'D'. Kết quả tính diện tích toàn phần S t p của khối nón đó có dạng bằng π a 2 4 b + c với b và c là hai số nguyên dương và b > 1. Giá trị của bc là
A.  
bc = 5
B.  
bc = 8
C.  
bc = 15
D.  
bc = 7
Câu 20: 0.5 điểm
Cho hình nón đỉnh S, đáy là đường tròn tâm O bán kính bằng 2a và độ dài đường sinh bằng a 5 . Mặt phẳng (P) qua đỉnh S cắt hình nón theo thiết diện là một tam giác có chu vi bằng 2 1 + 5 a . Khoảng cách d từ O đến mặt phẳng (P) là
A.  
d = a 3 3
B.  
d = a 2
C.  
d = a 3 7
D.  
d = a 3 2

Đề thi tương tự

Chuyên đề Toán 12 Bài 1: Nguyên hàm và phương pháp tìm nguyên hàm có đáp ánLớp 12Toán

1 mã đề 62 câu hỏi 1 giờ

184,36214,177

Chuyên đề Toán 12 Bài 1: Tính đơn điệu của hàm số có đáp ánLớp 12Toán

1 mã đề 151 câu hỏi 1 giờ

162,03512,454

Chuyên đề Toán 12 Bài 1: Lũy thừa - Hàm số lũy thừa có đáp ánLớp 12Toán

1 mã đề 58 câu hỏi 1 giờ

151,57311,654

Chuyên đề Toán 12 Bài 1: Khái niệm số phức có đáp ánLớp 12Toán

1 mã đề 19 câu hỏi 1 giờ

177,28413,633

Chuyên đề Toán 12 Bài 1: Hệ tọa độ trong không gian có đáp ánLớp 12Toán

3 mã đề 39 câu hỏi 1 giờ

171,39813,179

Chuyên đề Toán 12 Bài 1: Khái niệm về khối đa diện có đáp ánLớp 12Toán

1 mã đề 91 câu hỏi 1 giờ

188,92414,527

Chuyên đề Toán 12 Bài 2: Mặt trụ có đáp án - Đề cố định, Miễn phíLớp 12Toán

1 mã đề 51 câu hỏi 1 giờ

186,03414,305

Chuyên đề Toán 12 Bài 3: Mặt cầu - Khối cầu có đáp ánLớp 12Toán

2 mã đề 82 câu hỏi 1 giờ

165,30312,711

Chuyên đề Toán 12 Bài 3: Phương trình đường thẳng có đáp ánLớp 12Toán

5 mã đề 87 câu hỏi 1 giờ

153,95311,835