Chuyên đề Toán 12 Bài 3: Thể tích khối đa diện có đáp án

Chuyên đề Toán 12
Chuyên đề 5: Khối đa diện
Lớp 12;Toán

Thời gian làm bài: 1 giờ

Bạn chưa làm đề thi này!!!

Hãy bắt đầu chinh phục nào!

Xem trước nội dung:

Câu 1: 1 điểm

Cho hình chóp tam giác SABC là tam giác vuông tại A, AB = a, AC = 2a, cạnh bên SA vuông góc với mặt đáy và SA = a. Thể tích của khối chóp SABC là

A. $V = a^{3}$

V = \frac{7 a^{3}}{8} .

V = \frac{a^{3}}{3}

V = \frac{a^{3}}{4}

Câu 2: 1 điểm

Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy và ABCD. Thể tích của khối chóp SABCD là

A. $\frac{a^{3} \sqrt{2}}{3}$

a^{3} \sqrt{2}

\frac{a^{3} \sqrt{2}}{4}

\frac{a^{3} \sqrt{2}}{6}

Câu 3: 1 điểm

Cho hình chóp SABC đáy ABC là tam giác vuông tại B, AB = a, $\hat{A C B} = 60 °$ cạnh bên SA vuông góc với mặt phẳng đáy và SB tạo với mặt đáy một góc bằng $45 °$ . Thể tích của khối chóp SABC là

A. $\frac{a^{3} \sqrt{3}}{6}$

\frac{a^{3} \sqrt{3}}{18}

\frac{a^{3} \sqrt{3}}{9}

\frac{a^{3} \sqrt{3}}{12}

Câu 4: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình thang cân, $(A D ∥ B C)$ , cạnh AD = 2a, $A B = B C = C D = a$ và SA vuông góc với mặt phẳng (ABCD), cạnh SC tạo với mặt phẳng đáy góc $60 °$ . Thể tích của khối chóp SABCD là

A. $\frac{a^{3}}{3}$

\frac{a^{3} \sqrt{3}}{4}

\frac{3 a^{3} \sqrt{3}}{4}

\frac{3 a^{3} \sqrt{3}}{2}

Câu 5: 1 điểm

Cho hình chóp SABCD có đáy ABCD là tứ giác lồi AC = 2a, BD = 3a, $A C ⊥ B D$ và SA vuông góc với mặt phẳng (ABCD), cạnh SC tạo với mặt phẳng đáy góc $α$ thỏa mãn $\tan α = \frac{1}{3}$ . Thể tích khối chóp SABCD là

A. $\frac{2 a^{3}}{3}$

\frac{a^{3}}{3}

\frac{a^{3}}{4}

\frac{a^{3}}{12}

Câu 6: 1 điểm

Cho hình chóp SABC có SA vuông góc với mặt phẳng (ABC), hai mặt phẳng (SAB) và (SBC) vuông góc với nhau, $S B = a \sqrt{3}$ , $\hat{B S C} = 45 °$ , $\hat{A S B} = 30 °$ . Thể tích khối chóp SABC là V. Tỉ số $\frac{a^{3}}{V}$ là

A. $\frac{8}{3}$

\frac{8 \sqrt{3}}{3}

\frac{2 \sqrt{3}}{3}

\frac{4}{3}

Câu 7: 1 điểm

Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a, tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với (ABC). Thể tích khối chóp SABC là

\frac{a^{3}}{9}

\frac{a^{3} \sqrt{3}}{24}

\frac{a^{3} \sqrt{3}}{9}

\frac{a^{3}}{16}

Câu 8: 1 điểm

Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, cạnh BA = 3a, BC = 4a. Mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết $S B = 2 a \sqrt{3}$ và $\hat{S B C} = 30 °$ . Thể tích khối chóp SABC là

V = \sqrt{3} a^{3}

V = a^{3}

V = 3 \sqrt{3} a^{3}

V = 2 \sqrt{3} a^{3}

Câu 9: 1 điểm

Cho hình chóp SABCD có đáy là hình chữ nhật, AB = a, AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng $45 °$ . Thể tích của khối chóp SABCD là

\frac{a^{3} \sqrt{17}}{9}

\frac{a^{3} \sqrt{17}}{\sqrt{3}}

\frac{a^{3} \sqrt{17}}{6}

\frac{a^{3} \sqrt{17}}{3}

Câu 10: 1 điểm

Cho hình chóp SABCD có đáy ABCD, AB = a, $A D = a \sqrt{3}$ , tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, khoảng cách giữa AB và SC bằng $\frac{3 a}{2}$ . Tính thể tích V của khối chóp SABCD.

V = a^{3} \sqrt{3}

V = 2 a^{3} \sqrt{3}

V = \frac{2 a^{3} \sqrt{3}}{3}

V = 3 a^{3} \sqrt{3}

Câu 11: 1 điểm

Cho hình chóp SABCD có đáy ABC là tam giác vuông tại A, $A B = A \sqrt{2}$ , $A C = A \sqrt{5}$ . Hình chiếu của điểm S trên mặt phẳng (ABC) trùng với trung điểm của đoạn thẳng BC. Biết rằng góc giữa mặt phẳng (SAB) và mặt phẳng (SAC) bằng $60 °$ . Thể tích của khối chóp SABCD là

\frac{5 a^{3} \sqrt{6}}{12}

\frac{5 a^{3} \sqrt{10}}{12}

\frac{a^{3} \sqrt{210}}{24}

\frac{a^{3} \sqrt{30}}{12}

Câu 12: 1 điểm

Cho hình chóp SABC với các mặt phẳng $(S A B), (S B C), (S A C)$ vuông góc với nhau từng đôi một, diện tích các tam giác SAB, SBC, SAC lần lượt là $20 {cm}^{2}, 27 {cm}^{2}, 30 {cm}^{2}$ . Thể tích khối chóp SABC là

40 \sqrt{3} {cm}^{3}

40 {cm}^{3}

{60 cm}^{3}

60 \sqrt{3} {cm}^{3}

Câu 13: 1 điểm

Cho hình chóp SABCD có đáy là hình vuông cạnh a, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, biết $S C = a \sqrt{3}$ . Gọi M, N, P, Q lần lượt là trung điểm của SB, SD, CD, BC. Thể tích của khối chóp AMNPQ là

\frac{a^{3}}{3}

\frac{a^{3}}{8}

\frac{a^{3}}{12}

\frac{a^{3}}{4}

Câu 14: 1 điểm

Cho khối chóp tam giác đều SABC có cạnh đáy bằng a và cạnh bên bằng 2a. Thể tích của khối chóp SABC là

V = \frac{\sqrt{11} a^{3}}{12}

V = \frac{\sqrt{13} a^{3}}{12}

V = \frac{\sqrt{11} a^{3}}{6}

V = \frac{\sqrt{11} a^{3}}{4}

Câu 15: 1 điểm

Cho hình chóp tam giác đều SABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng $60 °$ . Thể tích khối chóp SABC là

V = \frac{a^{3} \sqrt{3}}{4}

V = \frac{a^{3} \sqrt{3}}{12}

V = \frac{a^{3} . \sqrt{5}}{12}

V = \frac{a^{3} . \sqrt{3}}{10}

Câu 16: 1 điểm

Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng a và cạnh bên tạo với mặt phẳng đáy một góc $60 °$ . Thể tích của khối chóp SABCD là

V = \frac{a^{3} \sqrt{6}}{2}

V = \frac{a^{3} \sqrt{6}}{3}

V = \frac{a^{3} \sqrt{3}}{2}

V = \frac{a^{3} \sqrt{6}}{6}

Câu 17: 1 điểm

Cho hình chóp tam giác đều SABC có cạnh đáy bằng a. Gọi G là trọng tâm tam giác ABC, góc giữa SG và mặt phẳng (SBC) là $30 °$ . Thể tích khối chóp SABC là

\frac{a^{3} \sqrt{3}}{4}

\frac{a^{3} \sqrt{3}}{8}

\frac{a^{3} \sqrt{3}}{12}

\frac{a^{3} \sqrt{3}}{24}

Câu 18: 1 điểm

Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là $a \sqrt{3}$ . Thể tích V của khối chóp đó là

V = \frac{2 \sqrt{2}}{3} a^{3}

V = \frac{4 \sqrt{2}}{3} a^{3}

V = \frac{\sqrt{2}}{6} a^{3}

V = \frac{\sqrt{2}}{9} a^{3}

Câu 19: 1 điểm

Cho hình chóp SABCcó đáy là tam giác vuông cân tại A, cạnh BC = 2a, gọi M là trung điểm BC, hình chiếu vuông góc của S lên mặt phẳng (ABC)là trung điểm của AM, tam giác SAM vuông tại S. Thể tích của khối chóp SABC là

A. $\frac{a^{3}}{6}$

\frac{a^{3}}{2}

\frac{a^{3}}{3}

\frac{a^{3}}{9}

Câu 20: 1 điểm

Cho hình chóp SABC, đáy là tam giác ABC có $A B = 19 cm$ , $B C = 20 cm$ , $A C = 37 cm$ , cạnh bên $SA= \sqrt{985} cm$ . Gọi M là trung điểm của BC, hình chiếu vuông góc của S lên mặt phẳng (ABC)là điểm H thỏa mãn $\vec{A H} = \frac{1}{3} \vec{A M}$ . Thể tích của khối chóp SABC là

570 {cm}^{3}

760 {cm}^{3}

1520 {cm}^{3}

1140 {cm}^{3}

Câu 21: 1 điểm

Cho hình chóp SABCD có đáy là hình chữ nhật cạnh AB = a, AD = 2a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AD. Cạnh SC tạo với đáy một góc bằng $30 °$ . Thể tích khối chóp SABCD là

A. $\frac{a^{3}}{3}$

\frac{2 a^{3} \sqrt{6}}{9}

\frac{a^{3} \sqrt{3}}{3}

\frac{a^{3} \sqrt{2}}{3}

Câu 22: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình chữ nhật tâm O, cạnh AB = a, $B C = a \sqrt{3}$ , tam giác SAC vuông tại S. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với trung điểm H của đoạn AO. Thể tích khối chóp SABC là

A. $\frac{a^{3}}{2}$

\frac{a^{3}}{4}

\frac{a^{3}}{6}

\frac{a^{3}}{8}

Câu 23: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh a,

\hat{B A C} = 60 °

, hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trọng tâm G của tam giác ABC. Mặt phẳng (SAC) hợp với mặt phẳng (ABCD) một góc

45 °

. Thể tích khối chóp SABCD là

A. $\frac{a^{3} \sqrt{3}}{12}$

\frac{a^{3}}{6}

\frac{a^{3}}{12}

\frac{a^{3} \sqrt{2}}{6}

Câu 24: 1 điểm

Cho hình chóp SABC, đáy ABC có $A B = 10 cm$ , $B C = 12 cm$ , $A C = 14 cm$ , các mặt bên cùng tạo với mặt phẳng đáy các góc bằng nhau và đều bằng $α$ thỏa mãn $\tan α = 3$ . Thể tích khối chóp SABCD là

228 {cm}^{3}

{576 cm}^{3}

{192 cm}^{3}

{384 cm}^{3}

Câu 25: 1 điểm

Cho chóp SABC có đáy ABC là tam giác đều cạnh bằng a, các cạnh bên bằng nhau và đều bằng $a \sqrt{3}$ . Thể tích khối chóp SABC là

A. $\frac{a^{3} \sqrt{3}}{2}$

\frac{a^{3} \sqrt{6}}{4}

\frac{a^{3} \sqrt{2}}{6}

\frac{a^{3} \sqrt{2}}{4}

Câu 26: 1 điểm

Cho hình chóp SABC có đáy ABC là tam giác cân $A B = A C = a$ , $\hat{B A C} = 120 °$ , các cạnh bên bằng nhau và cùng tạo với mặt phẳng đáy các góc $30 °$ . Thể tích khối chóp SABCD là

A. $\frac{a^{3} \sqrt{3}}{12}$

\frac{a^{3}}{4}

\frac{a^{3} \sqrt{3}}{4}

\frac{a^{3}}{12}

Câu 27: 1 điểm

Cho hình chóp SABCD có đáy ABCD là tứ giác lồi và góc tạo bởi các mặt phẳng (SAB), (SBC), (SCD), (SDA) với mặt đáy lần lượt là $90 °$ , $60 °$ , $60 °$ , $60 °$ . Biết rằng tam giác SAB vuông cân tại S, AB = a và chu vi tứ giác ABCD là 9a. Tính thể tích V của khối chóp SABCD.

A. $V = \frac{a^{3} \sqrt{3}}{9}$

V = \frac{a^{3} \sqrt{3}}{4}

V = \frac{2 a^{3} \sqrt{3}}{9}

V = a^{3} \sqrt{3}

Câu 28: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình chữ nhật cạnh AB = a, AD = 2a. Đỉnh S cách đều các đỉnh A, B, C, D, của mặt đáy và $S B = a \sqrt{5}$ . Thể tích khối chóp SABCD là

A. $\frac{a^{3} \sqrt{15}}{8}$

\frac{a^{3} \sqrt{15}}{6}

\frac{a^{3} \sqrt{15}}{4}

\frac{a^{3} \sqrt{15}}{3}

Câu 29: 1 điểm

Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a. Các mặt bên (SAB), (SAC), (SBC) lần lượt tạo với đáy các góc là $30 °$ , $45 °$ , $60 °$ . Tính thể tích của khối chóp SABC. Biết rằng hình chiếu vuông góc của S trên (ABC) nằm trong tam giác ABC.

V = \frac{a^{3} \sqrt{3}}{8 (4 + \sqrt{3})}

V = \frac{a^{3} \sqrt{3}}{4 + \sqrt{3}}

V = \frac{a^{3} \sqrt{3}}{4 (4 + \sqrt{3})}

V = \frac{a^{3} \sqrt{3}}{2 (4 + \sqrt{3})}

Câu 30: 1 điểm

Cho hình chóp SABC có đáy ABC là tam giác đều cạnh 2a, SA vuông góc với mặt phẳng (ABC), $S A = a \sqrt{3}$ . Thể tích khối chóp SABC là

a^{3}

2 a^{3}

6 a^{3}

12 a^{3}

Câu 31: 1 điểm

Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và AB = 3a, BC = 4a, AC = 5a, AD = 6a. Thể tích khối tứ diện ABCD là

6 a^{3}

12 a^{3}

18 a^{3}

36 a^{3}

Câu 32: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, cạnh SA vuông góc với mặt phẳng đáy, $S A = A B = a$ , $A D = 3 a$ . Gọi M là trung điểm cạnh BC. Thể tích khối chóp SABMD là

\frac{3 a^{3}}{4}

\frac{9 a^{3}}{4}

\frac{3 a^{3}}{2}

\frac{9 a^{3}}{2}

Câu 33: 1 điểm

Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại A, $B C = a \sqrt{2}$ , cạnh bên SA vuông góc với mặt phẳng đáy (ABC), mặt bên (SBC) tạo với mặt đáy (ABC) một góc bằng $45 °$ . Thể tích V của khối chóp SABC là

V = \frac{a^{3} \sqrt{2}}{4}

V = \frac{a^{3} \sqrt{2}}{12}

V = \frac{a^{3} \sqrt{2}}{6}

V = \frac{a^{3} \sqrt{3}}{18}

Câu 34: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và B cạnh $A B = B C = a$ , SA = a và vuông góc với mặt phẳng (ABCD). Khoảng cách từ D đến mặt phẳng (SAC) bằng $a \sqrt{2}$ . Thể tích V của khối chóp SABCD là

V = \frac{a^{3} \sqrt{3}}{4}

V = \frac{a^{3} \sqrt{3}}{6}

V = \frac{a^{3}}{2}

V = \frac{a^{3}}{3}

Câu 35: 1 điểm

Cho khối chóp SABCD có đáy ABCD là hình vuông cạnh $a \sqrt{3}$ , cạnh SA vuông góc với mặt phẳng (ABCD) và SB tạo với đáy một góc $60 °$ . Thể tích V của khối chóp SABCD là

V = 9 a^{3}

V = \frac{3 a^{3}}{4}

V = \frac{9 a^{3}}{2}

V = 3 a^{3}

Câu 36: 1 điểm

Cho khối chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và cạnh bên SB tạo với mặt phẳng đáy góc $45 °$ . Thể tích của khối chóp SABCD là

\frac{a^{3} \sqrt{2}}{3}

\frac{a^{3} \sqrt{2}}{6}

\frac{a^{3}}{3}

a^{3}

Câu 37: 1 điểm

Cho hình chóp SABC có đáy là tam giác vuông tại B, BC = 3a, $A C = a \sqrt{10}$ , cạnh bên SA vuông góc với đáy. Góc giữa mặt phẳng (SBC) và mặt phẳng đáy bằng $30 °$ . Thể tích khối chóp SABC là

\frac{a^{3} \sqrt{3}}{6}

\frac{a^{3} \sqrt{3}}{3}

\frac{a^{3} \sqrt{3}}{2}

a^{3} \sqrt{3}

Câu 38: 1 điểm

Cho tứ diện ABCD có $A C = A D = B C = C D = 2 a$ , cạnh bên BC vuông góc với mặt phẳng (ACD). Thể tích khối tứ diện là

a^{3} \sqrt{3}

2 a^{3} \sqrt{3}

\frac{a^{3} \sqrt{3}}{3}

\frac{2 a^{3} \sqrt{3}}{3}

Câu 39: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D, cạnh bên SD vuông góc với đáy, cho $A B = A D = a$ , $C D = 3 a$ , $S A = a \sqrt{3}$ . Thể tích khối chóp SABCD là

\frac{2 a^{3}}{3}

\frac{4 a^{3}}{3}

\frac{a^{3} \sqrt{2}}{3}

\frac{2 a^{3} \sqrt{2}}{3}

Câu 40: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D có $A B = 2 a$ , $A D = C D = a$ , $S A = a \sqrt{3}$ và SA vuông góc mặt phẳng đáy. Thể tích khối chóp SBCD bằng là

\frac{a^{3} \sqrt{3}}{6}

\frac{a^{3} \sqrt{3}}{2}

\frac{a^{3} \sqrt{3}}{3}

a^{3} \sqrt{3}

Câu 41: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy, cạnh SD = 2a. Thể tích của khối chóp SABCD là

\frac{a^{3} \sqrt{3}}{3}

\frac{a^{3} \sqrt{3}}{6}

\frac{a^{3} \sqrt{2}}{6}

\frac{a^{3} \sqrt{2}}{3}

Câu 42: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, cạnh SA vuông góc với đáy, $S B = a \sqrt{5}$ . Thể tích khối chóp SABCD là

\frac{a^{3} \sqrt{6}}{3}

\frac{2 a^{3}}{3}

2 a^{3}

\frac{a^{3}}{\sqrt{3}}

Câu 43: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh 2a, SA = a, $S B = a \sqrt{3}$ . Biết rằng $(S A B) ⊥ (A B C D)$ . Gọi M, N lần lượt là trung điểm của các cạnh AB, BC. Thể tích của khối chóp $S . B M D N$ là

\frac{a^{3} \sqrt{3}}{6}

\frac{a^{3} \sqrt{3}}{3}

2 a^{3} \sqrt{3}

\frac{a^{3} \sqrt{3}}{4}

Câu 44: 1 điểm

Thể tích của chóp tam giác đều có tất cả các cạnh đều bằng a là

\frac{a^{3} \sqrt{2}}{12}

\frac{a^{3} \sqrt{2}}{4}

\frac{a^{3} \sqrt{2}}{6}

\frac{a^{3} \sqrt{2}}{2}

Câu 45: 1 điểm

Cho hình chóp tứ giác đều SABCD có tất cả các cạnh bằng nhau, đường cao của một mặt bên là $a \sqrt{3}$ . Thể tích của khối chóp đó là

\frac{4 \sqrt{2}}{3} a^{3}

\frac{2 \sqrt{2}}{3} a^{3}

\frac{\sqrt{2}}{6} a^{3}

\frac{\sqrt{2}}{9} a^{3}

Câu 46: 1 điểm

Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng a và cạnh bên tạo với mặt phẳng đáy một góc $60 °$ . Tính thể tích V của khối chóp SABCD.

V = \frac{a^{3} \sqrt{6}}{2}

V = \frac{a^{3} \sqrt{6}}{3}

V = \frac{a^{3} \sqrt{3}}{2}

V = \frac{a^{3} \sqrt{6}}{6}

Câu 47: 1 điểm

Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 2a, cạnh bên bằng 3a. Thể tích V của khối chóp đã cho là

V = 4 \sqrt{7} a^{3}

V = \frac{4 \sqrt{7} a^{3}}{9}

V = \frac{4 a^{3}}{3}

V = \frac{4 \sqrt{7} a^{3}}{3}

Câu 48: 1 điểm

Cho hình chóp tam giác đều SABC có cạnh đáy bằng $a \sqrt{3}$ , cạnh bên bằng 2a. Tính thể tích V của khối chóp SABC.

V = \frac{a^{3} \sqrt{3}}{4}

V = \frac{3 a^{3} \sqrt{3}}{2}

V = \frac{3 a^{3} \sqrt{3}}{4}

V = \frac{3 a^{3}}{4}

Câu 49: 1 điểm

Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 2a, cạnh bên bằng 3a. Thể tích khối chóp SABCD là

\frac{8 a^{3}}{3}

\frac{a^{3} \sqrt{3}}{3}

\frac{4 a^{3}}{3}

\frac{2 a^{3}}{3}

Câu 50: 1 điểm

Một hình chóp tứ giác đều có đáy là hình vuông cạnh a, các mặt bên tạo với đáy một góc $α$ . Thể tích khối chóp đó là

\frac{a^{3}}{2} \sin α

\frac{a^{3}}{2} t a n α

\frac{a^{3}}{6} \cot α

\frac{a^{3}}{6} \tan α

Câu 51: 1 điểm

Cho hình chóp tứ giác đều SABCD, đáy ABCD có diện tích $16 {cm}^{2}$ , diện tích một mặt bên là $8 \sqrt{3} {cm}^{2}$ . Tính thể tích V của khối chóp SABCD.

V = \frac{32 \sqrt{2}}{3} {cm}^{3}

V = \frac{32 \sqrt{13}}{3} {cm}^{3}

V = \frac{32 \sqrt{11}}{3} {cm}^{3}

V = \frac{32 \sqrt{15}}{3} {cm}^{3}

Câu 52: 1 điểm

Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng $60 °$ . Gọi M là trung điểm của cạnh SD. Thể tích khối chóp MABC là

\frac{a^{3} \sqrt{3}}{24}

\frac{a^{3} \sqrt{2}}{2}

\frac{a^{3} \sqrt{2}}{4}

\frac{a^{3}}{8}

Câu 53: 1 điểm

Cho một hình chóp tứ giác đều có góc tạo bởi mặt bên và mặt đáy bằng $60 °$ và diện tích xung quanh bằng $8 a^{2}$ . Tính diện tích S của mặt đáy hình chóp.

4 a^{2} \sqrt{3}

4 a^{2}

2 a^{2}

2 a^{2} \sqrt{3}

Câu 54: 1 điểm

Cho hình chóp tứ giác đều SABCD có chiều cao h, góc ở đỉnh của mặt bên bằng $60 °$ . Thể tích của khối chóp SABCD là

\frac{3 h^{3}}{2}

\frac{h^{3}}{3}

\frac{2 h^{3}}{3}

\frac{h^{3} \sqrt{3}}{3}

Câu 55: 1 điểm

Cho hình chóp tứ giác SABCD đều có tất cả các cạnh bằng a. Thể tích khối chóp SABCD là

\frac{a^{3} \sqrt{2}}{3}

\frac{a^{3} \sqrt{2}}{6}

\frac{a^{3} \sqrt{2}}{9}

\frac{a^{3} \sqrt{2}}{12}

Câu 56: 1 điểm

Cho hình chóp SABC có đáy ABC là tam giác đều; mặt bên (SAB) nằm trong mặt phẳng vuông góc với mặt phẳng đáy và tam giác SAB vuông tại S, $S A = a \sqrt{3}$ , SB = a. Thể tích khối chóp SABC là

\frac{\sqrt{6} a^{3}}{6}

\frac{a^{3}}{2}

\frac{\sqrt{6} a^{3}}{3}

\frac{\sqrt{6} a^{3}}{2}

Câu 57: 1 điểm

Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, có BC = a; mặt bên (SAC) vuông góc với đáy, các mặt bên còn lại đều tạo với mặt đáy một góc $45 °$ . Thể tích khối chóp SABC là

\frac{a^{3}}{12}

a^{3}

\frac{a^{3}}{6}

\frac{a^{3}}{24}

Câu 58: 1 điểm

Cho hình chóp SABCD có đáy là hình thang vuông tại A và B, $A B = B C = a$ , AD = 2a. Hình chiếu của S lên mặt phẳng (ABCD) trùng với trung điểm cạnh AB. Biết rằng $S C = a \sqrt{5}$ . Tính theo a thể tích V của khối chóp SABCD.

\frac{a^{3} \sqrt{5}}{4}

\frac{a^{3} \sqrt{15}}{3}

\frac{a^{3} \sqrt{15}}{4}

\frac{2 a^{3} \sqrt{5}}{3}

Câu 59: 1 điểm

Cho hình chóp SABC có SA = a, tam giác ABC đều, tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp SABC là

\frac{\sqrt{6} a^{3}}{4}

\frac{\sqrt{6} a^{3}}{24}

\frac{\sqrt{6} a^{3}}{12}

\frac{\sqrt{6} a^{3}}{8}

Câu 60: 1 điểm

Cho tứ diện ABCD có $\hat{B A C} = \hat{C A D} = \hat{D A B} = 60 °$ , AB = a, AC = 2a, AD = 3a.Thể tích khối ABCD là.

\frac{\sqrt{2} a^{3}}{2}

\frac{3 \sqrt{2} a^{3}}{2}

3 \sqrt{2} a^{3}

\sqrt{2} a^{3}

Câu 61: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình chữ nhật. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết $S D = 2 a \sqrt{3}$ và góc tạo bởi đường thẳng SC và mặt phẳng (ABCD) bằng $30 °$ . Thể tích của khối chóp SABCD là

\frac{4 a^{3} \sqrt{6}}{3}

\frac{a^{3} \sqrt{6}}{13}

\frac{a^{3} \sqrt{3}}{4}

\frac{2 a^{3} \sqrt{3}}{7}

Câu 62: 1 điểm

Khối chóp SABCD đáy ABCD là hình bình hành. Lấy điểm M trên cạnh CD. Thể tích khối chóp SABCD bằng V. Thể tích khối chóp SABM là

\frac{V}{2}

\frac{V}{3}

\frac{2 V}{3}

\frac{V}{6}

Câu 63: 1 điểm

Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; AB = 6a,AC = 7a và AD = 4a. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích của tứ diện AMNP là

\frac{7 a^{3}}{2}

14 a^{3}

\frac{28 a^{3}}{3}

7 a^{3}

Câu 64: 1 điểm

Cho hình chóp SABCD có SA = x và tất cả các cạnh còn lại có độ dài bằng 18 cm. Có hai giá trị của x là $x_{1}; x_{2}$ thỏa mãn để thể tích của khối chóp SABCD bằng $972 \sqrt{2} {cm}^{3}$ . Tổng $x_{1}^{2} + x_{2}^{2}$ là

324

486

972

1296

Câu 65: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và B, $A B = B C = 4 a$ . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy, khoảng cách từ C đến mặt phẳng (SHD) bằng $a \sqrt{10}$ . Thể tích khối chóp SHBCD bằng

\frac{40 a^{3} \sqrt{3}}{3}

\frac{28 a^{3} \sqrt{3}}{3}

40 a^{3} \sqrt{3}

28 a^{3} \sqrt{3}

Câu 66: 1 điểm

Cho hình chóp tứ giác SABCD có $S A ⊥ (A B C D)$ , ABCD là hình thang vuông tại A và B biết AB = 2a, $A D = 3 B C = 3 a$ . Thể tích khối chóp SABCD theo a bằng bao nhiêu? Biết khoảng cách từ A đến mặt phẳng (SCD) bằng $\frac{3 \sqrt{6}}{4} a$ .

6 \sqrt{6} a^{3}

2 \sqrt{6} a^{3}

2 \sqrt{3} a^{3}

6 \sqrt{3} a^{3}

Câu 67: 1 điểm

Cho hình chóp SABCD có ABCD là hình thoi tâm O, $A B = a \sqrt{5}$ , AC = 4a, $S O = 2 \sqrt{2} a$ . Gọi M là trung điểm của SC. Biết SO vuông góc với mặt phẳng (ABCD). Thể tích khối chóp MOBC là

2 \sqrt{2} a^{3}

\sqrt{2} a^{3}

\frac{\sqrt{2} a^{3}}{3}

4 a^{3}

Câu 68: 1 điểm

Cho khối chóp SABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy, SA = 2a. Thể tích khối chóp SABCD là

V = 2 a^{3}

V = \frac{a^{3} \sqrt{15}}{12}

V = \frac{a^{3} \sqrt{15}}{6}

V = \frac{2 a^{3}}{3}

Câu 69: 1 điểm

Cho hình chóp SABCD có đáy ABC là tam giác đều cạnh 2a, cạnh SA tạo với mặt phẳng đáy một góc $60 °$ . Gọi G là trọng tâm tam giác ABC, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm của AG. Thể tích của khối chóp SABC là

2 a^{3} \sqrt{3}

a^{3} \sqrt{3}

\frac{a^{3} \sqrt{3}}{3}

\frac{2 a^{3} \sqrt{3}}{3}

Câu 70: 1 điểm

Cho hình chóp tứ giác SABCD, đáy là hình vuông cạnh $a \sqrt{2}$ . Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AC sao cho HC = 3HA, góc giữa SB với mặt phẳng đáy bằng $60 °$ .Thể tích khối chóp SABCD là

\frac{a^{3} \sqrt{15}}{6}

\frac{2 a^{3} \sqrt{15}}{3}

\frac{a^{3} \sqrt{15}}{9}

\frac{a^{3} \sqrt{15}}{3}

Câu 71: 1 điểm

Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, cạnh $A B = a \sqrt{3}$ , góc $\hat{A C B} = 60 °$ , hình chiếu vuông góc của S lên mặt phẳng (ABC) là trọng tâm tam giác ABC, gọi N là trung điểm của AC, góc giữa SN và mặt phẳng đáy là $30 °$ . Thể tích khối chóp SABC là

\frac{a^{3}}{6}

\frac{a^{3}}{18}

\frac{a^{3}}{9}

\frac{a^{3}}{12}

Câu 72: 1 điểm

Cho hình chóp SABCD có đáy là hình vuông cạnh a tâm O, hình chiếu của S lên mặt phẳng (ABC) là trung điểm của AO, góc giữa mặt phẳng (SCD) và (ABCD) bằng $60 °$ . Thể tích khối chóp SABCD là

\frac{3 a^{3} \sqrt{3}}{4}

\frac{a^{3} \sqrt{3}}{12}

\frac{a^{3} \sqrt{3}}{4}

\frac{a^{3} \sqrt{3}}{36}

Câu 73: 1 điểm

Cho hình chóp SABC có đáy ABC là tam giác vuông tại A có AC = a và BC = 2a. Mặt phẳng (SAC) tạo với mặt phẳng (ABC) một góc $60 °$ . Hình chiếu của S lên mặt phẳng (ABC) là trung điểm cạnh BC. Thể tích khối chóp SABC là

\frac{a^{3} \sqrt{3}}{4}

\frac{a^{3} \sqrt{3}}{8}

\frac{a^{3} \sqrt{3}}{12}

\frac{a^{3} \sqrt{3}}{2}

Câu 74: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = a. Hình chiếu vuông góc của S lên (ABCD) là điểm H thuộc AC và $A H = \frac{A C}{4}$ . Gọi CM là đường cao của tam giác SAC. Thể tích khối tứ diện SMBC là

\frac{a^{3} \sqrt{14}}{2}

\frac{a^{3} \sqrt{14}}{3}

\frac{a^{3} \sqrt{14}}{6}

\frac{a^{3} \sqrt{14}}{12}

Câu 75: 1 điểm

Cho hình chóp SABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho $\vec{H C} = 2 \vec{B H}$ . Biết cạnh SA hợp với mặt phẳng đáy một góc bằng $60 °$ .

\frac{a^{3}}{12}

\frac{a^{3} \sqrt{3}}{8}

\frac{a^{3}}{4}

\frac{a^{3} \sqrt{7}}{12}

Câu 76: 1 điểm

Cho hình chóp SABC biết rằng hình chiếu của S trên mặt phẳng đáy là điểm H thỏa mãn điều kiện hai điểm A và H nằm về hai phía so với đường thẳng BC đồng thời ba mặt phẳng (SAB), (SBC), (SCA) cùng tạo với mặt phẳng đáy các góc bằng nhau. Biết rằng tam giác ABC vuông tại A thỏa mãn điều kiện AB = 3, AC = 4 và khoảng cách từ H tới (SBC) bằng $\frac{12 \sqrt{13}}{13}$ . Thể tích của khối chóp SABC là

V = 8

V = 24

V = 12

V = 4

Câu 77: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh 10 cm, các mặt bên cùng tạo với mặt phẳng đáy các góc bằng nhau và đều bằng $α$ thỏa mãn $\tan α = \frac{9}{5}$ . Thể tích khối chóp SABCD là

600 {cm}^{3}

300 {cm}^{3}

900 {cm}^{3}

1200 {cm}^{3}

Câu 78: 1 điểm

Chóp tam giác đều SABC có đáy là tam giác đều cạnh bằng a, các cạnh bên tạo với đáy một góc $60 °$ . Thể tích của khối chóp là

\frac{a^{3} \sqrt{3}}{12}

\frac{a^{3} \sqrt{3}}{4}

\frac{3 a^{3} \sqrt{3}}{4}

\frac{a^{3} \sqrt{3}}{6}

Câu 79: 1 điểm

Cho hình chóp SABC có $A B = 5 cm$ , $B C = 6 cm$ , $C A = 7 cm$ . Hình chiếu vuông góc của S xuống mặt phẳng (ABC) nằm bên trong tam giác ABC. Các mặt phẳng (SAB), (SBC), (SCA) đều tạo với đáy một góc $60 °$ . Gọi AD, BE, CF là các đường phân giác của tam giác ABC với $D \in B C$ , $E \in A C$ , $F \in A B$ . Thể tích khối chóp SDEF là

\frac{280 \sqrt{6}}{143} {cm}^{3}

\frac{280 \sqrt{2}}{143} {cm}^{3}

\frac{280 \sqrt{3}}{143} {cm}^{3}

\frac{140 \sqrt{3}}{143} {cm}^{3}

Câu 80: 1 điểm

Cho hình lăng trụ đứng tam giác $A B C . A^{'} B^{'} C^{'}$ có tất cả các cạnh đều bằng a. Thể tích của khối lăng trụ $A B C . A^{'} B^{'} C^{'}$ là

\frac{3 a^{3}}{4} .

\frac{a^{3} \sqrt{3}}{4} .

\frac{3 a^{3} \sqrt{3}}{4} .

\frac{a^{3}}{4} .

Câu 81: 1 điểm

Cho hình lăng trụ đứng $A B C . A^{'} B^{'} C^{'}$ , đáy là tam giác ABC vuông tại A, $A B = a, \hat{A B C} = 30 °$ cạnh C'A hợp với mặt đáy góc $60 °$ .

Thể tích khối lăng trụ ABC.A'B'C' là

\frac{a^{3}}{6} .

\frac{a^{3}}{2} .

\frac{a^{3} \sqrt{3}}{6} .

\frac{a^{3} \sqrt{3}}{2} .

Câu 82: 1 điểm

Cho lăng trụ đứng $A B C . A^{'} B^{'} C^{'}$ , đáy ABC là tam giác vuông tại A, cạnh $A C = a, \hat{A B C} = 30 °$ , cạnh BC' hợp với mặt bên (ACC'A) góc $30 °$ . Thể tích khối lăng trụ $A B C . A^{'} B^{'} C^{'}$ bằng

a^{3} \sqrt{6} .

\frac{a^{3} \sqrt{6}}{3} .

2 a^{3} \sqrt{3} .

\frac{a^{3} \sqrt{3}}{3} .

Câu 83: 1 điểm

Cho lăng trụ đều ABC.A'B'C' có cạnh đáy bằng a và

A B^{'} ⊥ B C^{'}

. Thể tích của khối lăng trụ ABC.A'B'C' là

V = \frac{7 a^{3}}{8} .

V = a^{3} \sqrt{6} .

V = \frac{a^{3} \sqrt{6}}{8} .

V = \frac{a^{3} \sqrt{6}}{4} .

Câu 84: 1 điểm

Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, cạnh $B C = a \sqrt{2}$ , góc giữa hai đường thẳng AC' và BA' bằng $60 °$ . Thể tích khối lăng trụ ABC.A'B'C' là

\frac{a^{3} \sqrt{3}}{2} .

\frac{a^{3}}{2} .

\frac{a^{3} \sqrt{3}}{3} .

\frac{a^{3}}{3} .

Câu 85: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C'có đáy ABC là tam giác vuông, AB = BC = a. Biết rằng góc giữa hai mặt phẳng (ACC')và (AB'C')bằng $60 °$ . Thể tích khối chóp $B^{'} . A C C^{'} A^{'}$ bằng

\frac{a^{3}}{3} .

\frac{a^{3}}{6} .

\frac{a^{3}}{2} .

\frac{a^{3} \sqrt{3}}{3} .

Câu 86: 1 điểm

Cho lăng trụ ABC.A'B'C' tam giac ABC vuông cân tại A, cạnh $A A^{'} = a \sqrt{3}$ , hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trong điểm của AC, góc tạo bởi AA' với (ABC) bằng $45 °$ . Thể tích khối lăng trụ ABC.A'B'C' là

\frac{3 a^{3} \sqrt{6}}{2} .

\frac{a^{3} \sqrt{6}}{3} .

\frac{a^{3} \sqrt{3}}{4} .

a^{3} \sqrt{6} .

Câu 87: 1 điểm

Cho lăng trụ ABC.A'B'C' đây là tam giác ABC vuông tại A, $A B = a, B C = a \sqrt{3}$ , hình chiếu vuông góc của B' trên mặt phẳng (ABC) trùng với chân đường cao H kẻ từ đỉnh A của tam giác ABC, góc tạo bởi AB' với (ABC) bằng $60 °$ . Thể tích khối lăng trụ ABC.A'B'C' là

\frac{\sqrt{3} a^{3}}{4} .

\frac{3 \sqrt{3} a^{3}}{4} .

\frac{a^{3}}{3} .

a^{3} .

Câu 88: 1 điểm

Cho lăng trụ ABCD.A'B'C'D' đáy là hình thang cân ABCD có $A C ⊥ B D, A C = 2 a$ , cạnh AA' tạo với mặt phẳng đáy góc $60 °$ . Hình chiếu vuông góc của A' trên mặt phẳng (ABCD) là điểm H thuộc đoạn AC sao cho $A H = \frac{1}{3} H C$ . Thể tích của khối lăng trụ ABCD.A'B'C'D' là

\frac{2 a^{3} \sqrt{3}}{3} .

2 a^{3} \sqrt{3} .

\frac{a^{3} \sqrt{3}}{3} .

a^{3} \sqrt{3}

Câu 89: 1 điểm

Cho khối lăng trụ ABC.A'B'C' , khoảng cách từ C đến đường thẳng BB' bằng 2, khoảng cách từ A đến các đường thẳng BB' và CC' lần lượt bằng 1 và $\sqrt{3}$ , hình chiếu vuông góc A lên mặt phẳng (A'B'C') là trung điểm M của B'C' và $A^{'} M = 2$ . Thể tích của khối lăng trụ ABC.A'B'C' bằng

\sqrt{3} .

\frac{2 \sqrt{3}}{3} .

Câu 90: 1 điểm

Cho hình lập phương ABCD.A'B'C'D' có $A^{'} C = 4 \sqrt{3}$ .Thể tích khối lập phương ABCD.A'B'C'D' là

2 \sqrt{3} .

4 \sqrt{3} .

64.

125.

Câu 91: 1 điểm

Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, $\hat{B A D} = 120 °$ .Gọi G là trọng tâm tam giác ABD, góc tạo bởi C'G và mặt đáy bằng $30 °$ . Thể tích khối hộp ABCD.A'B'C'D' là

a^{3} .

\frac{a^{3}}{3} .

\frac{a^{3}}{6} .

\frac{a^{3}}{12} .

Câu 92: 1 điểm

Một tấm bìa hình vuông có cạnh 50cm. Người ta cắt bỏ đi ở một góc tấm bìa hình vuông cạnh 16cm rồi gấp lại thành một cái hộp chữ nahat không có nắp. Thể tích khối hộp chữ nhật là

5184

c m^{3} .

8704

c m^{3} .

4608

c m^{3} .

18496

c m^{3} .

Câu 93: 1 điểm

Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật $A B = \sqrt{15},$ AD = 5. Hai mặt bên (ABB'A')và (ADD'A')lần lượt tạo với mặt phẳng đáy những góc $30 °$ và $60 °$ , cạnh bên có độ dài bằng 1. Thể tích khối hộp ABCD.A'B'C'D'là

21.

\frac{15 \sqrt{65}}{12} .

\frac{15 \sqrt{65}}{13} .

\frac{\sqrt{21}}{2} .

Câu 94: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C', đáy là tam giác ABC vuông cân tại A, $B C = 2 a, A' B = a \sqrt{3}$ . Thể tích khối lăng trụ ABC.A'B'C' là

\frac{a^{3}}{2} .

a^{3} .

3 a^{3} .

\frac{a^{3}}{3} .

Câu 95: 1 điểm

Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Đường thẳng AB' hợp với đáy một góc $60 °$ . Tính thể tích của khối lăng trụ ABC.A'B'C' là

V = \frac{3 a^{3}}{2} .

V = \frac{a^{3}}{4} .

V = \frac{3 a^{3}}{4} .

V = \frac{a^{3}}{2} .

Câu 96: 1 điểm

Cho hình lăng trụ đứng tam giác ABC.A'B'C' có $A B = 26 c m, B C = 60 c m, A C = 74 c m$ , diện tích xung quanh bằng 2880cm2. Thể tích của khối lăng trụ ABC.A'B'C' là

4320

c m^{3}

3840

c m^{3}

12960

c m^{3}

11520

c m^{3}

Câu 97: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C', có đáy ABC là tam giác vuông cân tại A, $A A^{'} = 2 a,$ $A^{'} B = 3 a$ . Thể tích khối lăng trụ ABC.A'B'C' là

5 a^{3} .

13 a^{3} .

\frac{5 a^{3}}{2} .

\frac{13 a^{3}}{2} .

Câu 98: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C' có $A B = a, A C = 2 a, \hat{B A C} = 120 °$ , cạnh C'A hợp với mặt đáy góc $45 °$ . Thể tích khối lăng trụ ABC.A'B'C' là

\frac{2 a^{3} \sqrt{3}}{3} .

2 a^{3} \sqrt{3} .

\frac{a^{3} \sqrt{3}}{3} .

a^{3} \sqrt{3}

Câu 99: 1 điểm

Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân, $A B = A C = a, \hat{B A C} = 120 °$ . Mặt phẳng (AB'C') tạo với mặt đáy góc $30 °$ . Tính thể tích lăng trụ ABC.A'B'C' bằng V. Tỷ số $\frac{a^{3}}{V}$ có giá trị là

\frac{8}{3} .

\frac{4}{3} .

Câu 100: 1 điểm

Cho khối lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh đều bằng a. Thể tích khối tứ diện AA'BC' là

\frac{a^{3}}{2} .

\frac{a^{3} \sqrt{3}}{2} .

\frac{a^{3} \sqrt{3}}{4} .

\frac{a^{3} \sqrt{3}}{12} .

Câu 101: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, góc giữa hai đường thẳng AB' và BC' bằng $60 °$ . Thể tích khối lăng trụ ABC.A'B'C' là

\frac{a^{3} \sqrt{3}}{2} .

\frac{a^{3} \sqrt{6}}{3} .

\frac{a^{3} \sqrt{3}}{4} .

\frac{a^{3} \sqrt{6}}{4} .

Câu 102: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông cân tại A, cạnh $B C = a \sqrt{6}$ . Góc giữa mặt phẳng (AB'C) và mặt phẳng $(B C C B^{'})$ bằng $60 °$ . Thể tích của khối đa diện $A B^{'} C A^{'} C^{'}$ là

\frac{3 a^{3} \sqrt{3}}{2} .

a^{3} \sqrt{3} .

\frac{a^{3} \sqrt{3}}{2} .

\frac{a^{3} \sqrt{3}}{3} .

Câu 103: 1 điểm

Cho hình lăng trụ ABC.A'B'C' có đáy là một tam giác đều cạnh a. Góc giữa cạnh bên và mặt phẳng đáy bằng $30 °$ . Hình chiếu của đỉnh A' trên mặt phẳng đáy (ABC) trùng với trung điểm cạnh BC. Thể tích khối đa diện $A B A^{'} B^{'} C^{'}$ là

\frac{a^{3} \sqrt{3}}{4} .

\frac{a^{3} \sqrt{3}}{3} .

\frac{a^{3} \sqrt{3}}{12} .

\frac{a^{3} \sqrt{3}}{12} .

Câu 104: 1 điểm

Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A' xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên $(A A^{'} C^{'} C)$ tạo với đáy một góc bằng $45 °$ . Thể tích của khối đa diện $A B C A^{'} B^{'}$ là

\frac{a^{3}}{6} .

\frac{3 a^{3}}{4} .

\frac{3 a^{3}}{8} .

\frac{a^{3}}{4} .

Câu 105: 1 điểm

Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại C, $A C = 6 a, B C = 8 a$ , hình chiếu vuông góc của C' lên mặt phẳng (ABC) là trung điểm của BC , góc tạo bởi hai mặt phẳng $(C^{'} A C)$ và (ABC) bằng $60 °$ . Thể tích khối lăng trụ ABC.A'B'C' là

128 a^{3} \sqrt{3} .

64 a^{3} \sqrt{3} .

96 a^{3} \sqrt{3} .

32 a^{3} \sqrt{3} .

Câu 106: 1 điểm

Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng $\frac{a \sqrt{3}}{4}$ . Thể tích của khối lăng trụ ABC.A'B'C' là

\frac{a^{3} \sqrt{3}}{6} .

\frac{a^{3} \sqrt{3}}{12} .

\frac{a^{3} \sqrt{3}}{3} .

\frac{a^{3} \sqrt{3}}{24} .

Câu 107: 1 điểm

Cho lăng trụ tam giác ABC.A'B'C' có BB' = a, góc giữa đường thẳng BB' và (ABC) bằng $60 °$ , tam giác ABC vuông tại C và góc $\hat{B A C} = 60 °$ . Hình chiếu vuông góc của điểm B' lên (ABC) trùng với trọng tâm của $Δ A B C$ . Thể tích của khối tứ diện A'ABC là

\frac{13 a^{3}}{108} .

\frac{7 a^{3}}{106} .

\frac{15 a^{3}}{108} .

\frac{9 a^{3}}{208}

Câu 108: 1 điểm

Cho lăng trụ tam giác ABC.A'B'C' có độ dài cạnh bên bẳng 4 và khoảng cách từ điểm A đến các đường thẳng BB', CC' lần lượt bẳng 1 và 2. Biết góc giữa hai mặt phẳng $(A B B^{'} A^{'})$ và $(A C C^{'} A^{'})$ bằng $60 °$ . Thể tích khối lăng trụ ABC.A'B'C' là

4 \sqrt{3} .

\sqrt{3} .

3 \sqrt{3} .

2 \sqrt{3} .

Câu 109: 1 điểm

Cho lăng trụ tam giác ABC.A'B'C' có đáy là tam giác vuông tại A có $A B = 1; B C = 2$ . Góc $\hat{C B B^{'}} = 90 °; \hat{A B B^{'}} = 120 °$ . Gọi M là trung điểm cạnh AA' . Biết $d (A B^{'}, C M) = \frac{\sqrt{7}}{7}$ . Thể tích khối lăng trụ ABC.A'B'C' là

2 \sqrt{2} .

\frac{4 \sqrt{2}}{9} .

4 \sqrt{2} .

\frac{4 \sqrt{2}}{3} .

Câu 110: 1 điểm

Cho lăng trụ xiên tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh dài 20cm. Hình chiếu của A' xuống mặt đáy là tâm đường tròn ngoại tiếp tam giác ABC biết AA' hợp với đáy một góc $45 °$ . Thể tích khối lăng trụ ABC.A'B'C' là

1000 \sqrt{3} m^{3} .

2000 m^{3} .

2000 \sqrt{3} m^{3} .

1000 m^{3} .

Câu 111: 1 điểm

Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, $\hat{B A D} = 60 °$ . Hình chiếu vuông góc của A' lên mặt phẳng (ABCD) là điểm H thuộc AB thỏa mãn $A H = \frac{B H}{2}, \hat{A^{'} A H} = 30 °$ . Thể tích khối hộp ABCD.A'B'C'D' là

\frac{a^{3}}{6} .

\frac{a^{3}}{2} .

\frac{a^{3} \sqrt{3}}{6} .

\frac{a^{3} \sqrt{3}}{2} .

Câu 112: 1 điểm

Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình bình hành có $A B = a, A D = 3 a, \hat{B A D} = 120 °$ , $A A^{'} = \sqrt{3} a$ , hình chiếu vuông góc của A' lên mặt phẳng (ABCD) là trọng tâm tam giác ABD. Thể tích khối hộp ABCD.A'B'C'D' là

\frac{a^{3} \sqrt{5}}{2} .

\frac{2 a^{3} \sqrt{5}}{3} .

a^{3} \sqrt{15} .

2 a^{3} \sqrt{5} .

Câu 113: 1 điểm

Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông có đường chéo $A C = 8 c m$ , cạnh $A^{'} C = 10 c m$ . Thể tích khối hộp ABCD.A'B'C'D' là

144 \sqrt{2} c m^{3} .

192 \sqrt{2} c m^{3} .

144 c m^{3} .

192 c m^{3} .

Câu 114: 1 điểm

Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi có $A C = 6 a, B D = 8 a$ . Chu vi của một đáy bẳng 4 lần chiều cao khối hộp.Thể tích khối hộp ABCD.A'B'C'D' là

40 a^{3} .

80 a^{3} .

240 a^{3} .

120 a^{3} .

Câu 115: 1 điểm

Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi, $\hat{B A D} = 60 °$ , $A C = B D^{'} = 2 \sqrt{3}$ . Thể tích khối hộp ABCD.A'B'C'D' là

2 \sqrt{3} .

4 \sqrt{3} .

4 \sqrt{6} .

\sqrt{6} .

Câu 116: 1 điểm

Cho hình hộp đứng ABCD.A'B'C'D' có đáy là hình vuông, canh biên AA' = 3a và đường chéo $A C^{'} = 5 a$ . Thể tích V của khối hộp ABCD.A'B'C'D là

V = a^{3} .

V = 16 a^{3} .

V = 8 a^{3} .

V = 24 a^{3} .

Câu 117: 1 điểm

Một hình hộp đứng có đáy là hình thoi cạnh a, góc nhọn $60 °$ và đường chéo lớn của đáy bẳng đường chéo nhỏ của hình hộp. Thể tích của khối hộp đó là

a^{3} .

a^{3} \sqrt{3} .

\frac{a^{3} \sqrt{3}}{2}

\frac{a^{3} \sqrt{6}}{2} .

Câu 118: 1 điểm

Cho một hình hộp đứng ABCD.A'B'C'D'đáy ABCD là hình vuông cạnh 15cm và đường chéo BD'với đáy ABCD một góc $30 °$ . Thể tích khối hộp ABCD.A'B'C'D'gần nhất giá trị nào trong các giá trị sau?

1949

c m^{3} .

1125

c m^{3} .

1591

c m^{3} .

2756

c m^{3} .

Câu 119: 1 điểm

Cho hình hộp đứng ABCD.A'B'C'D' có đáy là hình vuông cạnh a. Khoảng cách từ điểm A đến mặt phẳng $(A^{'} B C D^{'})$ bẳng $\frac{a \sqrt{3}}{2}$ . Thể tích hình hộp ABCD.A'B'C'D' là

V = a^{3} \sqrt{3},

V = \frac{a^{3} \sqrt{21}}{7} .

V = a^{3} .

V = \frac{a^{3} \sqrt{3}}{3}

Câu 120: 1 điểm

Cho hình lập phương ABCD.A'B'C'D' có diện tích tam giác ACD' bẳng $a^{2} \sqrt{3}$ . Thể tích của hình lập phương ABCD. A'B'C'D' là

V = 3 \sqrt{3} a^{3} .

V = 2 \sqrt{6} a^{3} .

V = 8 a^{3} .

V = 2 \sqrt{2} a^{3} .

Câu 121: 1 điểm

Cho khối hộp chữ nhật ABCD.A'B'C'D' có $A D = 2 A B, B D^{'} = \sqrt{10} a$ , cạnh A'C hợp với đáy một góc $45 °$ . Thể tích khối hộp chữ nhật ABCD.A'B'C'D' là

\frac{2 \sqrt{5} a^{3}}{3} .

\frac{a^{3} \sqrt{10}}{3} .

\frac{2 a^{3} \sqrt{10}}{3} .

2 \sqrt{5} a^{3} .

Câu 122: 1 điểm

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và AC. Khi đó tỉ số thể tích của khối tứ diện AMND và khối tứ diện ABCD là

\frac{1}{2}

\frac{1}{4}

\frac{1}{6}

\frac{1}{8}

Câu 123: 1 điểm

Cho hình chóp SABC, trên các cạnh AB, BC, SC lần lượt lấy các điểm M, N, P sao cho $A M = 2 M B, B N = 4 N C, S P = P C$ . Tỉ số thể tích của hai khối chóp S.BMN và A.CPN là

\frac{4}{3}

\frac{8}{3}

\frac{5}{6}

Câu 124: 1 điểm

Cho hình chóp tứ giác đều SABCD có đáy là hình vuông ABCD cạnh a, góc giữa mặt bên và mặt phẳng đáy là $α$ thỏa mãn $\cos α = \frac{1}{3}$ . Mặt phẳng (P) qua AC và vuông góc với mặt phẳng (SAD) chia khối chóp SABCD thành hai khối đa diện có thể tích là $V_{1}$ và $V_{2}$ với $V_{1} < V_{2}$ . Tỉ lệ $\frac{V_{1}}{V_{2}}$ gần nhất với giá trị nào trong các giá trị sau?

0,11.

0,13.

0,7.

0,9.

Câu 125: 1 điểm

Cho hình chóp SABC có $S A = S B = a; S C = 2 a, \hat{ASB} = \hat{BSC} {=60}^{0}, \hat{ASC} = 90^{0}$ . Thể tích của khối chóp SABCbằng V. Tỉ số $\frac{6 V}{a^{3}}$ bằng

\frac{4 \sqrt{6}}{3}

\sqrt{2}

\sqrt{3}

\frac{\sqrt{3}}{3}

Câu 126: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình bình hành. Trên các cạnh SA, SB, SC lần lượt lấy các điểm A',B',C' sao cho $S A = 2 S A^{'}; S B = 3 S B^{'}; S C = 4 S C^{'}$ , mặt phẳng (A'B'C') cắt cạnh SD tại D'. Gọi $V_{1}, V_{2}$ lần lượt là thể tích của hai khối chóp $S . A^{'} B^{'} C^{'} D^{'}$ và SABCD. Khi đó tỉ số $\frac{V_{1}}{V_{2}}$ bằng

\frac{1}{24}

\frac{1}{26}

\frac{7}{12}

\frac{7}{24}

Câu 127: 1 điểm

Cho khối lăng trụ ABC.A'B'C' có M, N, P lần lượt thuộc các cạnh AA' $, B B^{'}, C C^{'}$ sao cho $A M = M A^{'}, B N = 3 N B^{'}, C P = 3 P C^{'}$ . Đặt $V_{1}$ là thể tích của khối đa diện $A B C M N P, V_{2}$ là thể tích khối đa diện còn lại. Tỉ số $\frac{V_{1}}{V_{2}}$ là

\frac{3}{2}

\frac{4}{3}

Câu 128: 1 điểm

Cho hình lăng trụ tam giác ABC.A'B'C' có thể tích là V và độ dài cạnh bên AA' = 6. Trên cạnh $A^{'} A, B^{'} B, C^{'} C$ lần lượt lấy các điểm M, N, P sao cho $A M = 2, B N = x, C P = y$ với x, y là các số dương thỏa mãn xy =12. Biết rằng thể tích khối đa diện $A B C . M N P$ bằng $\frac{1}{2} V$ . Giá trị của $x^{2} + y^{2}$ bằng

Câu 129: 1 điểm

Cho hình lập phương ABCD.A'B'C'D' có N là trung điểm CC'. Mặt phẳng $(α)$ đi qua AN cắt các cạnh BB',DD' lần lượt tại M, P. $(α)$ chia khối lập phương thành hai phần có thể tích tương ứng bằng $V_{1}$ và $V_{2} (V_{1} < V_{2})$ . Tỉ số $\frac{V_{2}}{V_{1}}$ bằng

\frac{7}{3}

\frac{5}{2}

Câu 130: 1 điểm

Cho hình hộp ABCD.A'B'C'D' có thể tích bằng $36 c m^{3}$ . Gọi hai điểm M, N lần lượt thuộc các cạnh AA', CC' sao cho $A M = 2 A^{'} M, C N = 3 C^{'} N$ . Một mặt phẳng đi qua M, N lần lượt cắt cạnh BB', DD' tại P và Q. Thể tích khối $A B C D M P N Q$ bằng

18 c m^{3}

22 c m^{3}

10, 5 c m^{3}

25, 5 c m^{3}

Câu 131: 1 điểm

Cho hình hộp ABCD.A'B'C'D' có thể tích bằng V. Gọi M, N, P lần lượt thuộc các cạnh $A A^{'}, B B^{'}, C C^{'},$ sao cho $A M = 2 A^{'} M,2 B N = 3 B^{'} N; 3 C P = 4 C^{'} P; 4 D Q = 5 D^{'} Q$ . Thể tích khối $A B C D M N P Q$ bằng

\frac{572 V}{945}

\frac{13 V}{21}

\frac{26 V}{45}

\frac{559 V}{945}

Câu 132: 1 điểm

Một khúc gỗ có dạng và độ dài các cạnh được cho như hình vẽ. Thể tích khúc gỗ là

V = 12.

V = 96.

V = 36.

V = 24.

Câu 133: 1 điểm

Một hình hộp chữ nhật ABCD.A’B’C’D’ có ba kích thước là 2 cm, 3 cm và 6 cm. Thể tích của khối tứ diện A.CB’D’ bằng

8 c m^{3}

12 c m^{3}

16 c m^{3}

4 c m^{3}

Câu 134: 1 điểm

Cho hình lăng trụ đứng ABC.A’B’C’ có thể tích bằng V. Gọi M, N, P lần lượt là các điểm nằm trên các cạnh AA’, BB’, CC’ sao cho AM = $\frac{1}{2}$ AA’; BN = $\frac{2}{3}$ BB’; CP = $\frac{3}{4}$ CC’. Thể tích khối chóp M.BCPN là

\frac{7 V}{36}

\frac{17 V}{36}

\frac{7 V}{18}

\frac{11 V}{18}

Câu 135: 1 điểm

Cho hình chóp S.ABCD có đáy là hình bình hành. Hai cạnh AC, BD cắt nhau tại O. Mặt phẳng (P) đi qua điểm O và song song với mặt phẳng (SAD) cắt khối chóp S.ABCD tạo thành hai khối có thể tích lần lượt là $V_{1}$ ; $V_{2} (V_{1} < V_{2})$ . Tỉ số $\frac{V_{1}}{V_{2}}$ bằng

\frac{5}{11}

\frac{3}{5}

\frac{7}{13}

\frac{1}{2}

Câu 136: 1 điểm

Cho hình lập phương ABCD.A’B’C’D’ cạnh 2a, gọi M là trung điểm của BB’ và P thuộc cạnh DD’ sao cho $D P = \frac{1}{4} DD'$ . Mặt phẳng (AMP) cắt CC’ tại N. Thể tích khối đa diện AMNPBCD bằng

V = 2 a^{3}

V = 3 a^{3}

V = \frac{9 a^{3}}{4}

V = \frac{11 a^{3}}{3}

Câu 137: 1 điểm

Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N lần lượt là trung điểm các cạnh AB và BC. Điểm P trên cạnh CD sao cho PD=2CP. Mặt phẳng (MNP) cắt AD tại Q. Thể tích khối đa diện BMNPQD bằng

\frac{\sqrt{2}}{16}

\frac{25 \sqrt{2}}{432}

\frac{\sqrt{2}}{48}

\frac{13 \sqrt{2}}{432}

Câu 138: 1 điểm

Cho khối lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác đều cạnh a. Cạnh AA’=2a và tạo với đáy một góc $45^{\circ}$ . Thể tích khối tứ diện ACA’B’ là

\frac{a^{3} \sqrt{6}}{12}

\frac{a^{3} \sqrt{6}}{8}

\frac{a^{3} \sqrt{6}}{4}

\frac{a^{3} \sqrt{6}}{6}

Câu 139: 1 điểm

Cho lăng trụ ABC.A’B’C’ có thể tích bằng 15. Gọi M, N, P lần lượt là các điểm trên cạnh A’B’, B’C’, BC sao cho M là trung điểm của A’B’, B’N= $\frac{4}{5} B' C'$ và BP= $\frac{3}{5} B C$ . Đường thẳng NP cắt đường thẳng BB’ tại E và đường thẳng EM cắt đường thẳng AB tại Q. Thể tích khối đa diện lồi AQPCA’MNC’ bằng

\frac{23}{64}

\frac{49}{16}

\frac{83}{8}

\frac{45}{4}

Câu 140: 1 điểm

Cho tứ diện ABCD có $\hat{D A B} = \hat{C B D} = 90^{\circ}$ ; AB=a; $A C = a \sqrt{5}$ ; $\hat{A B C} = 135^{\circ}$ . Biết góc giữa hai mặt phẳng (ABD), (BCD) bằng $30^{\circ}$ . Thể tích của tứ diện ABCD bằng

\frac{a^{3}}{2 \sqrt{3}}

\frac{a^{3}}{\sqrt{2}}

\frac{a^{3}}{3 \sqrt{2}}

\frac{a^{3}}{6}

Câu 141: 1 điểm

Cho tứ diện ABCD có

A B = C D = 4; A C = B D = 5;

AD = BC = 6. Thể tích của khối tứ diện ABCD là

\frac{15 \sqrt{6}}{4}

\frac{15 \sqrt{6}}{2}

\frac{45 \sqrt{6}}{4}

\frac{45 \sqrt{6}}{2}

Câu 142: 1 điểm

Một con kiến đang ở vị trí M là trung điểm cạnh A'D' của một chiếc hộp hình lập phương ABCD.A'B'C'D' cạnh 5cm. Con kiến muốn bò qua sáu mặt của chiếc hộp rồi quay trở lại M. Quãng đường bò đi ngắn nhất của con kiến là

16 \sqrt{2} c m

15 \sqrt{2} c m

12 \sqrt{2} c m

13 \sqrt{2} c m

Câu 143: 1 điểm

Cho hình chóp tứ giác đều SABCD một con kiến bò từ đỉnh A của đáy để đi tất cả các mặt xung quanh rồi trở về vị trí A. Biết cạnh bên bằng 6cm, cạnh đáy bằng 4cm. Quãng đường ngắn nhất mà con kiến đi là

13,48 c m

10,25 c m

12,05 c m

11,73 c m

Câu 144: 1 điểm

Cho hình chóp tứ giác đều SABCD có SA = a và $\hat{S A B} = \frac{11 π}{24}$ . Gọi Q là trung điểm cạnh SA. Trên các cạnh SB,SC,SD lần lượt lấy các điểm M,N,P không trùng với các đỉnh của hình chóp. Giá trị nhỏ nhất của tổng $A M + M N + N P + P Q$ theo a là

\frac{a \sqrt{2} \sin \frac{11 π}{24}}{3}

\frac{a \sqrt{3}}{2}

\frac{a \sqrt{2}}{4}

\frac{a \sqrt{3} \sin \frac{11 π}{12}}{3}

Câu 145: 1 điểm

Cho hình chóp đều SABC có $\hat{A S B} = 30^{0}, S A = 1$ . Lấy B',C' lần lượt thuộc cạnh SB,SC sao cho chu vi tam giác AB'C' nhỏ nhất. Tỉ số $\frac{V_{S . A B^{'} C^{'}}}{V_{S . A B C}}$ gần giá trị nào nhất trong các giá trị sau?

0,55

0,65

0,45

0,75

Câu 146: 1 điểm

Cho hình vẽ bên với E, F lần lượt là trung điểm các cạnh bên SB và SC. Khối chóp S.AEF có thể tích là

\frac{1}{24} a b c

\frac{1}{12} a b c

\frac{1}{8} a b c

\frac{11}{12} a b c

Câu 147: 1 điểm

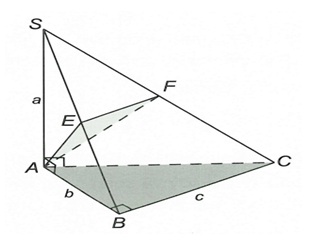
Cho hình chóp S.ABC có tam giác ABC vuông cân ở B, AC = $a \sqrt{2}$ , SA vuông góc với đáy ABC, SA = a. Gọi G là trọng tâm tam giác SBC, mặt phẳng $(α)$ qua AG và song song với BC cắt SC, SB lần lượt tại M, N. Thể tích của khối chóp S.AMN là

\frac{2 a^{3}}{27}

\frac{2 a^{3}}{9}

\frac{a^{3}}{6}

\frac{\sqrt{5} a^{3}}{3}

Câu 148: 1 điểm

Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau AB = a; AC = 2a và AD = 3a. Gọi M và N lần lượt là trung điểm của BD, CD. Thể tích của tứ diện ADMN là

V = a^{3}

V = \frac{2 a^{3}}{3}

V = \frac{3 a^{3}}{4}

V = \frac{a^{3}}{4}

Câu 149: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA vuông góc với mặt phẳng (ABC), AB = a, BC = $a \sqrt{3}$ , SA = a. Một mặt phẳng $(α)$ qua A vuông góc SC tại H và cắt SB tại K. Thể tích khối chóp S.AHK là

V_{S . A H K} = \frac{a^{3} \sqrt{3}}{20}

V_{S . A H K} = \frac{a^{3} \sqrt{3}}{30}

V_{S . A H K} = \frac{a^{3} \sqrt{3}}{60}

V_{S . A H K} = \frac{a^{3} \sqrt{3}}{90}

Câu 150: 1 điểm

Cho tứ diện ABCD có DA =1, DA $⊥$ (ABC). $Δ$ ABC là tam giác đều, có cạnh bằng 1. Trên ba cạnh DA, DB, DC lần lượt lấy ba điểm M, N, P mà $\frac{D M}{D A} = \frac{1}{2}, \frac{D N}{D B} = \frac{1}{3}, \frac{D P}{D C} = \frac{3}{4}$ . Thể tích của tứ diện MNPD là

V = \frac{\sqrt{3}}{12}

V = \frac{\sqrt{2}}{12}

V = \frac{\sqrt{3}}{96}

V = \frac{\sqrt{2}}{96}

Câu 151: 1 điểm

Cho hình chóp đều S.ABCD. Mặt phẳng (P) chứa AB và đi qua trọng tâm G của tam giác SAC cắt SC, SD lần lượt tại M, N. Tỉ số $\frac{V_{S . A B M N}}{V_{S . A B C D}}$ có giá trị là

\frac{1}{2}

\frac{3}{8}

\frac{1}{4}

\frac{3}{4}

Câu 152: 1 điểm

Cho hình chóp S.ABC, đáy ABC là tam giác vuông tại B có AB = a, BC = $a \sqrt{3}$ , SA vuông góc với mặt phẳng (ABC) và SA = 2a. Gọi H, K lần lượt là hình chiếu vuông góc của A trên các cạnh SB và SC. Thể tích của khối chóp A.BCKH là V. Tỉ số $\frac{a^{3}}{V}$ gần nào nhất giá trị nào trong các giá trị sau?

Câu 153: 1 điểm

Cho hình chóp tam giác S.ABC có M là trung điểm của SB, N là điểm trên cạnh SC sao cho NS=2NC, P là điểm trên cạnh SA sao cho PA=2PS. Kí hiệu $V_{1}, V_{2}$ lần lượt là thể tích của các khối tứ diện BMNP và SABC. Tính tỉ số $\frac{V_{1}}{V_{2}}$ .

\frac{V_{1}}{V_{2}} = \frac{1}{9}

\frac{V_{1}}{V_{2}} = \frac{3}{4}

\frac{V_{1}}{V_{2}} = \frac{2}{3}

\frac{V_{1}}{V_{2}} = \frac{1}{3}

Câu 154: 1 điểm

Cho tứ diện S.ABC, M và N là các điểm lần lượt thuộc SA và SB sao cho MA=2SM, SN=2NB, $(α)$ là mặt phẳng qua MN và song song với SC. Kí hiệu $(H_{1})$ và $(H_{2})$ là các khối đa diện có được khi chia khối tứ diện S.ABC bởi mặt phẳng $(α)$ , trong đó $(H_{1})$ chứa điểm S, $(H_{2})$ chứa điểm A; $V_{1}$ và $V_{2}$ lần lượt là thể tích của $(H_{1})$ và $(H_{2})$ . Tỉ số $\frac{V_{1}}{V_{2}}$ bằng

\frac{4}{5}

\frac{5}{4}

\frac{3}{4}

\frac{4}{3}

Câu 155: 1 điểm

Hình chóp S.ABC có M, N, P theo thứ tự là trung điểm SA, SB, SC. Giá trị $\frac{V_{M N P A B C}}{V_{S . A B C}}$ là

\frac{8}{7}

\frac{7}{8}

\frac{1}{8}

Câu 156: 1 điểm

Cho hình chóp S.ABC có tam giác ABC đều cạnh 2a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = $a \sqrt{3}$ . Gọi M, N lần lượt là trung điểm của AB và AC. Thể tích khối chóp S.AMN là

\frac{a^{3}}{2}

\frac{a^{3}}{4}

\frac{a^{3}}{6}

\frac{a^{3}}{3}

Câu 157: 1 điểm

Cho hình chóp S.ABC, trên các cạnh AB, BC, SC lần lượt lấy các điểm M, N, P sao cho AM=2MB, BN=4NC, SP=PC. Tỉ lệ thể tích hai khối chóp S.BMN và A.CPN là

\frac{4}{3}

\frac{8}{3}

\frac{5}{6}

Câu 158: 1 điểm

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Gọi G là trọng tâm tam giác ABC, góc giữa SG và mặt phẳng (SBC) là $30^{\circ}$ . Mặt phẳng (P) chứa BC và vuông góc với SA chia khối chóp S.ABC thành hai phần. Tỉ số thể tích hai phần là

\frac{1}{6}

\frac{1}{7}

\frac{6}{7}

\frac{2}{3}

Câu 159: 1 điểm

Cho hình chóp S.ABC có SA=2cm, SB=3cm, SC=4cm, $\hat{A S B} = 60^{0}, \hat{B S C} = 90^{0}$ $, \hat{A S C} = 120^{0}$ . Thể tích của khối chóp S.ABC là

2 \sqrt{2}

3 \sqrt{2}

2 \sqrt{3}

3 \sqrt{3}

Câu 160: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết $V_{S . A E F} = \frac{1}{4} V_{S . A B C}$ . Thể tích V của khối chóp S.ABC là

\frac{a^{3}}{4}

\frac{a^{3}}{12}

\frac{a^{3}}{2}

\frac{a^{3}}{8}

Câu 161: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hai mặt bên (SAB), (SAD) cùng vuông góc với mặt đáy. Gọi $V_{1}, V_{2}$ lần lượt là thể tích khối chóp S.AHK và S.ACD với H, K lần lượt là trung điểm SC, SD. Tính độ dài đường cao h của khối chóp S.ABCD và tỉ số $k = \frac{V_{1}}{V_{2}}$ .

h = a; k = \frac{1}{4}

h = a; k = \frac{1}{6}

h = 2 a; k = \frac{1}{8}

h = 2 a; k = \frac{1}{3}

Câu 162: 1 điểm

Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông cạnh bằng 20cm, cạnh SA=30cm và vuông góc với đáy. Gọi B’, D’ lần lượt là hình chiếu vuông góc của A lên SB và SD. Mặt phẳng (AB’D’) cắt SC tại C’. Thể tích khối chóp S.AB’C’D’ gần nhất giá trị nào dưới đây?

2120 c m^{3}

2770 c m^{3}

1440 c m^{3}

1470 c m^{3}

Câu 163: 1 điểm

Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A’ trên cạnh SA sao cho $S A' = \frac{1}{3} S A$ . Mặt phẳng qua A’ và song song với đáy của hình chóp cắt các cạnh SB, SC, SD lần lượt tại B’, C’, D’. Khi đó thể tích chóp S.A’B’C’D’ bằng

\frac{V}{3}

\frac{V}{9}

\frac{V}{27}

\frac{V}{81}

Câu 164: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Gọi H và K lần lượt là trung điểm của SB, SD. Tỉ số thể tích $\frac{V_{S . A B C D}}{V_{A O H K}}$ bằng

Câu 165: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, $\hat{B A D} = 60^{0}$ . Gọi H là trung điểm của OB và SH vuông góc với (ABCD). Góc giữa SC và (ABCD) bằng $45^{\circ}$ . Thể tích của khối chóp S.AHCD là

\frac{\sqrt{35}}{32} a^{3}

\frac{\sqrt{39}}{24} a^{3}

\frac{\sqrt{35}}{24} a^{3}

\frac{\sqrt{39}}{32} a^{3}

Câu 166: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Gọi M, N, P lần lượt là trung điểm SB, BC, CD. Thể tích của CMNP theo a bằng

\frac{a^{3} \sqrt{3}}{16}

\frac{a^{3} \sqrt{3}}{32}

\frac{a^{3} \sqrt{3}}{96}

\frac{a^{3} \sqrt{3}}{48}

Câu 167: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a, AD= $a \sqrt{3}$ , SA=2a và SA vuông góc với mặt đáy. Một mặt phẳng đi qua A và vuông góc với SC, cắt SB, SC, SD lần lượt tại H, I, K. Thể tích khối chóp S.AHIK là

\frac{8 a^{3} \sqrt{3}}{35}

\frac{34 a^{3} \sqrt{3}}{105}

\frac{2 a^{3} \sqrt{3}}{7}

\frac{2 a^{3} \sqrt{3}}{21}

Câu 168: 1 điểm

Cho hình chóp tứ giác đều S.ABCD có AB = a, SA= $a \sqrt{2}$ . Gọi M là trung điểm của SC, (P) là mặt phẳng qua AM song song với BD cắt SB, SD lần lượt tại E, F. Thể tích khối chóp S.AEMF là

\frac{a^{3} \sqrt{6}}{18}

\frac{a^{3} \sqrt{6}}{6}

\frac{a^{3} \sqrt{6}}{3}

a^{3} \sqrt{6}

Câu 169: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình thang, $\hat{B A D} = \hat{A B C =} 90^{0}$ , AB = BC = a, AD = 2a, SA vuông góc với đáy và SA = 2a. Gọi M, N lần lượt là trung điểm của SA và SD. Thể tích khối chóp S.BCNM bằng

\frac{a^{3}}{6}

\frac{a^{3}}{3}

\frac{a^{3}}{2}

\frac{a^{3}}{4}

Câu 170: 1 điểm

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc $60^{\circ}$ . Gọi M là điểm đối xứng của C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng

\frac{7}{5}

\frac{1}{7}

\frac{7}{3}

\frac{6}{5}

Câu 171: 1 điểm

Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB=a, AD=b. Cạnh SA=2a của hình chóp vuông góc với đáy. Gọi M là một điểm nằm trên cạnh SA sao cho AM=x $(0 < x < 2 a)$ . Tìm x để mặt phẳng (MBC) chia khối chóp trên ra hai phần có thể tích bằng nhau.

x = a (4 - \sqrt{5})

x = a (3 - \sqrt{5})

x = a (3 - \sqrt{2})

x = 2 a (3 - \sqrt{5})

Câu 172: 1 điểm

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N và P lần lượt là trung điểm của các đoạn BC, CD và SA. Mặt phẳng (MNP) chia khối chóp thành hai phần có thể tích lần lượt là $V_{1}$ và $V_{2}$ . Biết rằng $V_{1} \leq V_{2}$ , tỉ số $\frac{V_{1}}{V_{2}}$ bằng

\frac{1}{2}

\frac{5}{6}

\frac{2}{3}

Câu 173: 1 điểm

Cho hình tứ diện đều ABCD có cạnh bằng 3. Gọi $G_{1}, G_{2}, G_{3}, G_{4}$ lần lượt là trọng tâm của bốn mặt của tứ diện ABCD. Tính thể tích V của khối tứ diện $G_{1} G_{2} G_{3} G_{4}$ .

V = \frac{\sqrt{2}}{4}

V = \frac{\sqrt{2}}{18}

V = \frac{9 \sqrt{2}}{32}

V = \frac{\sqrt{2}}{12}

Câu 174: 1 điểm

Cho khối tứ diện có thể tích V. Gọi V’ là thể tích khối đa diện có các đỉnh là trung điểm các cạnh của khối tứ diện đã cho. Tính tỉ số $\frac{V'}{V}$ .

\frac{V'}{V} = \frac{2}{3}

\frac{V'}{V} = \frac{1}{4}

\frac{V'}{V} = \frac{5}{8}

\frac{V'}{V} = \frac{1}{2}

Câu 175: 1 điểm

Cho khối chóp S.ABCD, trong đó ABCD là hình thang có các cạnh đáy AB, CD sao cho CD=4.AB, một mặt phẳng qua CD cắt SA, SB lần lượt tại các điểm M, N. Đặt $\frac{S M}{S A} = x,0 < x < 1$ . Tìm x sao cho thiết diện MNCD chia khối chóp đã cho thành hai phần có thể tích bằng nhau.

x = \frac{- 3 + \sqrt{13}}{2}

x = \frac{- 3 + \sqrt{17}}{2}

x = \frac{- 3 + \sqrt{15}}{2}

x = \frac{- 3 + \sqrt{19}}{2}

Câu 176: 1 điểm

Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V. Gọi M là trung điểm cạnh BB’, điểm N thuộc cạnh CC’ sao cho CN=2C’N. Tính thể tích khối chóp A.BCNM theo V.

V_{A . B C N M} = \frac{7 V}{12}

V_{A . B C N M} = \frac{7 V}{18}

V_{A . B C N M} = \frac{5 V}{18}

V_{A . B C N M} = \frac{V}{3}

Câu 177: 1 điểm

Cho lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB và B’C’. Mặt phẳng (A’NM) cắt cạnh BC tại P. Thể tích khối đa diện MBP.A’B’N bằng

\frac{7 a^{3} \sqrt{3}}{32}

\frac{a^{3} \sqrt{3}}{32}

\frac{7 a^{3} \sqrt{3}}{68}

\frac{7 a^{3} \sqrt{3}}{96}

Câu 178: 1 điểm

Cho lăng trụ ABC.A’B’C’ có thể tích bằng V. Trên các cạnh AA’, BB’ lần lượt lấy các điểm E, F sao cho AA’ = kA’E, BB’ = kB’F. Mặt phẳng (C’EF) chia khối trụ đã cho thành hai khối đa diện bao gồm khối chóp C’.A’B’FE có thể tích $V_{1}$ và khối đa diện ABCEFC’ có thể tích $V_{2}$ .Biết rằng $\frac{V_{1}}{V_{2}} = \frac{2}{7}$ . Giá trị k là

k = 4.

k = 3.

k = 1.

k = 2.

Câu 179: 1 điểm

Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng $60 c m^{3}$ , các điểm M, N, P lần lượt thuộc các cạnh AA’, BB’, CC’ sao cho AM = 2MA’, BN = 3NB’, CP = 4PC’. Thể tích của khối đa diện BC.MNP .

\frac{93}{2} c m^{3}

25 c m^{3}

31 c m^{3}

\frac{65}{3} c m^{3}

Câu 180: 1 điểm

Cho hình hộp ABCD.A’B’C’D’. Gọi $V_{1}, V_{2}$ lần lượt là thể tích khối tứ diện ACB’D’ và khối hộp ABCD.A’B’C’D’. Tỉ số $\frac{V_{1}}{V_{2}}$ bằng

\frac{1}{3}

\frac{1}{6}

\frac{1}{2}

\frac{1}{4}

Câu 181: 1 điểm

Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng $48 c m^{3}$ . Gọi M, N, P theo thứ tự là trung điểm các cạnh CC’, BC và B’C’. Tính thể tích của khối chóp A’.MNP.

8 c m^{3}

12 c m^{3}

24 c m^{3}

\frac{16}{3} c m^{3}

Câu 182: 1 điểm

Cho hình hộp ABCD.A’B’C’D’. Tỉ số thể tích của khối tứ diện A’C’BD và khối hộp ABCD.A’B’C’D’ bằng

\frac{1}{3}

\frac{1}{6}

\frac{1}{2}

\frac{1}{4}

Câu 183: 1 điểm

Một khúc gỗ có dạng với độ dài các cạnh được cho như hình vẽ bên.

Thể tích khối đa diện tương ứng là

V = 570.

V = 190.

V = 360.

V = 540.

Câu 184: 1 điểm

Một khúc gỗ có dạng với độ dài các cạnh được cho như hình vẽ bên. Thể tích khối đa diện tương ứng là

V = 24.

V = 96.

V = 126.

V = 102.

Câu 185: 1 điểm

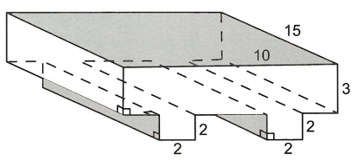
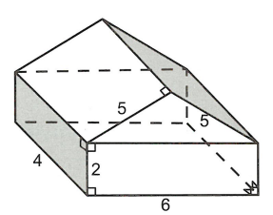
Một khúc gỗ có dạng với độ dài các cạnh được cho như hình vẽ bên dưới.Thể tích khối đa diện tương ứng là

V = \frac{40}{3}

V = 32.

V = 40.

V = 20.

Câu 186: 1 điểm

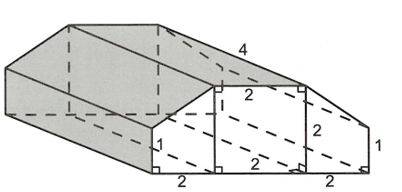
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau. Gọi $G_{1}, G_{2}, G_{3}$ và $G_{4}$ lần lượt là trọng tâm các mặt ABC, ABD, ACD và BCD. Biết AB = 6a, AC = 9a, AD = 12a. Tính theo a thể tích khối tứ diện $G_{1} G_{2} G_{3} G_{4}$ .

4 a^{3}

a^{3}

108 a^{3}

36 a^{3}

Câu 187: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA $⊥$ (ABCD). Trên đường thẳng vuông góc với (ABCD) tại D lấy điểm S’ thỏa mãn $S^{'} D = \frac{1}{2} S A$ và S’, S ở cùng phía đối với mặt phẳng (ABCD). Gọi $V_{1}$ là phần thể tích chung của hai khối chóp S.ABCD và S’.ABCD. Gọi $V_{2}$ là thể tích khối chóp S.ABCD. Tỉ số $\frac{V_{1}}{V_{2}}$ bằng

\frac{4}{9}

\frac{7}{9}

\frac{7}{18}

\frac{1}{3}

Câu 188: 1 điểm

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng cạnh bên bằng a. Gọi A’, B’, C’ lần lượt là trọng tâm của tam giác SBC, SCA và SAB. Tính thể tích khối ABC.A’B’C’

\frac{5 a^{3} \sqrt{2}}{108}

\frac{a^{3} \sqrt{2}}{27}

\frac{4 a^{3} \sqrt{2}}{81}

\frac{5 a^{3} \sqrt{2}}{96}

Câu 189: 1 điểm

Cho lăng trụ tam giác ABC.A’B’C’ có thể tích bằng V. Lấy M, N, P lần lượt là trung điểm các cạnh AB’, BC’, CA’. Thể tích khối đa diện MNPABC bằng

\frac{1}{2} V

\frac{2}{3} V

\frac{3}{4} V

\frac{3}{8} V

Câu 190: 1 điểm

Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a và góc giữa (AB’C’) và mặt phẳng (ABC) bằng $60^{\circ}$ . Mặt phẳng $(α)$ đi qua trọng tâm tứ diện AA’B’C’ và song song với mặt phẳng (AB’C’), lần lượt cắt các cạnh AA’, A’B’, A’C’ tại P, Q, R. Thể tích khối đa diện PQRB’C’CAB là

\frac{165 a^{3} \sqrt{3}}{512}

\frac{55 a^{3} \sqrt{3}}{512}

\frac{27 a^{3} \sqrt{3}}{64}

\frac{27 a^{3} \sqrt{3}}{512}

Câu 191: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành có thể tích là V. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC. Điểm I thuộc đoạn SA sao cho $\frac{I A}{I S} = \frac{2}{3}$ . Biết mặt phẳng (MNI) chia khối chóp S.ABCD thành hai phần. Khi đó thể tích của phần đa diện không chứa đỉnh S tính thông qua V được kết quả là

\frac{3}{4}

\frac{11}{20}

\frac{16}{21}

\frac{13}{20}

Câu 192: 1 điểm

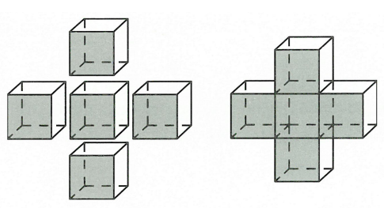
Người ta ghép 5 khối lập phương cạnh a để được khối hộp chữ thập như hình dưới. Tính diện tích toàn phần của khối hộp chữ thập đó.

S_{t p} = 20 a^{2}

S_{t p} = 12 a^{2}

S_{t p} = 30 a^{2}

S_{t p} = 22 a^{2}

Câu 193: 1 điểm

Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB=a, AD=b, SA vuông góc với đáy, SA=2a. Điểm M thuộc đoạn SA, AM=x. Giá trị của x để mặt phẳng (MBC) chia khối chóp S.ABCD thành hai khối có thể tích bằng nhau là

x = (2 + \sqrt{5}) a

x = (3 + \sqrt{5}) a

x = (2 - \sqrt{5}) a

x = (3 - \sqrt{5}) a

Câu 194: 1 điểm

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a, BC=b, AA’=c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng

\frac{1}{2}

\frac{1}{5}

\frac{1}{8}

\frac{1}{4}

Câu 195: 1 điểm

Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a, chiều cao 3a. Mặt phẳng (P) qua B’ và vuông góc với A’C chia lăng trụ thành hai khối. Biết thể tích của hai khối là $V_{1}$ và $V_{2}$ với $V_{1} < V_{2}$ . Tỉ số $\frac{V_{1}}{V_{2}}$ bằng

\frac{1}{47}

\frac{1}{107}

\frac{1}{7}

\frac{1}{108}

Câu 196: 1 điểm

Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A’C’, BB’. Thể tích của khối tứ diện CMNP bằng:

\frac{5}{24} V

\frac{1}{4} V

\frac{7}{24} V

\frac{1}{3} V

Câu 197: 1 điểm

Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB và B’C’. Mặt phẳng (A’MN) cắt cạnh BC tại P. Thể tích của khối đa diện MBP.A’B’N là

\frac{\sqrt{3} a^{3}}{24}

\frac{\sqrt{3} a^{3}}{12}

\frac{7 \sqrt{3} a^{3}}{96}

\frac{7 \sqrt{3} a^{3}}{32}

Câu 198: 1 điểm

Cho lăng trụ tam giác đều ABC.A’B’C’ cạnh đáy bằng a, chiều cao bằng 2a. Mặt phẳng (P) qua B’ và vuông góc với A’C chia lăng trụ thành hai khối. Biết thể tích của hai khối là $V_{1}$ và $V_{2}$ với $V_{1} < V_{2}$ . Tỉ số $\frac{V_{1}}{V_{2}}$ bằng

\frac{1}{47}

\frac{1}{23}

\frac{1}{11}

\frac{1}{7}

Câu 199: 1 điểm

Cho khối tứ diện đều ABCD cạnh bằng 2cm. Gọi M, N, P lần lượt là trọng tâm của ba tam giác ABC, ABD, ACD. Tính thể tích V của khối chóp AMNP.

V = \frac{\sqrt{2}}{162} c m^{3}

V = \frac{2 \sqrt{2}}{81} c m^{3}

V = \frac{4 \sqrt{2}}{81} c m^{3}

V = \frac{\sqrt{2}}{144} c m^{3}

Câu 200: 1 điểm

Cho hình lăng trụ ABC.A’B’C’. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AA’, BB’, CC’ sao cho AM=2MA’, NB’=2NB, PC=PC’. Gọi $V_{1}$ , $V_{2}$ lần lượt là thể tích của hai khối đa diện ABCMNP và A’B’C’MNP. Tính tỉ số $\frac{V_{1}}{V_{2}}$ .

\frac{V_{1}}{V_{2}} = 2

\frac{V_{1}}{V_{2}} = \frac{1}{2}

\frac{V_{1}}{V_{2}} = 1

\frac{V_{1}}{V_{2}} = \frac{2}{3}

Câu 201: 1 điểm

Cho tứ diện ABCD có AB=CD=11m, BC=AD=20m, BD=AC=21m. Thể tích khối chóp tứ diện ABCD bằng

360 m^{3}

720 m^{3}

770 m^{3}

340 m^{3}

Câu 202: 1 điểm

Cho hình chóp S.ABC có AB=a, AC= $a \sqrt{3}$ , SB>2a và $\hat{A B C} = \hat{B A S} = \hat{B C S} = 90^{\circ}$ . Biết sin của góc giữa đường thẳng SB và mặt phẳng (SAC) bằng $\frac{\sqrt{11}}{11}$ . Thể tích của khối chóp S.ABC bằng

\frac{2 a^{3} \sqrt{3}}{9}

\frac{a^{3} \sqrt{3}}{9}

\frac{a^{3} \sqrt{6}}{6}

\frac{a^{3} \sqrt{6}}{3}

Câu 203: 1 điểm

Cho tứ diện ABCD có tam giác ABD đều cạnh a, tam giác ABC vuông tại B, BC= $\sqrt{3}$ . Khoảng cách giữa hai đường thẳng AB và CD bằng $\frac{\sqrt{3}}{2}$ . Thể tích của khối tứ diện ABCD bằng

\frac{2}{3}

\frac{1}{2}

\frac{\sqrt{3}}{6}

\frac{\sqrt{3}}{2}

Câu 204: 1 điểm

Cho hình chóp S.ABC có đáy là tam giác cân tại A, AB=a, $\hat{B A C} = 120^{\circ}$ , $\hat{S B A} = \hat{S C A} = 90^{\circ}$ . Gọi $φ$ là góc giữa SB và (SAC) thỏa mãn $s i n φ = \frac{\sqrt{3}}{8}$ , khoảng cách từ S đến mặt đáy nhỏ hơn 2a. Thể tích của khối chóp S.ABC bằng

\frac{\sqrt{3} a^{3}}{4}

\frac{\sqrt{3} a^{3}}{6}

\frac{\sqrt{3} a^{3}}{12}

\frac{\sqrt{3} a^{3}}{24}

Câu 205: 1 điểm

Cho hai hình vuông ABCD và ABEF có cạnh bằng a và lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Lấy lần lượt hai điểm H, S sao cho: $\vec{D H} + 3 \vec{E H} = \vec{0}$ và $\vec{S H} + \vec{B H} = \vec{0}$ . Tính theo a thể tích khối đa diện ABCDSEF.

\frac{7}{6} a^{3}

\frac{1}{2} a^{3}

\frac{2}{3} a^{3}

\frac{5}{6} a^{3}

Câu 206: 1 điểm

Một cái hộp hình chữ nhật có kích thước ba cạnh lần lượt là 4cm, 6cm, 9cm như hình vẽ. Một con kiến ở vị trí A muốn đến vị trí B. Biết rằng con kiến chỉ có thể bò trên cạnh hay trên bề mặt của hình hộp đã cho. Gọi x cm là quãng đường ngắn nhất con kiến đi từ A đến B. Khẳng định nào sau đây đúng?

x \in (15; 16)

x \in (13; 14)

x \in (12; 13)

x \in (14; 15)

Câu 207: 1 điểm

Tứ diện SABC có các mặt SAB, SBC, SCA, có diện tích bằng nhau và $\hat{A S B} + \hat{A S C} + \hat{C S B} = 180^{\circ}$ . Biết rằng $S A = a = 4, S B = b = 5, S C = c = 6$ . Thể tích khối tứ diện SABC là

\frac{7 \sqrt{3}}{2}

\frac{15 \sqrt{3}}{2}

\frac{7 \sqrt{6}}{2}

\frac{15 \sqrt{6}}{2}

Câu 208: 1 điểm

Một khối hộp đựng giấy ăn hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao lần lượt là 25cm; 14cm; 8cm (như hình vẽ). Một con kiến xuất phát từ A muốn đến điểm B thì quãng đường đi ngắn nhất là bao nhiêu?

41,12cm.

39,82cm.

40,19cm.

38,12cm.

Câu 209: 1 điểm

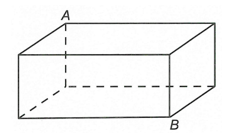
Cho tứ diện ABCD có $\hat{A C D} + \hat{B C D} = \hat{C A D} + \hat{B A D} + \hat{B A C} = \hat{C B D} + \hat{A B D} + \hat{A B C} = 180^{\circ}$ , $\hat{A C B} = 60^{\circ}$ . Biết chu vi tam giác ABC bằng 3. Giá trị lớn nhất của diện tích toàn phần của tứ diện ABCD bằng

\frac{4 \sqrt{3}}{3}

\frac{2 \sqrt{3}}{3}

\frac{4}{3}

\frac{5 \sqrt{3}}{3}

Câu 210: 1 điểm

Cho hình chóp SABC có đáy là tam giác ABC vuông cân tại C và SA vuông góc với mặt phẳng đáy. Cho SC = a, mặt phẳng (SBC) tạo với mặt đáy một góc $α$ . Thể tích khối chóp SABC đạt giá trị lớn nhất là

\frac{a^{3}}{16}

\frac{a^{3} \sqrt{3}}{27}

\frac{a^{3} \sqrt{3}}{48}

\frac{a^{3} \sqrt{2}}{24}

Câu 211: 1 điểm

Cho hình chóp SABC có SA là đoạn thẳng thay đổi sao cho $x \in (0; \sqrt{3})$ , $S A = x$ , các cạnh còn lại đều bằng 1. Thể tích khối chóp SABC đạt giá trị lớn nhất là

\frac{1}{4}

\frac{1}{16}

\frac{1}{12}

\frac{1}{8}

Câu 212: 1 điểm

Cho hình chóp SABCDcó đáy ABCDlà hình vuông cạnh 2a. Tam giác SABvuông tại Svà nằm trong mặt phẳng vuông góc với đáy. Gọi $α$ là góc tạo bởi đường thẳng SD và mặt phẳng (SBC), với $α < 45 °$ . Tìm giá trị lớn nhất của thể tích khối chóp SABCD

4 a^{3}

\frac{8 a^{3}}{\begin{array}{l} 3 \end{array}}

\frac{4 a^{3}}{\begin{array}{l} 3 \end{array}}

\frac{2 a^{3}}{\begin{array}{l} 3 \end{array}}

Câu 213: 1 điểm

Khối chóp SABCD có đáy là hình thoi cạnh a, $S A = S B = S C = a,$ cạnh SD thay đổi. Thể tích lớn nhất của khối chóp SABCD là

\frac{a^{3}}{2}

\frac{a^{3}}{8}

\frac{3 a^{3}}{8}

\frac{a^{3}}{4}

Câu 214: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh 2a. Tam giác SABvuông tại Svà nằm trong mặt phẳng vuông góc với đáy. Gọi $α$ là góc tạo bởi đường thẳng SD và mặt phẳng (SBC), với $α < 45 °$ . Tìm giá trị lớn nhất của thể tích khối chóp SABCD

4 a^{3}

\frac{8 a^{3}}{\begin{array}{l} 3 \end{array}}

\frac{4 a^{3}}{\begin{array}{l} 3 \end{array}}

\frac{2 a^{3}}{\begin{array}{l} 3 \end{array}}

Câu 215: 1 điểm

Khối chóp SABCD có đáy là hình thoi cạnh a, $S A = S B = S C = a,$ cạnh SD thay đổi. Thể tích lớn nhất của khối chóp SABCD là

\frac{a^{3}}{2}

\frac{a^{3}}{8}

\frac{3 a^{3}}{8}

\frac{a^{3}}{4}

Câu 216: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh bằng 2, SA = 2 và SA vuông góc với mặt phẳng đáy (ABCD). Gọi M,N là hai điểm thay đổi trên hai cạnh AB,AD sao cho mặt phẳng (SMC) vuông góc với mặt phẳng (SNC). Tính tổng $T = \frac{1}{A N^{2}} + \frac{1}{A M^{2}}$ khi thể tích khối chóp $S . A M C N$ đạt giá trị lớn nhất.

T = 2.

T = \frac{5}{4} .

T = \frac{2 + \sqrt{3}}{4} .

T = \frac{13}{9} .

Câu 217: 1 điểm

Cho hình chóp SABC có đáy là tam giác vuông tại A với $A B = 1, A C = \sqrt{3} .$ Hình chiếu của S trên mặt phẳng đáy là điểm H sao cho các mặt phẳng (SAB) và (SAC) cùng tạo với SH góc $30 °$ và mặt phẳng (SBC) tạo với mặt phẳng đáy một góc $60 °$ . Thể tích lớn nhất của khối chóp SABC là

V_{\max} = \frac{1 + \sqrt{3}}{4} .

V_{\max} = \frac{3 - \sqrt{3}}{4} .

V_{\max} = \frac{\sqrt{3} - 1}{4} .

V_{\max} = \frac{3 + \sqrt{3}}{4} .

Câu 218: 1 điểm

Cho hình chóp tứ giác đều SABCD có các cạnh bên bằng a, góc tạo bởi mặt bên và mặt phẳng đáy là $α$ với $α \in (0; \frac{π}{2})$ . Thể tích khối chóp SABCD đạt giá trị lớn nhất là

\frac{4 a^{3} \sqrt{7}}{49} .

\frac{4 a^{3} \sqrt{3}}{27} .

\frac{2 a^{3} \sqrt{3}}{9} .

\frac{4 a^{3} \sqrt{15}}{75} .

Câu 219: 1 điểm

Một hình hộp chữ nhật có diện tích toàn phần là S. Thể tích lớn nhất của khối hộp chữ nhật là

\frac{S \sqrt{S}}{3} .

\frac{S \sqrt{S}}{36} .

\frac{S \sqrt{6 S}}{36} .

\frac{S \sqrt{3 S}}{9} .

Câu 220: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C', đáy ABC là tam giác vuông tại A. Khoảng cách từ AA' đến $(B C C^{'} B^{'})$ và khoảng cách từ C đến (ABC') đều bằng x không đổi, góc giữa hai mặt phẳng (ABC') và (ABC) bằng $α \in (0; \frac{π}{2})$ . Để thể tích khối lăng trụ $A B C . A^{'} B^{'} C^{'}$ nhỏ nhất thì góc $α$ có giá trị gần nhất giá trị nào sau đây?

25 °

35 °

45 °

55 °

Câu 221: 1 điểm

Cho hình hộp chữ nhật ABCD.A'B'C'D' có $A B < B C$ và BD = 3cm. Hai mặt phẳng $(A C C^{'} A^{'})$ và $(B D D^{'} B^{'})$ hợp với nhau một góc $α (0 < α \leq \frac{π}{2})$ . Đường chéo B'D hợp với mặt phẳng $(C D D^{'} C^{'})$ một góc $β (0 < β < \frac{π}{2})$ . Hai góc $α, β$ thay đổi nhưng thỏa mãn hình hộp $A D D^{'} A^{'} . B C C^{'} B^{'}$ luôn là hình lăng trụ đều. Giá trị lớn nhất thể tích của khối hộp $A B C D . A^{'} B^{'} C^{'} D^{'}$

\sqrt{3} c m^{3}

2 \sqrt{3}

c m^{3}

6 \sqrt{3} c m^{3}

12 \sqrt{3}

c m^{3}

Câu 222: 1 điểm

Cho hình chóp SABC có $S A = a, S B = 2 a, S C = 3 a$ . Giá trị lớn nhất của thể tích khối chóp SABC là

3 \sqrt{2} a^{3}

2 a^{3}

a^{3}

\frac{4}{3} a^{3}

Câu 223: 1 điểm

Cho hình chóp SABCD có SA thay đổi và tất cả các cạnh còn lại có độ dài bằng a. Khối chóp SABCD có thể tích lớn nhất khi SA đạt giá trị nào dưới đây?

S A = a \sqrt{2} .

S A = a .

S A = \frac{a \sqrt{6}}{2} .

S A = \frac{a \sqrt{3}}{2} .

Câu 224: 1 điểm

Trên 3 tia $O x, O y, O z$ vuông góc với nhau từng đôi, lấy lần lượt các điểm A,B,C sao cho $O A = a; O B = b; O C = c .$ Giả sử A cố định còn B,C thay đổi nhưng luôn luôn thỏa mãn $O A = O B + O C .$ Thể tích khối tứ diện OABC đạt giá trị lớn nhất là

\frac{a^{3}}{6} .

\frac{a^{3}}{8} .

\frac{a^{3}}{24} .

\frac{a^{3}}{32} .

Câu 225: 1 điểm

Cho hình chóp SABC có độ dài các cạnh $S A = B C = x, S B = A C = y, S C = A B = z$ thỏa mãn $x^{2} + y^{2} + z^{2} = 9$ . Giá trị lớn nhất của thể tích khối chóp SABC là

\frac{3 \sqrt{6}}{8} .

\frac{3 \sqrt{6}}{4} .

\frac{2 \sqrt{6}}{5} .

\frac{\sqrt{6}}{4} .

Câu 226: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA = y và vuông góc với đáy (ABCD). Trên cạnh AD lấy điểm M và đặt $A M = x,$ biết $x^{2} + y^{2} = a^{2}$ . Thể tích lớn nhất của khối chóp SABCM là

\frac{a^{3} \sqrt{3}}{3} .

a^{3} \sqrt{3} .

\frac{a^{3} \sqrt{3}}{8} .

\frac{a^{3} \sqrt{3}}{24} .

Câu 227: 1 điểm

Cho tứ diện SABC, có SA,AB,AC đôi một vuông góc với nhau, độ dài các cạnh $B C = a, S B = b, S C = c .$ Thể tích khối tứ diện SABC đạt giá trị lớn nhất là

\frac{a b c \sqrt{2}}{4} .

\frac{a b c \sqrt{2}}{8} .

\frac{a b c \sqrt{2}}{12} .

\frac{a b c \sqrt{2}}{24} .

Câu 228: 1 điểm

Cho hình chóp SABCD có ABCD là hình thoi cạnh $a, S A = S B = S C = a$ . Thể tích lớn nhất của khối chóp SABCD là

\frac{3 a^{3}}{8} .

\frac{a^{3}}{2} .

\frac{a^{3}}{8} .

\frac{a^{3}}{4} .

Câu 229: 1 điểm

Xét khối tứ diện ABCD có cạnh AB = x, các cạnh còn lại đều bằng $2 \sqrt{3}$ . Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất.

x = \sqrt{6} .

x = \sqrt{14} .

x = 3 \sqrt{2} .

x = 2 \sqrt{3} .

Câu 230: 1 điểm

Cho khối hộp chữ nhật có thể tích bằng 64. Tổng độ dài ba cạnh xuất phát từ cùng một đỉnh đạt giá trị nhỏ nhất là

Câu 231: 1 điểm

Cho tứ diện ABCD, có AB = CD = 6, khoảng cách giữa AB và CD là 8, góc giữa AB và CD là $α$ . Thể tích khối tứ diện ABCD đạt giá trị lớn nhất là

Câu 232: 1 điểm

Cho khối chóp SABC có đáy là tam giác vuông cân tại B. Khoảng cách từ A đến mặt phẳng (SBC) bằng $a \sqrt{2}$ , $\hat{S A B} = \hat{S C B} = 90 °$ . Độ dài cạnh AB để khối chóp SABC có thể tích nhỏ nhất là

A B = 3 a \sqrt{5} .

A B = a \sqrt{3} .

A B = 2 a .

A B = \frac{a \sqrt{10}}{2} .

Câu 233: 1 điểm

Khối chóp SABCD có đáy là hình thoi cạnh $a, S A = S B = S C = a,$ cạnh SD thay đổi. Thể tích lớn nhất của khối chóp SABCD là

\frac{a^{3}}{2} .

\frac{a^{3}}{8} .

\frac{3 a^{3}}{8} .

\frac{a^{3}}{4} .

Câu 234: 1 điểm

Trong tất cả các hình chóp tứ giác đều có $d = \sqrt{3}$ là khoảng cách giữa hai đường thẳng chéo nhau gồm một đường thẳng chứa một đường chéo của đáy và đường thẳng còn lại chứa một cạnh bên hình chóp. Thể tích nhỏ nhất của khối chóp là

9 \sqrt{3} .

27.

Câu 235: 1 điểm

Cho x,y là các số thực dương. Xét các hình chóp SABC có $S A = x, B C = y,$ các cạnh còn lại đều bằng 1. Khi x,y thay đổi, thể tích khối chóp SABC có giá trị lớn nhất là

\frac{2 \sqrt{3}}{27} .

\frac{1}{8} .

\frac{\sqrt{3}}{8} .

\frac{\sqrt{2}}{12} .

Câu 236: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình thoi tâm O, cạnh bằng 1; SO vuông góc với mặt phẳng đáy (ABCD) và SC = 1. Thể tích lớn nhất của khối chóp SABCD là

\frac{2 \sqrt{3}}{9} .

\frac{2 \sqrt{3}}{3} .

\frac{2 \sqrt{3}}{27} .

\frac{4 \sqrt{3}}{27} .

Câu 237: 1 điểm

Trên đường thẳng A và vuông góc với mặt phẳng chứa tam giác đều ABC cạnh bằng 2, lấy các điểm M và N không trùng với A sao cho (MBC) vuông góc với (NBC). Giá trị nhỏ nhất thể tích tứ diện BMNC là

2 \sqrt{3}

2 \sqrt{2}

Câu 238: 1 điểm

Cho khối chóp tứ giác đều SABCD mà khoảng cách từ đỉnh A đến (SBC) bằng 2a. Với giá trị nào của góc giữa mặt bên và cho hình chóp SABCD có đáy ABCD là hình vuông cạnh $a, S A = a \sqrt{2}$ và vuông góc với mặt đáy (ABCD). Gọi M là điểm di động trên cạnh CD và H là hình chiếu vuông góc của S lên đường thẳng BM. Khi điểm M di động trên cạnh CD, thể tích khối chóp SABH có giá trị lớn nhất bằng

\frac{a^{3} \sqrt{2}}{6} .

\frac{a^{3} \sqrt{2}}{8} .

\frac{a^{3} \sqrt{2}}{12} .

\frac{a^{3} \sqrt{2}}{15} .

Câu 239: 1 điểm

Cho lăng trụ đều ABC.A'B'C' có tát cả các cạnh bằng nhau và bằng a. Lấy các điểm M,N nằm trên cạnh BC, gọi P,Q lần lượt nằm trên cạnh AC,AB sao cho MNPQ là hình chữ nhật. Hình hộp chữ nhật $M N P Q . M^{'} N^{'} P^{'} Q^{'}$ nội tiếp trong lăng trụ đều ABC.A'B'C' có thể tích lớn nhất là

\frac{a^{3} \sqrt{3}}{4}

\frac{a^{3}}{8}

\frac{a^{3} \sqrt{3}}{8}

\frac{a^{3} \sqrt{6}}{4}

Câu 240: 1 điểm

Cho tứ diện ABCD có tam giác ABC vuông tại $A, A B = 3 a, A C = a .$ Mặt phẳng $(D B C), (D A C), (D A B)$ lần lượt tạo với mặt phẳng (ABC) các góc $90 °, α, β$ trong đó $x + y + z$ . Thể tích khối tứ diện ABCD có giá trị lớn nhất là

\frac{a^{3} \sqrt{3}}{4} .

\frac{3 a^{3}}{13} .

\frac{3 a^{3} \sqrt{2}}{10} .

\frac{3 a^{3}}{8} .

Câu 241: 1 điểm

Cho khối chóp tứ giác đều SABCD mà khoảng cách từ đỉnh A đến (SBC) bằng 2a. Với giá trị nào của góc giữa mặt bên và mặt đáy của khối chóp thì thể tích khối chóp nhỏ nhất ?

\cos α = \frac{1}{\sqrt{3}} .

\cos α = \frac{\sqrt{2}}{\sqrt{3}} .

\cos α = \frac{1}{2} .

\cos α = \frac{\sqrt{3}}{2} .

Câu 242: 1 điểm

Cho hình chóp SABCD có đáy là hình vuông cạnh AB = 1, cạnh bên $S A = 1, S A ⊥ (A B C D) .$ Gọi M là điểm di động trên đoạn CD và N là điểm di động trên đoạn CB sao cho $\hat{M A N} = 60 °$ . Thể tích nhỏ nhất của khối chóp SAMN là

\frac{2 - \sqrt{3}}{3} .

\frac{2 + \sqrt{3}}{9} .

\frac{2 \sqrt{3} - 3}{3} .

\frac{2 \sqrt{3} - 3}{9} .

Câu 243: 1 điểm

Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD nội tiếp đường tròn đường kính $B D = a \sqrt{3}, \hat{A B D} = α, \hat{C B D} = β$ , tam giác A'AC đều. Hình chiếu vuông góc của A' trên (ABCD) là trung điểm H của AC. Thể tích khối lăng trụ ABCD.A'B'C'D' đạt giá trị lớn nhất là

\frac{3 a^{3}}{4}

\frac{a^{3} \sqrt{3}}{12}

\frac{9 a^{3}}{4}

\frac{a^{3} \sqrt{3}}{4}

Câu 244: 1 điểm

Cho khối chóp SABC có $S A = S B = S C = a, \hat{A S B} = 60 °, \hat{B S C} = 90 °, \hat{C S A} = 120 ° .$ Gọi M,N lần lượt là điểm trên cạnh AB và SC sao cho $\frac{C N}{S C} = \frac{A M}{A B}$ . Khi độ dài đoạn MN đạt giá trị nhỏ nhất thì thể tích của khối chóp SAMN là

V = \frac{a^{3} \sqrt{2}}{72} .

V = \frac{5 a^{3} \sqrt{2}}{72} .

V = \frac{5 a^{3} \sqrt{2}}{432} .

V = \frac{a^{3} \sqrt{2}}{432} .

Câu 245: 1 điểm

Cho hình vuông ABCD cạnh a, trên đường thẳng vuông góc với (ABCD) tại A ta lấy điểm S di động. Hình chiếu vuông góc của A lên SB,SD lần lượt là H,K. Thể tích lớn nhất của tứ diện ACHK bằng

\frac{a^{3}}{6} .

\frac{a^{3} \sqrt{3}}{16} .

\frac{a^{3} \sqrt{3}}{12} .

\frac{a^{3} \sqrt{6}}{32} .

Câu 246: 1 điểm

Cho hình hộp chữ nhật có tổng diện tích các mặt bằng 36, độ dài đường chéo bằng 6. Thể tích lớn nhất của hình hộp chữ nhật đã cho là

V_{\max} = 8.

V_{\max} = 12 .

V_{\max} = 8 \sqrt{2} .

V_{\max} = 6 \sqrt{6} .

Câu 247: 1 điểm

Cho hai đường thẳng cố định a và b chéo nhau. Gọi AB là đoạn vuông góc chung của a và b $(A \in a; B \in b)$ . Trên a lấy điểm M (khác A), trên b lấy điểm N (khác B) sao cho $A M = x, B N = y, x + y = 8$ . Biết AB = 6, góc giữa hai đường thẳng a và b bằng $60 °$ . Khi thể tích khối tứ diện ABNM đạt giá trị lớn nhất thì độ dài đoạn MN (biết $M N > 8$ ) là

13.

12.

2 \sqrt{39} .

2 \sqrt{21} .

Câu 248: 1 điểm

Cho hình hộp chữ nhật có kích thước $m \times n \times p$ (với m,n,p là các số nguyên dương và $m \leq n \leq p$ ). Biết rằng thể tích hình hộp chữ nhật đã cho bằng $\frac{1}{2}$ thể tích hình hộp chữ nhật có kích thước $(m + 2) \times (n + 2) \times (p + 2)$ . Giá trị lớn nhất có thể có của p là

30.

130.

120.

Câu 249: 1 điểm

Cho hình chóp SABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Biết $S A = a, A B = b .$ Khoảng cách từ điểm A đến mặt phẳng (SBC) là

\frac{a + b}{\sqrt{a^{2} + b^{2}}} .

\frac{2 a b}{\sqrt{a^{2} + b^{2}}} .

\frac{a b}{2 \sqrt{a^{2} + b^{2}}} .

\frac{a b}{\sqrt{a^{2} + b^{2}}} .

Câu 250: 1 điểm

Cho tứ diện đều cạnh bằng 1 và điểm I nằm trong tứ diện.Tổng khoảng cách từ I đến các mặt của tứ diện là

\sqrt{6} .

\frac{\sqrt{6}}{9} .

\frac{\sqrt{3}}{2} .

\frac{\sqrt{6}}{3} .

Câu 251: 1 điểm

Cho hình hộp chữ nhật ABCD.A'B'C'D' có $A B = 3, A D = 4, A A^{'} = 5$ . Lấy điểm M trên cạnh AB sao cho $B M = 4 A M$ . Khoảng cách từ C' đến BD bằng 4. Khoảng cách từ điểm M đến $(B C^{'} D)$ là

\frac{12}{5}

\frac{3 \sqrt{3}}{2}

\frac{8}{3}

Câu 252: 1 điểm

Cho tứ diện ABCD có $A B = C D = 4, A C = B D = 5, A D = B C = 6.$ Khoảng cách từ A đến mặt phẳng (BCD) là

\frac{3 \sqrt{6}}{7} .

\frac{3 \sqrt{2}}{5} .

\frac{3 \sqrt{42}}{7} .

\frac{\sqrt{7}}{2} .

Câu 253: 1 điểm

Cho hình chóp S.ABC có $S A = 2, S B = 3, S C = 4$ .Góc $\hat{A S B} = 45 °, \hat{B S C} = 60 °, \hat{C S A} = 90 °$ . Tính khoảng cách d giữa hai đường thẳng SA và BC.

\frac{6 \sqrt{34}}{17} .

\frac{4 \sqrt{34}}{17} .

\frac{7 \sqrt{34}}{17} .

\frac{3 \sqrt{34}}{17} .

Câu 254: 1 điểm

Cho tứ diện ABCD có thể tích bằng V. Trên AB lấy hai điểm M, N trên CD lấy hai điểm P, Q thỏa mãn $2 \frac{M N}{C D} + 3 \frac{P Q}{A B} = 1$ . Thể tích khối MNPQ đạt giá trị lớn nhất bằng

\frac{V}{8}

\frac{V}{16} .

\frac{V}{24} .

\frac{V}{32} .

Câu 255: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a. M, N lần lượt là trung điểm của AB và AD, H là giao điểm của CN với MD. Biết $S H ⊥ (A B C D), S H = a \sqrt{3}$ . Khoảng cách giữa DM và SC là

\frac{3 a \sqrt{57}}{38} .

\frac{2 a \sqrt{57}}{19} .

\frac{3 a \sqrt{57}}{19} .

\frac{2 a \sqrt{57}}{27} .

Câu 256: 1 điểm

Cho hình chóp SABCD có đáy ABCD là hình vuông, SA vuông góc với đáy, mặt bên (SCD) tạo với mặt đáy một góc bằng $60 °$ , M là trung điểm BC. Biết thể tích khối chóp SABCD bằng $\frac{a^{3} \sqrt{3}}{3} .$ Khoảng cách từ điểm M đến mặt phẳng (SCD) là

\frac{a \sqrt{3}}{6} .

a \sqrt{3} .

\frac{a \sqrt{3}}{4} .

\frac{a \sqrt{3}}{2} .

Câu 257: 1 điểm

Cho khối chóp S.ABC có thể tích bằng $24 c m^{3}, S B = B C = 5 c m, S C = 8 c m .$ Khoảng cách từ điểm A đến mặt phẳng (SBC) là

3 cm.

4 cm.

6 cm.

12 cm.

Câu 258: 1 điểm

Cho khối chóp SABCD có thể tích $V = 6 a^{3}$ , đáy ABCD là hình thang với hai đáy AD và BC thỏa mãn $A D = 2 B C$ , diện tích tam giác SCD bằng $\sqrt{34} a^{2}$ . Khoảng cách từ B đến (SCD) là

\frac{3 \sqrt{34}}{34} a .

\frac{9 \sqrt{34}}{17} a .

\frac{\sqrt{34}}{17} a .

\frac{3 \sqrt{34}}{17} a .

Câu 259: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C' có $A B = a, A C = 2 a, A A^{'} = 2 a \sqrt{5}$ và $\hat{B A C} = 120 ° .$ Gọi K,I lần lượt là trung điểm của các cạnh CC',BB' . Khoảng cách từ điểm I đến mặt phẳng $(A^{'} B K)$ là

\frac{a \sqrt{5}}{6}

\frac{a \sqrt{5}}{3}

a \sqrt{15}

\frac{a \sqrt{15}}{3}

Câu 260: 1 điểm

Cho hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$ có cạnh a. Khoảng cách giữa đường thẳng $A_{1} B$ và $B_{1} D$ là

\frac{a \sqrt{3}}{6} .

\frac{a \sqrt{2}}{3} .

\frac{a \sqrt{6}}{6} .

\frac{a \sqrt{6}}{3} .

Câu 261: 1 điểm

Cho hình chóp S.ABC có hình chiếu vuông góc của điểm S nằm trong tam giác ABC. Tam giác ABC có bán kính đường tròn nội tiếp $r = 3, B C = 5$ và diện tích tam giác ABC là S = 10. Các mặt bên của hình chóp S.ABC đều tạo với đáy các góc bằng nhau và bằng $60 °$ . Khoảng cách h từ điểm A đến mặt phẳng (SBC) là

h = 2 \sqrt{3} .

h = \sqrt{3} .

h = 3 \sqrt{3} .

h = \frac{\sqrt{3}}{2} .

Câu 262: 1 điểm

Cho tứ diện ABCD có $A B = 3 a, A C = 2 a, A D = 5 a; \hat{B A C} = \hat{C A D} = \hat{D A B} = 60 °$ . Khoảng cách từ C đến (ABD) là

\frac{2 a \sqrt{6}}{3} .

\frac{a \sqrt{6}}{9} .

\frac{a \sqrt{6}}{3} .

\frac{2 a \sqrt{6}}{9} .

Câu 263: 1 điểm

Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng $a \sqrt{2}$ . Tam giác SAD cân tại S và mặt bên (SAD) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng $\frac{4}{3} a^{3}$ . Khoảng cách h từ B đến mặt phẳng (SCD) là

h = \frac{2}{3} a .

h = \frac{4}{3} a .

h = \frac{8}{3} a .

h = \frac{3}{4} a .

Câu 264: 1 điểm

Cho hình chóp đều S.ABC có độ dài đường cao từ đỉnh S đến mặt phẳng đáy (ABC) bằng $\frac{a \sqrt{21}}{7}$ . Góc tạo bởi mặt bên với mặt phẳng đáy bằng $60 °$ . Gọi M, N lần lượt là trung điểm của AB, SC. Khoảng cách giữa hai đường thẳng SA, MN là

\frac{9 a \sqrt{3}}{42} .

\frac{3 a \sqrt{3}}{42} .

\frac{6 a \sqrt{3}}{42} .

\frac{12 a \sqrt{3}}{42} .

Câu 265: 1 điểm

Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A' trên đáy (ABC) trùng với trọng tâm của tam giác ABC . Biết thể tích của khối lăng trụ là $\frac{a^{3} \sqrt{3}}{4}$ . Khoảng cách giữa hai đường thẳng AA' và BC là

\frac{3 a}{2}

\frac{4 a}{3}

\frac{3 a}{4}

\frac{2 a}{3}

Câu 266: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S trên (ABC) là điểm H thuộc cạnh AB sao cho HA = 2HB. Góc giữa đường thẳng SC và (ABC) bằng $60 °$ .Khoảng cách giữa hai đường thẳng SA và BC là

\frac{a \sqrt{21}}{4} .

\frac{a \sqrt{42}}{24} .

\frac{a \sqrt{21}}{8} .

\frac{a \sqrt{42}}{8} .

Câu 267: 1 điểm

Cho khối tứ diện ABCD có thể tích $V = \frac{1}{6}$ , góc $\hat{A C B} = 45 °$ và $A D + B C + \frac{A C}{\sqrt{2}} = 3$ . Độ dài cạnh CD là

2 \sqrt{3} .

\sqrt{3} .

\sqrt{2} .

Câu 268: 1 điểm

Cho hình chóp SABCD có đáy là hình thoi tâm O cạnh a, $\hat{A B C} = 60 °, S A = S B = S C = 2 a .$ Khoảng cách giữa AB và SC là

\frac{a \sqrt{11}}{12} .

\frac{a \sqrt{22}}{4} .

\frac{a \sqrt{11}}{4} .

\frac{a \sqrt{22}}{12} .

Câu 269: 1 điểm

Kim tự tháp Cheops ( có dạng hình chóp đều) là kim tự tháp cao nhất ở Ai Cập. Đáy của kim tự tháp là hình vuông có cạnh dài 230m. Các lối đi và phòng bên trong chiếm 30%, khối lượng riêng của đá bằng 2,5.103 kg/m3. Khối lượng đá tạo nên kim tự tháp là 4 443 600 tấn.

Chiều cao kim tự tháp là:

148m

144m

154m

156m

Câu 270: 1 điểm

Một công ty sữa cần sản xuất các hộp đựng sữa dạng hình hộp chữ nhật có đáy là hình vuông, chứa được thể tích thực là 180ml. Chiều cao của hình hộp bằng bao nhiêu để nguyên liệu sản xuất vỏ hộp là ít nhất?

\sqrt[3]{180^{2}}

(cm)

\sqrt[3]{360}

(cm)

\sqrt[3]{720}

(cm)

\sqrt[3]{180}

(cm)

Câu 271: 1 điểm

Cho một tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x(cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất

x = 6

x = 3

x = 2

x = 4

Câu 272: 1 điểm

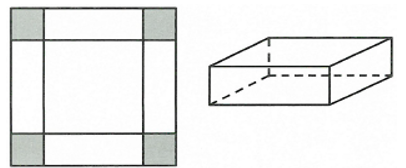
Một xưởng sản xuất những thùng bằng nhôm hình hộp chữ nhật không nắp và có các kích thước x, y, z (dm). Biết tỉ số hai cạnh đáy là $x : y = 1 : 3$ , thể tích khối hộp bằng 18dm3. Để tốn ít vật liệu nhất thì tổng x + y + z bằng:

10 dm

\frac{19}{2} d m

26 dm

\frac{26}{3} d m

Câu 273: 1 điểm

Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp. Nếu dung tích của cái hộp đó là 4800 cm3 thì cạnh của tấm bìa có độ dài là

38cm

42cm

36cm

44cm

Câu 274: 1 điểm

Một hồ bơi có dạng hình hộp chữ nhật có chiều dài 50 m, chiều rộng 30 m. Biết rằng trong hồ bơi có 3 000 000 lít nước. Độ sâu của hồ bơi lúc này là

2,5m

Câu 275: 1 điểm

Một hộp sữa tươi dạng hình hộp chữ nhật có thể tích thực của sữa là 180ml, người ta để khoảng không gian trống cho không khí vào bằng 10% thể tích của sữa. Đáy hộp là hình chữ nhật có diện tích 16,5cm2.Biết độ dày hộp giấy không đáng kể. Hỏi chiều cao hộp sữa bằng bao nhiêu?

\frac{108}{11}

10 cm

\frac{400}{33}

12cm

Câu 276: 1 điểm

Tháp Eiffel ở Pháp cao 300m, được làm hoàn toàn bằng sắt và nặng khoảng 8 000 000 kg.

Người ta làm một mô hình thu nhỏ của tháp với cùng chất liệu và cân nặng 1kg. Hỏi chiều cao của mô hình là bao nhiêu?

1,5m

0,5m

Câu 277: 1 điểm

Một tấm nhôm hình chữ nhật ABCD có AD = 24 cm.Ta gấp tấm nhôm theo hai cạnh MN và QP vào phía trong đến khi AB và CD trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết hai đáy.

Một tấm nhôm hình chữ nhật ABCD có AD = 24 cm.Ta gấp tấm nhôm theo hai cạnh (ảnh 1)

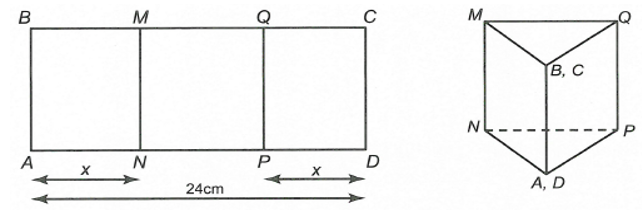
Tìm x để thể tích khối lăng trụ lớn nhất.

x = 9

x = 8

x = 10

x = 6

Câu 278: 1 điểm

Từ một mảnh giấy hình vuông cạnh a, người ta gấp thành hình lăng trụ theo hai cách sau.

+) Cách 1. Gấp thành 4 phần đều nhau rồi dựng lên thành một hình lăng trụ tứ giác đều có thể tích là V1 (Hình 1)

+) Cách 2. Gấp thành 3 phần đều nhau rồi dựng lên thành một hình lăng trụ tam giác đều có thể tích là V2 (Hình 2)

Từ một mảnh giấy hình vuông cạnh a, người ta gấp thành hình lăng trụ theo hai cách sau (ảnh 1)

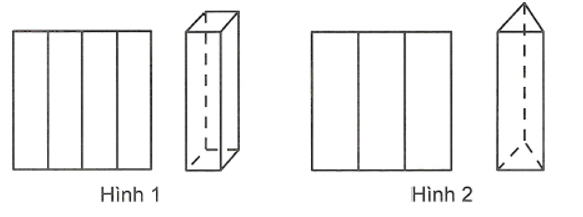
Tính tỷ số k = $\frac{V_{1}}{V_{2}}$

k = \frac{3 \sqrt{3}}{2}

k = \frac{4 \sqrt{3}}{9}

k = \frac{3 \sqrt{3}}{4}

k = \frac{3 \sqrt{3}}{8}

Câu 279: 1 điểm

Cắt một miếng giấy hình vuông ở hình 1 và xếp thành một hình chóp tứ giác đều như hình 2.Biết cạnh hình vuông bằng 20 cm, OM = x (cm).

Cắt một miếng giấy hình vuông ở hình 1 và xếp thành một hình chóp tứ giác đều như hình 2 (ảnh 1)

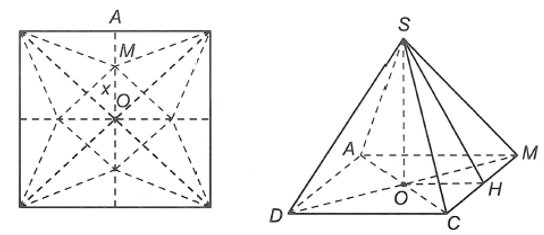
Tìm x để hình chóp đều ấy có thể tích lớn nhất.

x = 6 cm

x = 8 cm

x = 7 cm

x = 9 cm

Câu 280: 1 điểm

Từ một tấm bìa hình vuông ABCD có cạnh bằng 5dm, người ta cắt bỏ bốn tam giác cân bằng nhau là và DQA . Với phần còn lại, người ta gấp lên và ghép lại để thành hình chóp tứ giác đều. Hỏi cạnh đáy của khối chóp bằng bao nhiều để thể tích của nó là lớn nhất?

Từ một tấm bìa hình vuông ABVD có cạnh bằng 5dm, người ta cắt bỏ bốn tam giác cân bằng nhau là và (ảnh 1)

\frac{3 \sqrt{2}}{2}

\frac{5}{2}

2 \sqrt{2}

\frac{5 \sqrt{2}}{2}

Câu 281: 1 điểm

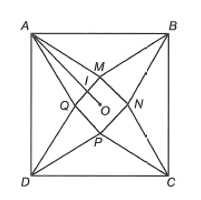
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. ( Giả thuyết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá đầu).

\frac{2 a^{2}}{\sqrt{3}}

\frac{a^{2}}{\sqrt[3]{2}}

\frac{a^{2}}{4}

\frac{a^{2}}{\sqrt[3]{4}}

Câu 282: 1 điểm

Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 200 m3. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng. Chi phí để xây bể là 300 nghìn đồng/m2 (chi phí được tính theo diện tích xây dựng, bao gồm diện tích đáy và diện tích xung quanh, không tính chiều dày của đáy và thành bể). Hãy xác định chi phí thấp nhất để xây bể ( làm tròn đến đơn vị triệu đồng).

75 triệu đồng

51 triệu đồng

36 triệu đồng

46 triệu đồng

Câu 283: 1 điểm

Người ta cần lợp tôn cho mái nhà như hình vẽ. Biết mái trước, mái sau là các hình thang cân ABCD, ABEF ; hai đầu hồi là hai tam giác cân

A D E, B C F

tại A và B. Hình chiếu vuông góc của A trên mặt phẳng là H.Biết

A B = 16 m, C D = F E = 20 m, A H = 1,73 m, E D = C F = 6 m

Tính tổng diện tích S của mái nhà ( diện tích của hai mái trước, sau và hai đầu hồi).

$S \approx 141$ m²

S \approx 281

m²

S \approx 261

m²

S \approx 78

m²

Câu 284: 1 điểm

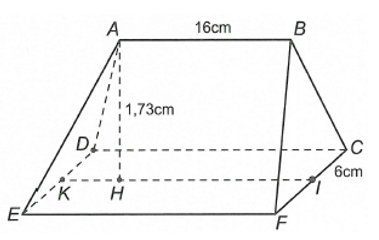
Cắt ba góc của một tam giác đều cạnh bằng a các đoạn bằng x, $0 < x < \frac{a}{2}$ ; phần còn lại là một tam giác đều bên ngoài là các hình chữ nhật, rồi gấp các hình chữ nhật lại tạo thành khối lăng trụ tam giác đều như hình vẽ.

Tìm độ dài x để thể tích khối lăng trụ lớn nhất.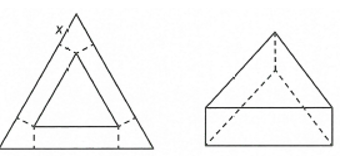

Cắt ba góc của một tam giác đều cạnh bằng a các đoạn bằng x, 0 nhỏ hơn x nhỏ hơn a/2 ; phần còn lại là một (ảnh 1)

\frac{a}{3}

\frac{a}{4}

\frac{a}{5}

\frac{a}{6}

Câu 285: 1 điểm

Từ hình vuông có cạnh bằng 6, người ta cắt bỏ các tam giác vuông cân tạo thành hình tô đậm như hình vẽ. Sau đó người ta gập thành hình hộp chữ nhật không nắp. Thể tích lớn nhất của khối hộp là

A. $8 \sqrt{2}$

10 \sqrt{2}

9 \sqrt{2}

11 \sqrt{2}

Câu 286: 1 điểm

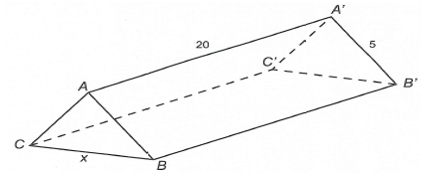
Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng như hình vẽ. Hai mặt bên ABB'A' và ACC'A' là hai tấm kính hình chữ nhật dài 20 (m) và rộng 5 (m). Gọi x (mét) là độ dài của cạnh BC. Tìm x để khoảng không gian của hành lang (kể cả hai tấm kính) là lớn nhất ?

Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng như hình vẽ. Hai mặt bên (ảnh 1)

x = 5 (m)

x = 5 \sqrt{2} (m)

x = 5 \sqrt{17} (m)

x = 25 (m)

Câu 287: 1 điểm

Để thiết kế một chiếc bể cá hình hộp chữ nhật không có nắp có chiều cao là 60 cm, thể tích 96000 cm3. Người thợ dùng loại kính để sử dụng làm mặt bên có giá thành 70 000 đồng/m2 và loại kính để làm mặt đáy có giá thành 100 000 đồng/m2. Tính chi phí thấp nhất để hoàn thành bể cá.

320 000 đồng

32 000 đồng

83 200 đồng

68 800 đồng

Câu 288: 1 điểm

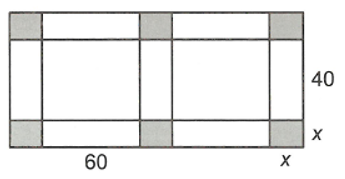
Cho một tấm bìa hình chữ nhật có kích thước 60 cm x 40 cm. Người ta cắt 6 hình vuông bằng nhau như hình vẽ, mỗi hình vuông cạnh bằng x cm, rồi gập tấm bìa lại để được một hộp có nắp. Tìm x để hộp nhận được có thể tích lớn nhất.

x = \frac{20}{3} c m

x = 4 c m

x = 5 c m

x = \frac{10}{3} c m

Câu 289: 1 điểm

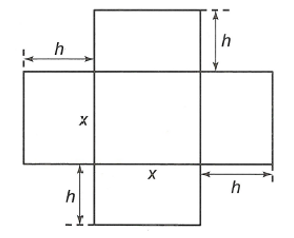
Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh x cm, chiều cao là h cm và thể tích là 500 cm³. Tìm độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.

Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh x cm, chiều cao là h cm và thể tích là 500 cm3. Tìm độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa các tông nhất (ảnh 1)

x = 2 cm

x = 3 cm

x = 5 cm

x = 10 cm

Câu 290: 1 điểm

Một trang chữ của cuốn sách giáo khoa cần diện tích 384 cm². Lề trên và dưới là 3 cm, lề trái và phải là 2 cm. Kích thước tối ưu của trang giấy là

Một trang chữ của cuốn sách giáo khoa cần diện tích 384 cm^2. Lề trên và dưới là 3 cm, lề trái và phải là 2 cm. Kích thước tối ưu của trang giấy là (ảnh 1)

Dài 24 cm; rộng 16 cm

Dài 24 cm; rộng 17 cm

Dài 25 cm; rộng 15,36 cm

Dài 25.6 cm; rộng 15 cm

Câu 291: 1 điểm

Một trang trại chăn nuôi dự định xây dựng một hầm biogas với thể tích 12m³ để chứa chất thải chăn nuôi và tạo khí sinh học. Dự kiến hầm chứa có dạng hình hộp chữ nhật có chiều sâu gấp rưỡi chiều rộng. Hãy xác định các kích thước đáy (dài, rộng) của hầm biogas để thi công tiết kiệm nguyên vật liệu nhất (không tính đến bề dày của thành bể). Ta có kích thước (dài ; rộng – tính theo đơn vị m, làm tròn đến 1 chữ số thập phân sau dấu phẩy) phù hợp yêu cầu là

Dài 2,42 m và rộng 1,82m

Dài 2,74m và rộng 1,71m

Dài 2,26 m và rộng 1,88 m

Dài 2,19m và rộng 1,91m

Câu 292: 1 điểm

Một công ty sản xuất gỗ muốn thiết kế các thùng đựng hàng bên trong dạng hình lăng trụ tứ giác đều không nắp có thể tích là 62,5dm². Để tiết kiệm vật liệu làm thùng, người ta cần thiết kế thùng sao cho có tổng S diện tích xung quanh và diện tích mặt đáy là nhỏ nhất. Khi đó tổng diện tích S bằng

106,25 dm²

75 dm²

50 \sqrt{5}

dm²

125 dm²

Câu 293: 1 điểm

Khi xây dựng nhà, chủ nhà cần làm một bể nước bằng gạch có dạng hình hộp có đáy là hình chữ nhật chiều dài d (m) và chiều rộng r (m) với d = 2r. Chiều cao bể nước là h (m) và thể tích bể là 2m³. Hỏi chiều cao bể nước như thế nào thì chi phí xây dựng là thấp nhất?

\frac{3}{2} \sqrt{\frac{3}{2}} (m)

\sqrt[3]{\frac{2}{3}} (m)

\sqrt[3]{\frac{3}{2}} (m)

\frac{2}{3} \sqrt{\frac{2}{3}} (m)

Câu 294: 1 điểm

Bác An cần xây một bể đựng nước mưa có thể tích $V = 6 (m^{3})$ dạng hình hộp chữ nhật với chiều dài gấp ba lần chiều rộng, đáy và nắp đổ bể tông, cốt thép ; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 1 triệu đồng/m2 và ở nắp để hở một khoảng hình vuông có diện tích bằng $\frac{2}{9}$ diện tích nắp bể. Chi phí thấp nhất mà bác An phải trả là

20 triệu đồng

20,5 triệu đồng

21 triệu đồng

22 triệu đồng

Câu 295: 1 điểm

Cho một khối lập phương có cạnh bằng 1m. Biết rằng chiều cao mực nước trong khối lập phương là 0,6m. Hỏi khi đặt khối lập phương đứng ở vị trí đứng cân bằng trên một cạnh như hình vẽ thì chiều cao h mực nước tính từ mặt phẳng đạt là bao nhiêu ?

h = \frac{2 \sqrt{7} + 25 \sqrt{2}}{50} m

h = \frac{5 \sqrt{2} - \sqrt{10}}{5} m

h = \frac{4}{5} m

h = \frac{5 \sqrt{2} - 3}{5} m

Câu 296: 1 điểm

Một người xây nhà xưởng hình hộp chữ nhật có diện tích mặt sàn là 1152m² và chiều cao cố định. Người đó xây các bức tường xung quanh và bên trong để ngăn nhà xưởng thành ba phòng hình chữ nhật có kích thước như nhau (không kể trần nhà). Vậy cần phải xây các phòng theo kích thước nào để tiết kiệm chi phí nhất (bỏ qua độ dày các bức tường).

Một người xây nhà xưởng hình hộp chữ nhật có diện tích mặt sàn là 1152m2 và chiều cao cố định. Người đó xây các bức tường xung quanh và bên trong để ngăn nhà xưởng thành ba phòng hình chữ nhật có kích thước như nhau (không kể trần nhà). Vậy cần phải xây các phòng theo kích thước nào để tiết kiệm chi phí nhất (bỏ qua độ dày các bức tường). (ảnh 1)

16m x 24m

8m x 48m

12m x 32m

24m x 32m

Câu 297: 1 điểm

Một kim tự tháp Ai Cập có hình dạng là một khối chóp tứ giác đều có độ dài cạnh bên là một số thực dương không đổi. Gọi α là góc giữa cạnh bên của kim tự tháp và mặt đáy. Khi thể tích của kim tự tháp lớn nhất, tính sinα

sinα

= \frac{\sqrt{6}}{3}

sinα

= \frac{\sqrt{3}}{3}

sinα

= \frac{\sqrt{5}}{3}

sinα

= \frac{\sqrt{3}}{2}

Câu 298: 1 điểm

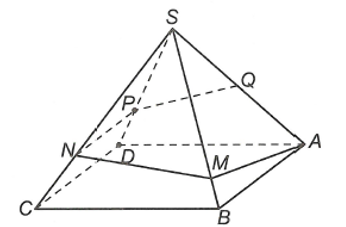
Bên cạnh con đường trước khi vào thành phố người ta xây một tháp đèn lộng lẫy. Ngọn tháp hình tứ giác đều SABCD cạnh bên $S A = 600$ mét, $\hat{A S B} = 15 °$ . Do có sự cố đường dây điện tại điểm Q ( là trung điểm của SA) bị hỏng, người ta tạo ra một con đường từ A đến Q gồm bốn đoạn thẳng, $A M, M N, N P, P Q$ (hình vẽ). Để tiết kiệm kinh phí, kỹ sư đã nghiên cứu và có được chiều dài con đường từ A đến Q ngắn nhất. Tính tỷ số $k = \frac{A M + M N}{N P + P Q}$

Bên cạnh con đường trước khi vào thành phố người ta xây một tháp đèn lộng lẫy. Ngọn tháp hình tứ giác đều (ảnh 1)

k = \frac{5}{3}

k = \frac{3}{2}

k = \frac{4}{3}

k = 2

Câu 299: 1 điểm

Cho hình lập phương ABCD.A'B'C'D' cạnh bằng 1, M là trung điểm cạnh AB. Một con kiến đi từ điểm M thẳng tới điểm N thuộc cạnh BC , từ điểm N đi thẳng tới điểm P thuộc cạnh CC',từ điểm P đi thẳng tới điểm D'( điểm N,P thay đổi tùy theo hướng đi của con kiến). Quãng đường ngắn nhất để con kiến đi từ M đến D' là

\frac{5}{2}

\sqrt{2} + 1

\frac{7}{2}

\frac{3}{2} + \sqrt{2}

Xem thêm đề thi tương tự

Chuyên đề Toán 12 Bài 3: Ứng dụng của tích phân có đáp ánLớp 12Toán

Chuyên đề Toán 12
Chuyên đề 3: Nguyên hàm - Tích phân
Lớp 12;Toán

23 câu hỏi 1 mã đề 1 giờ

182,280 lượt xem 98,140 lượt làm bài