
Chuyên đề Toán 12 Bài 5: Phương trình lôgarit - Bất phương trình lôgarit có đáp án
Chuyên đề Toán 12 <br> Chuyên đề 2: Logarit <br> Lớp 12;Toán <br>
Đề thi nằm trong bộ sưu tập: TOÁN 12
Số câu hỏi: 188 câuSố mã đề: 1 đềThời gian: 1 giờ
180,159 lượt xem 13,850 lượt làm bài
Xem trước nội dung:
Số nghiệm của phương trình là
Cho phương trình . Tổng tất cả các nghiệm của phương trình là
Cho phương trình . Gọi a là nghiệm của phương trình, biểu thức nào sau đây là đúng?
Tìm nghiệm của phương trình .
Phương trình có hai nghiệm . Khi đó bằng
Phương trình có
Phương trình có bao nhiêu nghiệm?
Phương trình có tổng bình phương các nghiệm bằng
Số nghiệm của phương trình là
Số nghiệm của phương trình là
Biết rằng phương trình có nghiệm duy nhất . Khẳng định nào dưới đây đúng?
Xét các số nguyên dương a,b sao cho phương trình có hai nghiệm phân biệt và phương trình có hai nghiệm phân biệt thỏa mãn . Tính giá trị nhỏ nhất của S = 2a + 3b.
Phương trình có tất cả bao nhiêu nghiệm phân biệt?
Biết phương trình có hai nghiệm phân biệt. Khi đó tích hai nghiệm này bằng
Tổng tất cả các nghiệm của phương trình bằng
Phương trình có tất cả bao nhiêu nghiệm?
Tổng các nghiệm của phương trình là một số có dạng với a,b là các số nguyên dương. Giá trị của a + b là
Có bao nhiêu giá trị nguyên của tham số để phương trình có nghiệm?
Có bao nhiêu giá trị nguyên của tham số để phương trình có nghiệm ?
Có bao nhiêu giá trị nguyên của tham số để phương trình có nghiệm thực duy nhất?
Có bao nhiêu giá trị nguyên của tham số để phương trình có hai nghiệm thực phân biệt trong khoảng ?
Có bao nhiêu giá trị nguyên của tham số m để có nghiệm trong đoạn ?
Tìm các giá trị của tham số m để phương trình có nghiệm thuộc khoảng .
Có bao nhiêu giá trị nguyên của tham số để phương trình có hai nghiệm thỏa mãn ?
Nghiệm phương trìnhlà
Tổng các nghiệm không âm của phương trình là
Phương trình tương đương với phương trình nào sau đây?
Cho phương trình , số nghiệm của phương trình trên là
Phương trình có bao nhiêu nghiệm?
Một học sinh giải phương trình theo các bước như sau:
Bước 1: Điều kiện
Bước 2: Từ điều kiện trên phương trình đã cho trở thành:
Bước 3: Vậy nghiệm phương trình là (nhận)
Lời giải trên sai ở bước nào?
Phương trình có bao nhiêu nghiệm?
Nghiệm của phương trình là?
Với giá trị m bằng bao nhiêu thì phương trình có nghiệm là -1?
Phương trình có nghiệm là
Tập nghiệm của phương trình là
Tất cả các giá trị x thỏa mãn là
Với giá trị nào của m thì phương trình có hai nghiệm phân biệt?
Phương trình có
Phương trình có nghiệm là
Cho phương trình , tổng bình phương các nghiệm của phương trình trên là
Với giá trị nào của m thì phương trình có nghiệm trên [1;3]?
Tìm tổng các nghiệm của phương trình
Tập nghiệm của phương trình là
Giải phương trình ta được nghiệm
Tập nghiệm của phương trình là
Tập nghiệm của phương trình là
Tập nghiệm của phương trình là
Phương trình có tập nghiệm là
Tập nghiệm của phương trình là
Tập nghiệm của phương trình là
Tìm số nghiệm của phương trình
Tìm số nghiệm của phương trình
Tìm số nghiệm của phương trình
Tìm số nghiệm của phương trình
Tìm số nghiệm của phương trình
Tìm số nghiệm của phương trình
Phương trình có số nghiệm là
Giải phương trình ta được nghiệm x = a. Khi đó giá trị a thuộc khoảng nào sau đây?
Phương trình có nghiệm nguyên dương là a. Tính giá trị của biểu thức
Tập nghiệm của phương trình là
Số nghiệm của phương trình là
Tìm m để phương trình có ba nghiệm thực phân biệt.
Tìm m để phương trình có đúng hai nghiệm phân biệt.
Nghiệm của phương trình là
Tìm tích các nghiệm của phương trình
Cho phương trình có nghiệm với là phân số tối giản. Khi đó tổng a + b bằng?
Phương trình có bao nhiêu nghiệm?
Gọi Tlà tổng các nghiệm của phương trình . Tính T
Hiệu của nghiệm lớn nhất với nghiệm nhỏ nhất của phương trình là
Phương trình có nghiệm là
Phương trình có ba nghiệm phân biệt khi và chỉ khi , đặt thì
Cho phương trình với mlà tham số thực. Gọi Slà tập các giá trị của mđể phương trình có nghiệm. Khi đó Scó dạng . Tính
Tìm tất cả các giá trị của m để phương trình có hai nghiệm thực phân biệt thuộc
Tìm tất cả các giá trị của tham số m để phương trình có 2 nghiệm sao cho
Định điều kiện cho tham số m để có nghiệm.
Số nghiệm của phương trình là
Nghiệm phương trình là
Biết rằng phương trình có hai nghiệm phân biệt . Tính
Tìm tập nghiệm S của phương trình .
Biết rằng phương trình có hai nghiệm và . Hãy tính tổng
Số nghiệm của phương trình là
Biết rằng phương trình có nghiệm duy nhất dạng với . Tính tổng S = a + b
Phương trình có tổng các nghiệm bằng:
Gọi S là tổng các giá trị nguyên của tham số m sao cho phương trình vô nghiệm. Giá trị của S bằng
Tìm các giá trị thực của tham số m để phương trình có nghiệm duy nhất
Tìm các giá trị thực của tham số m để phương trình có nghiệm duy nhất
Tìm giá trị thực của tham số m để phương trình có nghiệm duy nhất nhỏ hơn 1.
Gọi là giá trị thực nhỏ nhất của tham số m sao cho phương trình có nghiệm thuộc (2;4). Mệnh đề nào sau đây là đúng?
Tìm các giá trị thực của tham số m để phương trình có nghiệm duy nhất
Cho phương trình với m là tham số thực. Tìm các giá trị của m để phương trình có nghiệm thuộc
Có bao nhiêu giá trị m nguyên thuộc để phương trình có nghiệm duy nhất?
Tìm các giá trị của tham số m để phương trình có nghiệm.
Cho phương trình với m là tham số thực. Tìm tất cả các giá trị của m để phương trình có đúng hai nghiệm phân biệt.
Cho phương trình với m là tham số thực. Gọi Slà tập tất cả các giá trị của mmđể phương trình có nghiệm duy nhất, khi đó Scó dạng với . Tính
Tập nghiệm của bất phương trình có dạng , với là phân số tối giản và alà số nguyên. Tính a + b + c
Tập nghiệm của bất phương trình là . Tính a + 3b
Tìm số nghiệm nguyên của bất phương trình
Bất phương trình có tập nghiệm là
Số nghiệm nguyên của bất phương trình là
Tập nghiệm của bất phương trình là , với . Tính
Bất phương trình có tập nghiệm là . Tính tổng a + b + c + d
Biết tập nghiệm S của bất phương trình là khoảng (a;b). Tính b - a
Có bao nhiêu giá trị nguyên thỏa mãn bất phương trình ?
Biết rằng bất phương trình có tập nghiệm là , với a,b là các số nguyên dương nhỏ hơn 6 và . Tính
Tập nghiệm của bất phương trình có dạng là với a,b,c,dlà các số nguyên dương. Tính tổng a + b + c + d
Có bao nhiêu giá trị nguyên của tham số để bất phương trình nghiệm đúng với mọi
Có bao nhiêu giá trị nguyên của tham số để bất phương trình nghiệm đúng với mọi
Số giá trị nguyên của tham số m để bất phương trình nghiệm đúng với mọi x là
Tìm tập nghiệm của bất phương trình
Tập nghiệm của bất phương trình là
Tìm tập nghiệm S của bất phương trình
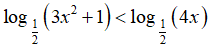
Tập nghiệm của bất phương trình là
Tập nghiệm của bất phương trình là
Với m là tham số thực dương khác 1. Hãy tìm tập nghiệm S của bất phương trình , biết rằng x= 1 là một nghiệm của bất phương trình.
Tập xác định của hàm số là
Bất phương trình tương đương với bất phương trình nào sau đây?
Tất cả các giá trị của m để bất phương trình có nghiệm đúng với mọi giá trị của x là
Có bao nhiêu số nguyên dương x thỏa mãn điều kiện ?
Tập nghiệm của bất phương trình là
Bất phương trình là
Bất phương trình có tập nghiệm là
Tập nghiệm của bất phương trình là
Tập nghiệm của bất phương trình là
Bất phương trình có tập nghiệm là
Cho bất phương trình . Nghiệm của bất phương trình đã cho là
Cho bất phương trình . Nghiệm của bất phương trình đã cho là
Tập nghiệm của bất phương trình là
Tập nghiệm của bất phương trình chứa khoảng nào dưới đây?
Bất phương trình có tập nghiệm là
Nghiệm của bất phương trình là
Nghiệm của bất phương trình là
Nghiệm của bất phương trình là
Nghiệm của bất phương trình là
Giá trị nào của tham số m thì bất phương trình nghiệm đúng với mọi ?
Tập nghiệm S của bất phương trình là
Nghiệm của bất phương trình là
Nghiệm của bất phương trình là
Nghiệm của bất phương trình là
Tập nghiệm của bất phương trình là
Tập nghiệm của bất phương trình là
Tập nghiệm của bất phương trình là
Tìm tập nghiệm S của bất phương trình
Tập nghiệm của bất phương trình là
Tập nghiệm của bất phương trình là
Tập nghiệm của bất phương trình là
Cho bất phương trình . Nếu đặt , ta được bất phương trình nào sau đây?
Tổng các nghiệm nguyên của bất phương trình là
Tập nghiệm của bất phương trình là
Bất phương trình có nghiệm là
Bất phương trình có bao nhiêu nghiệm nguyên trên đoạn
Nghiệm của bất phương trình là
Số nghiệm nguyên của bất phương trình là
Số nghiệm nguyên của bất phương trình là
Mệnh đề nào sau đây đúng khi phát biểu về bất phương trình
Tập nghiệm của bất phương trình là
Tập nghiệm của bất phương trình là
Tập nghiệm của bất phương trình là
Tập nghiệm của bất phương trình là
Tìm m để bất phương trình có nghiệm
Tập nghiệm của bất phương trình là
Số nghiệm nguyên của bất phương trình là
Tập nghiệm của bất phương trình là
Bất phương trình có tập nghiệm
Giải bất phương trình ta được:
Với giá trị nào của tham số m thì bất phương trình có vô số nghiệm
Đề thi tương tự
1 mã đề 51 câu hỏi 1 giờ
186,046 xem14,305 thi
1 mã đề 62 câu hỏi 1 giờ
184,372 xem14,177 thi
5 mã đề 87 câu hỏi 1 giờ
153,965 xem11,835 thi
1 mã đề 58 câu hỏi 1 giờ
151,594 xem11,654 thi
1 mã đề 23 câu hỏi 1 giờ
182,340 xem14,020 thi
1 mã đề 51 câu hỏi 1 giờ
176,690 xem13,586 thi
