Trắc nghiệm Phương trình mũ và phương trình logarit có đáp án

Tìm giá trị của a để phương trình ${\left(2+\sqrt{3}\right)}^x+\left(1-a\right){\left(2-\sqrt{3}\right)}^x$ $-4=0$có 2 nghiệm phân biệt thỏa mãn: $x_1-x_2={\log }_{2+\sqrt{3}}3$, ta có a thuộc khoảng:

Tìm tập hợp tất cả các tham số m sao cho phương trình $4^{x^2-2x+1}-m.2^{x^2-2x+1}+3m-2=0$có 4 nghiệm phân biệt.

Có bao nhiêu số nguyên m thuộc $\left[-2020;2020\right]$sao cho phương trình $4^{{\left(x-1\right)}^2}-4m.2^{x^2-2x}+3m-2=0$có bốn nghiệm phân biệt?

Các giá trị thực của tham số m để phương trình: ${12}^x+\left(4-m\right).3^x-m=0$có nghiệm thuộc khoảng (-1; 0) là

Tích các nghiệm của phương trình ${\left(3+\sqrt{5}\right)}^x+{\left(3-\sqrt{5}\right)}^x=3.2^x$là:

Biết rằng tập hợp các giá trị của m để phương trình ${\left(\frac{1}{4}\right)}^{x^2}-\left(m+1\right).{\left(\frac{1}{2}\right)}^{x^2}-2m=0$có nghiệm, là $\left[-a+2\sqrt{b};0\right]$với a, b là các số nguyên dương. Tính b – a.

Tìm tập nghiệm S của phương trình $3^{x-1}.5^{\frac{2x-2-m}{x-m}}=15$, m là tham số khác 2.

Tìm các giá trị m để phương trình $2^{x+!}=m.2^{x+2}-2^{x+3}$luôn thỏa, $\forall x\in R$

Tính tổng T tất cả các nghiệm của phương trình ${\left(x-3\right)}^{2x^2-5x}=1$

Cho $4^x+4^{-x}=7$. Khi đó biểu thức $P=\frac{5-2^x-2^{-x}}{8+4.2^x+4.2^{-x}}=\frac{a}{b}$với $\frac{a}{b}$tối giản và $a,b\in Z$. Tích a.b có giá trị bằng:

Có bao nhiêu giá trị nguyên dương của tham số m để phương trình ${16}^x-2.{12}^x+\left(m-2\right).9^x=0$có nghiệm dương?

Cho hàm số y=f(x) có bảng biến thiên như sau:

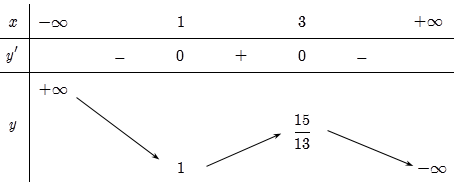
Biết $f\left(0\right)=\frac{7}{6}$, giá trị lớn nhất của m để phương trình $e^{3f^3\left(x\right)-\frac{13}{2}{f}^2\left(x\right)+7f\left(x\right)+\frac{3}{2}}=m$có nghiệm trên đoạn [0;2] là:

Phương trình $2^{23x^3}.2^x-{1024}^{x^2}+23x^3=10x^2-x$có tổng các nghiệm gần nhất với số nào dưới đây

Phương trình $2^{{\log }_5\left(x+3\right)}=x$có tất cả bao nhiêu nghiệm?

Tìm m để phương trình $4^{\sqrt{x+1}+\sqrt{3-x}}-14.2^{\sqrt{x+1}+\sqrt{3-x}}+8=m$có nghiệm

Tính S là tổng tất cả các nghiệm của phương trình $4.2^{2x}-4.2^x+4.2^{-2x}-4.2^{-x}-7=0$

Phương trình $x\left(2^{x-1}+4\right)=2^{x+1}+x^2$có tổng các nghiệm bằng:

Tìm tham số m để tổng các nghiệm của phương trình sau đạt giá trị nhỏ nhất $$\begin{gathered} 1+\left[2x^2-m\left(m+1\right)x-2\right].2^{1+mx-x^2} \\ =\left(x^2-mx-1\right).2^{mx\left(1-m\right)}+x^2-m^{2}x \end{gathered}$$

Cho các số thực không âm x, y, z thỏa mãn $5^x+{25}^y+{125}^z=2020$. Giá trị nhỏ nhất của biểu thức $T=\frac{x}{6}+\frac{y}{3}+\frac{z}{2}$là:

Cho phương trình ${\log }_{3}x.{\log }_{5}x={\log }_{3}x+{\log }_{5}x$. Khẳng định nào sau đây là đúng?

Phương trình ${\left(2+\sqrt{2}\right)}^{{\log }_{2}x}+x{\left(2-\sqrt{2}\right)}^{{\log }_{2}x}$ $=x^2+1$có nghiệm là:

Tìm tập nghiệm của phương trình ${\log }_{3}x+\frac{1}{{\log }_{9}x}=3$

Cho phương trình $2{\log }_4\left(2x^2-x+2m-4m^2\right)$ $+{\log }_{\frac{1}{2}}\left(x^2+mx-2m^2\right)=0$. Tìm tất cả các giá trị của tham số m sao cho phương trình đã cho có hai nghiệm phân biệt $x_1,x_2$thỏa mãn $x_1^2+x_2^2>1$

Tính tổng tất cả các nghiệm thực của phương trình ${\log }_{\sqrt{3}}\left(x-2\right)+{\log }_3{(x-4)}^2=0$

Cho $0\le x\le 2020$và ${\log }_2\left(2x+2\right)+x-3y=8^y$. Có bao nhiêu cặp số (x,y) nguyên thỏa mãn các điều kiện trên?

Phương trình sau đây có bao nhiêu nghiệm $(x^2-4)({\log }_{2}4+{\log }_{3}x+$ ${\log }_{4}x+...+{\log }_{19}x+{\log }_{20}^{2}x=0$

Cho hàm số $f\left(x\right)={\log }_2\left(cosx\right)$. Phương trình f'(x)=0 có bao nhiêu nghiệm trong khoảng $\left(0;2020\mathrm{\pi }\right)$

Có bao nhiêu số nguyên $a\in \left(-2019;2019\right)$để phương trình $\frac{1}{\ln \left(x+5\right)}+\frac{1}{3^x-1}=x+a$có hai nghiệm phân biệt?

Cho phương trình $m\ln \left(x+1\right)-x-2=0$. Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình đã cho có hai nghiệm $x_1,x_2$thỏa mãn $0<x_1<2<4<x_2$là khoảng $\left(a;+\infty \right)$A. Khi đó a thuộc khoảng nào dưới đây?

Cho phương trình ${\log }_2\left(x-\sqrt{x^2-1}\right).{\log }_5\left(x-\sqrt{x^2-1}\right)$ $={\log }_m\left(x+\sqrt{x^2-1}\right)$. Có bao nhiêu giá trị nguyên dương khác 1 của m sao cho phương trình đã cho có nghiệm x lớn hơn 2?

Hỏi phương trình $2{\log }_3\left(cotx\right)={\log }_2\left(\cos x\right)$có bao nhiêu nghiệm trong khoảng $\left(0;2017\mathrm{\pi }\right)$

Có bao nhiêu số nguyên m để phương trình ${\log }_2\frac{3x^2+3x+m+1}{2x^2-x+1}=x^2-5x+2-m$có hai nghiệm phân biệt lớn hơn 1.

Hỏi có bao nhiêu giá trị m nguyên trong đoạn $\left[-2017;2017\right]$để phương trình $\log mx=2\log \left(x+1\right)$có nghiệm duy nhất?

Biết rằng phương trình ${\left[{\log }_{\frac{1}{3}}\left(9x\right)\right]}^2+{\log }_3\frac{x^2}{81}-7=0$có hai nghiệm phân biệt $x_1,x_2$. Tính $x_1.x_2$

Tìm m để phương trình $m\ln (1-x)-\ln x=m$có nghiệm $x\in \left(0;1\right)$

Cho tham số thực a. Biết phương trình $e^x-e^{-x}=2\cos ax$có 5 nghiệm thực phân biệt. Hỏi phương trình $e^x-e^{-x}=2\cos ax+4$có bao nhiêu nghiệm thực phân biệt

Giả sử m là số thực sao cho phương trình ${\log }_3^{2}x-\left(m+2\right){\log }_{3}x+3m-2=0$có hai nghiệm $x_1,x_2$phân biệt thỏa mãn $x_1.x_2=9$.

Khi đó m thỏa mãn tính chất nào sau đây?

Cho phương trình ${\log }_2^{2}x-\left(5m+1\right){\log }_{2}x+4m^2+m=0$. Biết phương trình có 2 nghiệm phân biệt $x_1,x_2$thỏa mãn $x_1+x_2=165$. Giá trị của $\left|x_1-x_2\right|$bằng:

Cho phương trình $m{\ln }^2(x+1)$ $-(x+2-m)\ln (x+1)-x-2=0 \left(1\right)$. Tập tất cả các giá trị của tham số m để phương trình (1) có các nghiệm, trong đó có hai nghiệm phân biệt thỏa mãn $0<x_1<2<4<x_2$là khoảng $\left(a;+\infty \right)$. Khi đó, a thuộc khoảng

Cho x, y là các số thực dương thỏa mãn ${\log }_2\frac{3x+3y+4}{x^2+y^2}$ $=(x+y-1)(2x+2y-1)-4(xy-1)$. Giá trị lớn nhất của biểu thức $P=\frac{5x+3y-2}{2x+y+1}$bằng:

Số nghiệm của phương trình ${\log }_3\left|x^2-\sqrt{2}x\right|={\log }_5\left(x^2-\sqrt{2}x+2\right)$

Phương trình ${\log }_3\frac{x^2-2x+1}{x}+x^2+1=3x$có tổng tất cả các nghiệm bằng:

Cho a, b, c là các số thực dương khác 1 thỏa mãn ${\log }_a^{2}b+{\log }_b^{2}c={\log }_a\frac{c}{b}-2{\log }_b\frac{c}{b}-3$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $P={\log }_{a}b-{\log }_{b}c$. Giá trị của biểu thức S=m-3M bằng:

Cho các số thực a, b, c thuộc khoảng $\left(1;+\infty \right)$và thỏa mãn ${\log }_{\sqrt{a}}^{2}b+{\log }_{b}c.{\log }_b\left(\frac{c^2}{b}\right)$ $+9{\log }_{a}c=4{\log }_{a}b$. Giá trị của biểu thức ${\log }_{a}b+{\log }_b{c}^2$bằng:

Cho phương trình $4^{-\left|x-m\right|}.{\log }_{\sqrt{2}}\left(x^2-2x+3\right)$ $+2^{2x-x^2}.{\log }_{\frac{1}{2}}\left(2\left|x-m\right|+2\right)=0$với m là tham số. Tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là:

Cho các số thực dương a, b, c khác 1 thỏa mãn ${\log }_a^{2}b+{\log }_b^{2}c+2{\log }_b\frac{c}{b}={\log }_a\frac{c}{a^{3}b}$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P={\log }_{a}ab-{\log }_{b}bc$. Tính giá trị của biểu thức $S=2m^2+9M^2$