
Trắc nghiệm Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số có đáp án (Mới nhất)
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số <br> Bài 1: Sự đồng biến, nghịch biến của hàm số <br> Lớp 12;Toán <br>
Đề thi nằm trong bộ sưu tập: TOÁN 12
Số câu hỏi: 65 câuSố mã đề: 1 đềThời gian: 1 giờ
184,652 lượt xem 14,198 lượt làm bài
Xem trước nội dung:
Cho hàm số xác định và có đạo hàm trên Khẳng định nào sau đây là sai?
Nếu hàm số đồng biến trên khoảng K thì
Nếu thì hàm số đồng biến trên K.
Nếu thì hàm số đồng biến trên K.
Cho hàm số xác định trên , với bất kỳ thuộc . Khẳng định nào sau đây là đúng?
Hàm số đồng biến trên khi và chỉ khi .
Hàm số nghịch biến trên khi và chỉ khi .
Hàm số đồng biến trên khi và chỉ khi .
Hàm số đồng biến trên khi và chỉ khi với mọi và .
Hàm số đồng biến trên khi và chỉ khi .
Nếu hàm số đồng biến trên thì đồ thị của nó đi lên từ trái sang phải trên .
Cho hàm số có đạo hàm trên .Khẳng định nào sau đây là sai?
Nếu thì hàm số đồng biến trên khoảng .
Hàm số nghịch biến trên khoảng khi và chỉ khi và chỉ tại một hữu hạn điểm .
Nếu hàm số đồng biến trên khoảng thì .
Hàm số nghịch biến trên khoảng khi và chỉ khi với mọi và
Nếu hàm số đồng biến trên , hàm số nghịch biến trên thì hàm số đồng biến trên .
Nếu hàm số đồng biến trên , hàm số nghịch biến trên và đều nhận giá trị dương trên thì hàm số đồng biến trên .
Nếu các hàm số , đồng biến trên thì hàm số đồng biến trên .
Khẳng định nào sau đây là sai?
Nếu hàm số đồng biến trên thì hàm số nghịch biến trên
Nếu hàm số đồng biến trên thì hàm số nghịch biến trên
Nếu hàm số đồng biến trên thì hàm số đồng biến trên
Nếu hàm số đồng biến trên khoảng thì hàm số đồng biến trên khoảng nào trong các khoảng sau đây?
A. .
Nếu hàm số đồng biến trên khoảng thì hàm số đồng biến trên khoảng nào?
A. .
A. Hàm số đồng biến trên .
B. Hàm số nghịch biến trên .
C. Hàm số nghịch biến trên .
B. Hàm số đã cho nghịch biến trên .
C. Hàm số đã cho đồng biến trên và nghịch biến trên .
Hàm số nghịch biến trên khoảng nào được cho dưới đây?
A. .
B. hoặc .
Hàm số nào sau đây nghịch biến trên toàn trục số?
A. .
B. .
Cho hàm số . Mệnh đề nào sau đây sai?
B. Hàm số đã cho đồng biến trên các khoảng và .
C. Trên các khoảng và , nên hàm số đã cho nghịch biến.
A.
Các khoảng nghịch biến của hàm số là:
Cho hàm số . Mệnh đề nào sau đây đúng?
Cho hàm số . Mệnh đề nào sau đây đúng?
Hàm số đã cho đồng biến trên R
Hàm số đã cho đồng biến trên
Hàm số đã cho đồng biến trên
Cho hàm số . Khẳng định nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên
C. Hàm số đã cho nghịch biến trên
Cho hàm số . Mệnh đề nào sau đây là đúng?
Hàm số đã cho nghịch biến trên
Hàm số đã cho nghịch biến trên
Hàm số đã cho nghịch biến trên
Hàm số nào sau đây đồng biến trên ?
Hàm số nào sau đây đồng biến trên R?
Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên .
B. Hàm số nghịch biến trên .
C. Hàm số đồng biến trên mỗi khoảng xác định.
Cho hàm số liên tục trên và có bảng biến thiên như sau:
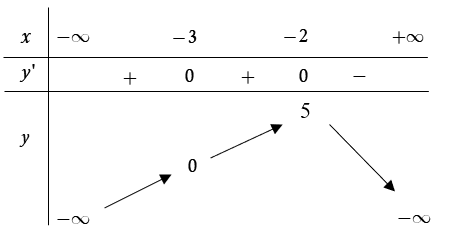
Trong các mệnh đề sau, có bao nhiêu mệnh đề sai?
I. Hàm số đã cho đồng biến trên các khoảng và .
II. Hàm số đã cho đồng biến trên khoảng .
III. Hàm số đã cho nghịch biến trên khoảng .
IV. Hàm số đã cho đồng biến trên khoảng .
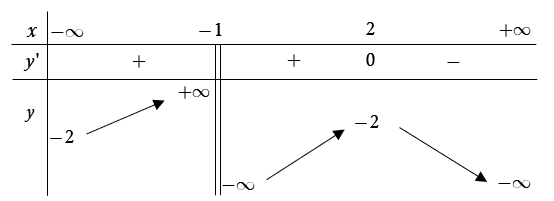
Hàm số đã cho đồng biến trên các khoảng và
Hàm số đã cho đồng biến trên
Hàm số đã cho đồng biến trên khoảng
Cho hàm số có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
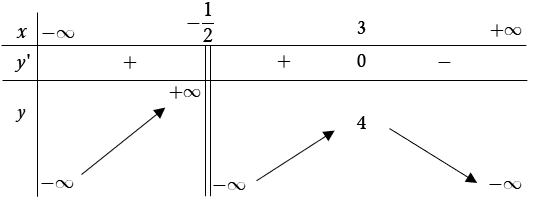
Hàm số đã cho đồng biến trên các khoảng và
Hàm số đã cho đồng biến trên khoảng
Hàm số đã cho nghịch biến trên khoảng
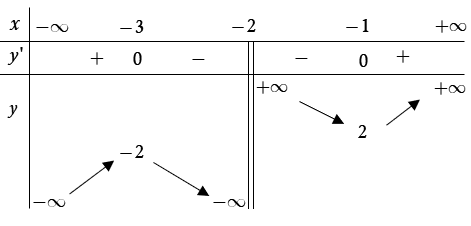
Khẳng định nào sau đây là đúng?
Hàm số đã cho nghịch biến trên khoảng
Hàm số đã cho đồng biến trên khoảng và
Cho hàm số xác định, liên tục trên và có đồ thị như hình vẽ bên. Khẳng định nào sau đây là sai?
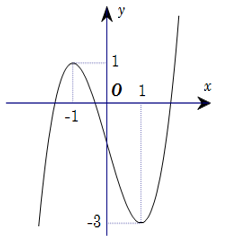
Hàm số đồng biến trên
Hàm số đồng biến trên và
Hàm số nghịch biến trên khoảng
Cho hàm số liên tục trên và có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?
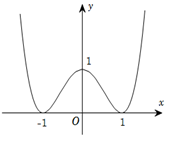
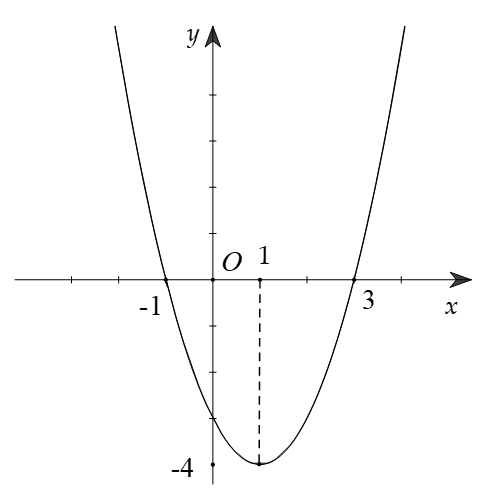
Hàm số đồng biến trên
Hàm số đồng biến trên và
Hàm số nghịch biến trên
Cho hàm số và hai số thực a,b sao cho a<b Khẳng định nào sau đây là đúng?
Cho hàm số và hai số thực sao cho u>v
Khẳng định nào sau đây là đúng?
Không so sánh và được.
Cho hàm số có đạo hàm trên sao cho Biết . Hỏi mệnh đề nào dưới đây đúng?
Hàm số đồng biến trên R khi:
Tìm tất các các giá trị thực của tham số m để hàm số đồng biến trên tập xác định.
Cho hàm số . Tìm giá trị lớn nhất của tham số thực m để hàm số đã cho đồng biến trên R .
Cho hàm số với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng
Cho hàm số . Tìm giá trị nhỏ nhất của tham số m để hàm số đồng biến trên R .
Cho hàm số . Tìm tất cả các giá trị của tham số thực m để hàm số nghịch biến trên R
Cho hàm số . Tìm tất cả các giá trị thực của tham số để hàm số đã cho đồng biến trên
Có bao nhiêu giá trị nguyên của tham số thực m thuộc khoảng để hàm số đồng biến trên khoảng ?
Tìm tất cả các giá trị của m để hàm số nghịch biến trên đoạn
Cho hàm số . Tìm tất cả các giá trị thực của tham số m để hàm số đã cho đồng biến trên khoảng
Tìm tất cả các giá trị thực của tham số m để hàm số giảm trên đoạn có độ dài lớn nhất bằng 1 .
Cho hàm số với m là tham số thực. Tìm tất cả các giá trị m để hàm số đồng biến trên khoảng
Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên và đồng biến trên .
Cho hàm số . Hỏi có bao nhiêu giá trị nguyên của tham số m để hàm số đồng biến trên khoảng
Cho hàm số với m là tham số thực. Gọi là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S .
Gọi là tập hợp các số nguyên m để hàm số đồng biến trên khoảng . Tính tổng T của các phần tử trong S
Tập tất cả các giá trị của tham số m để hàm số nghịch biến trên từng khoảng xác định là khoảng . Tính P=b-a .
Gọi S là tập hợp các số nguyên m để hàm số nghịch biến trên khoảng .Tính tổng T của các phần tử trong S
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng .
Tìm tất cả các giá trị thực của m để hàm số nghịch biến trên khoảng .
Tìm tất cả các giá trị thực của tham số m để hàm số nghịch biến trên khoảng
Tìm tất các các giá trị thực của tham số m để hàm số nghịch biến trên các khoảng xác định.
Tìm tất cả các giá trị của b để hàm số nghịch biến trên toàn trục số.
Cho hàm số có đạo hàm xác định, liên tục trên và có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?
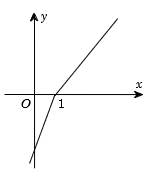
Hàm số đồng biến trên
Hàm số đồng biến trên và
Hàm số đồng biến trên
Cho hàm số . Biết rằng hàm số có đạo hàm là và hàm số có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai?
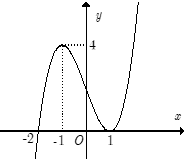
Trên thì hàm số luôn tăng.
Hàm giảm trên đoạn .
Hàm đồng biến trên khoảng .
Hàm số đã cho đồng biến trên khoảng
Hàm số đã cho nghịch biến trên các khoảng và
Hàm số đã cho đồng biến trên các khoảng và
Đề thi tương tự
1 mã đề 22 câu hỏi 1 giờ
183,600 xem14,114 thi
2 mã đề 95 câu hỏi 1 giờ
176,613 xem13,580 thi
7 mã đề 175 câu hỏi 1 giờ
179,821 xem13,827 thi
10 mã đề 238 câu hỏi 1 giờ
148,243 xem11,397 thi
1 mã đề 178 câu hỏi 1 giờ
152,840 xem11,752 thi
3 mã đề 55 câu hỏi 1 giờ
189,819 xem14,587 thi
1 mã đề 109 câu hỏi 1 giờ
185,762 xem14,280 thi
1 mã đề 194 câu hỏi 1 giờ
183,254 xem14,089 thi
