Trang chủ Đề thi Lớp 12 Toán Trắc nghiệm Toán 12 Bài 2: Mặt cầu có đáp án (Mới nhất)
thumbnail

Trắc nghiệm Toán 12 Bài 2: Mặt cầu có đáp án (Mới nhất)

Chương 2: Mặt nón, mặt trụ, mặt cầu
Bài 2 : Mặt cầu
Lớp 12;Toán

Thời gian làm bài: 1 giờ


Bạn chưa làm đề thi này!!!

Hãy bắt đầu chinh phục nào!



 

Xem trước nội dung:

Câu 1: 1 điểm

Cho đường tròn (C) đường kính AB và đường thẳng Δ . Để hình tròn xoay sinh bởi (C) khi quay quanh Δ là một mặt cầu thì cần có thêm điều kiện nào sau đây:

(I) Đường kính AB thuộc Δ .

(II) Δ cố định và đường kính AB thuộc Δ .

(III) Δ cố định và hai điểm A, B cố định trên Δ .

A.  
Chỉ (I).
B.  
Chỉ (II).
C.  
Chỉ (III).
D.  
Không cần thêm điều kiện nào.
Câu 2: 1 điểm
Cho mặt cầu (S) tâm O, bán kính R và mặt phẳng (P) có khoảng cách đến O bằng R. Một điểm M tùy ý thuộc (S). Đường thẳng OM cắt (P) tại N. Hình chiếu của O trên (P) là I. Mệnh đề nào sau đây đúng?
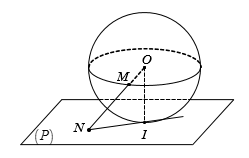
Hình ảnh
A.  
A. NI tiếp xúc với (S)
B.  
B.  O N = R 2 ⇔ I N = R .
C.  
Cả A và B đều sai.
D.  
Cả A và B đều đúng.
Câu 3: 1 điểm

Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một tiếp tuyến tiếp xúc với (S) tại B. Khi đó độ dài đoạn AB bằng:

A.  
R
B.  
R 2
C.  
R 2
D.  
R 3
Câu 4: 1 điểm
Cho mặt cầu S(O;R) và một điểm A, biết OA = 2R. Qua A kẻ một cát tuyến cắt (S) tại B và C sao cho B C = R 3 . Khi đó khoảng cách từ O đến BC bằng:
A.  
R
B.  
R 2
C.  
R 2
D.  
R 3
Câu 5: 1 điểm
Cho mặt cầu S(O;R) và mặt phẳng α . Biết khoảng cách từ O đến α bằng R 2 . Khi đó thiết diện tạo bởi mặt phẳng α với S(O;R) là một đường tròn có đường kính bằng:
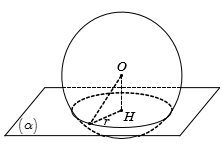
Hình ảnh
A.  
R
B.  
R 3
C.  
R 2
D.  
R 3 2
Câu 6: 1 điểm
Cho mặt cầu tâm I bán kính R = 2,6 cm. Một mặt phẳng cắt mặt cầu và cách tâm I một khoảng bằng 2,4 cm. Thế thì bán kính của đường tròn do mặt phẳng cắt mặt cầu tạo nên là:
A.  
1,2 cm
B.  
1,3 cm
C.  
1 cm
D.  
1,4 cm
Câu 7: 1 điểm
Diện tích hình tròn lớn của một hình cầu là p . Một mặt phẳng α cắt hình cầu theo một hình tròn có diện tích là p 2 . Khoảng cách từ tâm mặt cầu đến mặt phẳng α bằng:
A.  
p π
B.  
1 π
C.  
2 p π
D.  
p 2 π
Câu 8: 1 điểm
Một hình cầu có bán kính là 2m, một mặt phẳng cắt hình cầu theo một hình tròn có độ dài là 2 , 4 π m . Khoảng cách từ tâm mặt cầu đến mặt phẳng là:
A.  
1,6m
B.  
1,5m
C.  
1,4m
D.  
1,7m
Câu 9: 1 điểm

Cho mặt cầu S(O;R), A là một điểm ở trên mặt cầu (S) và (P) là mặt phẳng qua A sao cho góc giữa OA và (P) bằng 60o. Diện tích của đường tròn giao tuyến bằng:

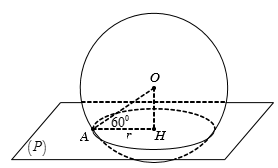
Hình ảnh

A.  
π R 2 .
B.  
π R 2 2 .
C.  
π R 2 4 .
D.  
π R 2 8 .
Câu 10: 1 điểm
Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng cạnh đáy bằng a. Khi đó mặt cầu nội tiếp hình chóp S.ABCD có bán kính bằng:
A.  
a 1 + 3 2 .
B.  
a 6 − 2 4 .
C.  
a 6 + 2 4 .
D.  
a 3 − 1 2 .
Câu 11: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và BA = BC = a. Cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:

A.  
a 2 2 .
B.  
3 a .
C.  
a 6 2 .
D.  
a 6 .
Câu 12: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên S A = a 6 và vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD ta được:

A.  
a 2 2 .
B.  
8 π a 2 .
C.  
2 a 2 .
D.  
2 π a 2 .
Câu 13: 1 điểm
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a. Cạnh bên S A = a 2 , hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:
A.  
a 2 2 .
B.  
a 6 3 .
C.  
a 6 2 .
D.  
a 2 3 .
Câu 14: 1 điểm

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng a 21 6 . Gọi h là chiều cao của khối chóp và R là bán kính mặt cầu ngoại tiếp khối chóp. Tỉ số R h bằng:

A.  
7 12
B.  
7 24 .
C.  
7 6 .
D.  
1 2 .
Câu 15: 1 điểm
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc 60o . Thể tích của khối cầu ngoại tiếp khối chóp S.ABCD là:
A.  
4 π a 3 3 .
B.  
2 π a 3 6 9 .
C.  
8 π a 3 6 9 .
D.  
8 π a 3 6 27 .
Câu 16: 1 điểm
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, đáy lớn AD = 2a, AB = BC = CD = a. Cạnh bên SA = 2a và vuông góc với đáy. Gọi R là bán kính mặt cầu ngoại tiếp khối chóp S.ABCD. Tỉ số R a nhận giá trị nào sau đây?
A.  
a 2 .
B.  
a
C.  
1
D.  
2 .
Câu 17: 1 điểm
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a, AD = a. Cạnh bên SA vuông góc với đáy và góc giữa SC với đáy bằng 45o. Gọi N là trung điểm SA, h là chiều cao của khối chóp S.ABCD và R là bán kính mặt cầu ngoại tiếp khối chóp N.ABC. Biểu thức liên hệ giữa R và h là:
A.  
4 R = 5 h .
B.  
5 R = 4 h .
C.  
R = 4 5 5 h .
D.  
R = 5 5 4 h .
Câu 18: 1 điểm
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Đường thẳng S A = a 2 vuông góc với đáy (ABCD). Gọi M là trung điểm SC, mặt phẳng α đi qua hai điểm A và M đồng thời song song với BD cắt SB, SD lần lượt tại E, F. Bán kính mặt cầu đi qua năm điểm S, A, E, M, F nhận giá trị nào sau đây?
A.  
a 2 .
B.  
a
C.  
a 2 2 .
D.  
a 2 .
Câu 19: 1 điểm
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc đáy (ABCD). Gọi H là hình chiếu của A trên đường thẳng SB. Bán kính mặt cầu ngoại tiếp tứ diện HBCD có giá trị nào sau đây?
A.  
a 2 .
B.  
a
C.  
a 2 2 .
D.  
a 2 .
Câu 20: 1 điểm
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và BC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên cạnh bên SB và SC. Thể tích của khối cầu tạo bởi mặt cầu ngoại tiếp hình chóp A.HKCB là:
A.  
2 π a 3 3 .
B.  
2 π a 3 .
C.  
π a 3 6 .
D.  
π a 3 2 .
Câu 21: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, BD = a. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy (ABCD) là trung điểm OD. Đường thẳng SD tạo với mặt đáy một góc bằng 60o. Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD nhận giá trị nào sau đây?

A.  
a 4 .
B.  
a 3 .
C.  
a 2 .
D.  
a
Câu 22: 1 điểm
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABC) là trung điểm H của cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC) bằng 60o . Gọi G  là trọng tâm tam giác SAC , R  là bán kính mặt cầu có tâm G  và tiếp xúc với mặt phẳng (SAB) . Đẳng thức nào sau đây sai?
A.  
R = d G , S A B .
B.  
3 13 R = 2 S H .
C.  
R 2 S Δ A B C = 4 3 39 .
D.  
R a = 13 .
Câu 23: 1 điểm
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối cầu ngoại tiếp hình chóp S.ABCD là:
A.  
2 π a 3 3 .
B.  
11 11 π a 3 162 .
C.  
π a 3 6 .
D.  
π a 3 3 .
Câu 24: 1 điểm

Cho hình chóp S.ABC có đáy ABC là một tam giác đều cạnh bằng a. Cạnh bên S A = a 3 và vuông góc với đáy (ABC). Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:

A.  
a 2 .
B.  
a 13 2 .
C.  
a 39 6 .
D.  
a 15 4 .
Câu 25: 1 điểm

Cho tứ diện O.ABC có các cạnh OA, OB, OC đôi một vuông góc và OA = a, OB = 2a, OC = 3a. Bán kính mặt cầu ngoại tiếp tứ diện O.ABC là:

A.  
a 3
B.  
3 a 2 .
C.  
a 6 2 .
D.  
a 14 2 .
Câu 26: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = AC = a. Cạnh bên SA vuông góc với đáy (ABC). Gọi I là trung điểm của BC, SI tạo với đáy (ABC) một góc 60o. Gọi S, V lần lượt là diện tích mặt cầu và thể tích khối cầu ngoại tiếp hình chóp S.ABC. Tỉ số V S bằng ?

A.  
a 14
B.  
a 14 12 .
C.  
3 a 14 4 .
D.  
a 2 6 .
Câu 27: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc B A D ^ = 120 0 . Cạnh bên S A = a 3 và vuông góc với đáy (ABCD). Bán kính mặt cầu ngoại tiếp khối chóp S.ACD nhận giá trị:

A.  
a 13 2 3 .
B.  
2 a 3 .
C.  
a 13 3 .
D.  
a 13 3 3 .
Câu 28: 1 điểm
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C và BC = a. Mặt phẳng (SAB) vuông góc với đáy, SA = SB = a, A S B ^ = 120 0 . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
A.  
a 4 .
B.  
a 2 .
C.  
a
D.  
2a
Câu 29: 1 điểm

Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, A C = a 3 , A C B ^   = 30 ∘ . Góc giữa đường thẳng AB' và mặt phẳng (ABC) bằng 60o. Bán kính mặt cầu ngoại tiếp tứ diện A'.ABC bằng:

A.  
3 a 4 .
B.  
a 21 4 .
C.  
a 21 2 .
D.  
a 21 8 .
Câu 30: 1 điểm

Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt đáy góc 60ovà điểm G là trọng tâm tam giác ABC. Bán kính mặt cầu ngoại tiếp khối chóp G.A'B'C' bằng:

A.  
85 a 108 .
B.  
3 a 2
C.  
3 a 4 .
D.  
31 a 36 .
Câu 31: 1 điểm
Người ta định nghĩa mặt cầu (S) như sau, hãy chọn câu trả lời đúng.
A.  
S = { M x , y , z / M I = R ;    I a , b , c và R ∈ R + 0 }
B.  
S = { M x , y , x / A M B ^ = 90 0 ;     A x A , y A , z A và B x B , y B , z B }
C.  
Mặt cầu (S) là mặt sinh ra bởi một đường tròn khi quay quanh một đường kính.
D.  
Ba câu A, B và C
Câu 32: 1 điểm
Phương trình mặt câu tâm  I(a, b,c ) có bán kính R là:
A.  
x 2 + y 2 + z 2 + 2 a x + 2 b y + 2 c z − R 2 = 0
B.  
x 2 + y 2 + z 2 + 2 a x + 2 b y + 2 c z + d = 0
C.  
x 2 + y 2 + z 2 + 2 a x + 2 b y + 2 c z + d = 0 ,     d = a 2 + b 2 + c 2 − R 2
D.  
x 2 + y 2 + z 2 − 2 a x − 2 b y − 2 c z + d = 0 ,    a 2 + b 2 + c 2 − d > 0
Câu 33: 1 điểm

S : x 2 + y 2 + z 2 − 2 a x − 2 b y − 2 c z + d = 0 là phương trình của mặt cầu khi và chỉ khi:

A.  
d ≠ 0
B.  
d < 0
C.  
d > 0
D.  
d ≠ a 2 + b 2 + c 2
Câu 34: 1 điểm

Điều kiện để S : x 2 + y 2 + z 2 + A x + B y + C z + D = 0 là một mặt cầu là:

A.  
A 2 + B 2 + C 2 − D > 0
B.  
A 2 + B 2 + C 2 − 2 D = 0
C.  
A 2 + B 2 + C 2 − 4 D > 0
D.  
A 2 + B 2 + C 2 + D = 0
Câu 35: 1 điểm

Cho hai mặt cầu (S) và (S’) lần lượt có tâm I và J, bán kính R và R’. Đặt d = IJ. Câu nào sau đây sai?

I. d > R − R ' ⇒ S và (S') trong nhau

II. 0 < d < R + R ' ⇒ S và (S') ngoài nhau

III. d = R − R ' ⇒ S và (S') tiếp xúc ngoài

IV. d = R + R ' ⇒ S và (S') tiếp xúc trong
A.  
Chỉ I và II
B.  
Chỉ I và III
C.  
Chỉ I và IV
D.  
Tất cả đều sai.
Câu 36: 1 điểm
Hai mặt cầu S : x 2 + y 2 + z 2 − 2 a x − 2 b y − 2 c z + d = 0 và S : x 2 + y 2 + z 2 − 2 a ' x − 2 b ' y − 2 c ' z + d ' = 0 , cắt nhau theo đường tròn có phương trình :
A.  
x 2 + y 2 + z 2 − 2 a x − 2 b y − 2 c z + d = 0 2 a − a ' x + 2 b − b ' y + 2 c − c ' z + d ' − d = 0
B.  
x 2 + y 2 + z 2 − 2 a ' x − 2 b ' y − 2 c ' z + d ' = 0 2 a − a ' x + 2 b − b ' y + 2 c − c ' z + d ' − d = 0
C.  
x 2 + y 2 + z 2 − 2 a x − 2 b y − 2 c z + d = 0 2 a − a ' x + 2 b − b ' y + 2 c − c ' z + d − d ' = 0
D.  
Hai câu A và B
Câu 37: 1 điểm

Cho mặt cầu S : x 2 + y 2 + z 2 − 2 a x − 2 b y − 2 c z + d = 0 và mặt phẳng P : A x + B y + C z + D = 0

I. A a + B b + C c + D − A 2 + B 2 + C 2 a 2 + b 2 + c 2 − d A 2 + B 2 + C 2 > 0 ⇒ P cắt (S)

II. A a + B b + C c + D − A 2 + B 2 + C 2 a 2 + b 2 + c 2 − d A 2 + B 2 + C 2 = 0 ⇒ P tiếp xúc (S)

III. A a + B b + C c + D − A 2 + B 2 + C 2 a 2 + b 2 + c 2 − d A 2 + B 2 + C 2 < 0 ⇒ P không cắt (S)
A.  
Chỉ I và II
B.  
Chỉ I và III
C.  
Chỉ II
D.  
Chỉ II
Câu 38: 1 điểm
Trong không gian với hệ trục tọa độ Oxyz cho 2 điểm A(1;3;0), B(-2;1;1) và đường thẳng: ( Δ ) :   x + 1 2 = y − 1 1 = z − 2 . Viết phương trình mặt cầu đi qua A, B và có tâm I thuộc  ( Δ )
A.  
x + 2 5 2 + y − 13 10 2 + z + 3 5 2 = 521 100
B.  
x + 2 5 2 + y − 13 10 2 + z + 3 5 2 = 25 3
C.  
x − 2 5 2 + y + 13 10 2 + z − 3 5 2 = 521 100
D.  
x + 2 5 2 + y − 13 10 2 + z + 3 5 2 = 25 3
Câu 39: 1 điểm

Với điều kiện nào của m thì mặt phẳng cong sau là mặt cầu? S : x 2 + y 2 + z 2 + 2 3 − m x − 3 m + 1 y − 2 m z + 2 m 2 + 7 = 0

A.  
m < 2 ∨    m > 3
B.  
1 ≤ m ≤ 3
C.  
m < 1   ∨   m < 3
D.  
m = 1   ∨    m = 3
Câu 40: 1 điểm
Giá trị α phải thỏa mãn điều kiện nào để mặt cong là mặt cầu: S : x 2 + y 2 + z 2 + 2 3 − cos 2 α x + 4 sin 2 α − 1 + 2 z + cos 4 α + 8 = 0 ?  k ∈ ℤ
A.  
2 π 3 + k 2 π < α < 4 π 3 + k 2 π
B.  
π 3 + k 2 π < α < 2 π 3 + k 2 π
C.  
− π 6 + k π < α < π 6 + k π
D.  
π 3 + k π < α < 2 π 3 + k π
Câu 41: 1 điểm

Giá trị t phải thỏa mãn điều kiện nào để mặt cong sau là mặt cầu: S : x 2 + y 2 + z 2 + 2 2 − ln t x + 4 ln t . y + 2 ln t + 1 z + 5 ln 2 t + 8 = 0

A.  
t < 1 e ∨ t > 3 e
B.  
1 e < t < 3 e
C.  
e < t < e 3
D.  
0 < t < 1 e ∨ t > e 3
Câu 42: 1 điểm

Tìm tập hợp các tâm I của mặt cầu S : x 2 + y 2 + z 2 + 2 1 − m x + 2 3 − 2 m y 2 m − 2 z + 5 m 2 − 9 m + 6 = 0

A.  
Đường thẳng: x + 1 = y + 3 2 = 2 − z
B.  
Phần đường thẳng: x + 1 = y + 3 2 = 2 − z với x < 0     ∨     x > 7
C.  
Phần đường thẳng: x + 1 = y + 3 2 = 2 − z với 0 < x < 7
D.  
Phần đường thẳng: x + 1 = y + 3 2 = z − 2 với x < 1     ∨     x > 8
Câu 43: 1 điểm
Với giá trị nào của m thì mặt phẳng P : 2 x − y + z − 5 = 0 tiếp xúc với mặt cầu  S : x 2 + y 2 + z 2 − 2 m x + 2 2 − m y − 4 m z + 5 m 2 + 1 = 0 ?
A.  
m = − 3
B.  
m = 1     ∨     m = − 3
C.  
m = 1
D.  
m = − 1     ∨     m = 3
Câu 44: 1 điểm

Với giá trị nào của m thì mặt phẳng Q : x + y + z + 3 = 0 cắt mặt cầu S : x 2 + y 2 + z 2 − 2 m + 1 x + 2 m y − 2 m z + 2 m 2 + 9 = 0 ?

A.  
− 4 < m < 5
B.  
m = − 4     ∨     m = 5
C.  
m > 5
D.  
m < − 4     ∨     m > 5
E.  
m < − 4
Câu 45: 1 điểm

Mặt phẳng P : 2 x − 4 y + 4 z + 5 = 0 và mặt cầu S : x 2 + y 2 + z 2 − 2 x + 4 y + 2 z − 3 = 0

A.  
Tiếp xúc
B.  
Không cắt nhau
C.  
Cắt nhau
D.  
(P) qua tâm của (S)
Câu 46: 1 điểm
Xét vị trí tương đối của mặt cầu S : x 2 + y 2 + z 2 − − 6 x − 4 y − 8 z + 13 = 0 và mặt phẳng  Q : x − 2 y + 2 z + 5 = 0.
A.  
Cắt nhau
B.  
Tiếp xúc
C.  
C (Q) là mặt phẳng đối xứng của (S)
D.  
D. Không cắt nhau
Câu 47: 1 điểm

Hai mặt cầu S : x 2 + y 2 + z 2 − 2 x − 6 y + 4 z + 5 = 0 ; S ' : x 2 + y 2 + z 2 − 6 x + 2 y − 4 z − 2 = 0 :

A.  
Tiếp xúc ngoài
B.  
Cắt nhau
C.  
Tiếp xúc ngoài
D.  
Cắt nhau.
Câu 48: 1 điểm
Hai mặt cầu  S : x 2 + y 2 + z 2 − 4 x + 6 y − 10 z − 11 = 0 ;   S ' : x 2 + y 2 + z 2 − 2 x + 2 y − 6 z − 5 = 0 :
A.  
Ngoài nhau
B.  
Cắt nhau
C.  
Tiếp xúc trong
D.  
Trong nhau
Câu 49: 1 điểm
Cho mặt cầu S : x 2 + y 2 + z 2 + 4 x − 2 y + 6 z − 2 = 0 và mặt phẳng P : 3 x + 2 y + 6 z + 1 = 0 . Gọi (C) là đường tròn giao tuyến của (P) và (S). Tính tọa độ tâm H của (C).
A.  
− 15 7 , 13 7 , − 3 7
B.  
15 7 , 13 7 , − 3 7
C.  
5 7 , 13 7 , − 3 7
D.  
15 7 , − 13 7 , 3 7
Câu 50: 1 điểm
Cho mặt cầu S : x 2 + y 2 + z 2 + 4 x − 2 y + 6 z − 2 = 0 và mặt phẳng P : 3 x + 2 y + 6 z + 1 = 0 . Gọi (C) là đường tròn giao tuyến của (P) và (S). Viết phương trình mặt cầu cầu (S') chứa (C) và điểm M(1,-2,1)
A.  
x 2 + y 2 + z 2 + 5 x − 8 y + 12 z − 5 = 0
B.  
x 2 + y 2 + z 2 − 5 x − 8 y + 12 z + 5 = 0
C.  
x 2 + y 2 + z 2 − 5 x + 8 y − 12 z + 5 = 0
D.  
x 2 + y 2 + z 2 − 5 x − 8 y − 12 z − 5 = 0
Câu 51: 1 điểm
Cho hai mặt cầu S : x 2 + y 2 + z 2 + 4 x − 2 y + 2 z − 3 = 0 và S ' : x 2 + y 2 + z 2 − 6 x + 4 y - 2 z − 2 = 0 ; Gọi (C) là giao tuyến của (S) và (S'). Viết phương trình của (C)
A.  
x 2 + y 2 + z 2 + 4 x − 2 y + 2 z − 3 = 0 10 x − 6 y + 4 z − 1 = 0
B.  
x 2 + y 2 + z 2 − 6 x + 4 y − 2 z − 2 = 0 10 x + 6 y − 4 z + 1 = 0
C.  
x 2 + y 2 + z 2 − 6 x + 4 y − 2 z − 2 = 0 10 x − 6 y + 4 z − 1 = 0
D.  
Hai câu A và C
Câu 52: 1 điểm
Cho hai mặt cầu S : x 2 + y 2 + z 2 + 4 x − 2 y + 2 z − 3 = 0 và S ' : x 2 + y 2 + z 2 − 6 x + 4 y - 2 z − 2 = 0. Gọi (C)  là giao tuyến của (S) và (S'). Viết phượng trình mặt cầu S 1 qua (C) và điểm A(2,1,-3)
A.  
x 2 + y 2 + z 2 + 26 x − 24 y + 2 z − 8 = 0
B.  
x 2 + y 2 + z 2 − 26 x + 24 y − 2 z + 8 = 0
C.  
x 2 + y 2 + z 2 − 106 x + 64 y − 42 z + 8 = 0
D.  
x 2 + y 2 + z 2 + 106 x − 64 y + 42 z − 8 = 0
Câu 53: 1 điểm

Cho mặt cầu S : x 2 + y 2 + z 2 − 6 x − 4 y − 4 z − 12 = 0 . Viết phương trình tổng quát của đường kính AB song song với đường thẳng D : x = 2 t + 1 ; y = 3 ; z = 5 t + 2 , t ∈ ℝ

A.  
5 x + 2 z − 11 = 0 y − 2 = 0
B.  
5 x − 2 z − 11 = 0 y − 2 = 0
C.  
5 x − 2 z + 11 = 0 y − 2 = 0
D.  
5 x + 2 z − 11 = 0 y − 2 = 0
Câu 54: 1 điểm
Cho mặt cầu S : x 2 + y 2 + z 2 − 6 x − 4 y − 4 z − 12 = 0 . Viết phương trình giao tuyến của (S) và mặt phẳng (yOz).
A.  
y − 2 2 + z − 2 2 = 20 x = 0
B.  
y − 2 2 + z − 2 2 = 4 x = 0
C.  
y + 2 2 + z + 2 2 = 4 x = 0
D.  
y + 2 2 + z + 2 2 = 20 x = 0
Câu 55: 1 điểm
Cho mặt cầu S : x 2 + y 2 + z 2 − 6 x − 4 y − 4 z − 12 = 0 . Viết phương trình tổng quát của mặt phẳng đối xứng (P) của (S) vuông góc với đường kính qua gốc O
A.  
3 x − 2 y + 2 z − 17 = 0
B.  
3 x + 2 y − 2 z + 17 = 0
C.  
2 x − 3 y − 2 z − 16 = 0
D.  
3 x + 2 y + 2 z − 17 = 0
Câu 56: 1 điểm

Cho mặt cầu S : x 2 + y 2 + z 2 − 6 x − 4 y − 4 z − 12 = 0 . Gọi A là giao điểm của (S) và trục y'Oy có tung độ âm. Viết phương trình tổng quát của tiếp diện (Q) của (S) tại A

A.  
3 x − 4 y + 2 z + 24 = 0
B.  
3 x + 4 y + 2 z − 8 = 0
C.  
3 x + 4 y + 2 z + 8 = 0
D.  
3 x − 4 y + 2 z − 24 = 0
Câu 57: 1 điểm
Viết phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD với A(0,-1,0); B(2,0,1); C(1,0,-1); D(1,-1,0)
A.  
x 2 + y 2 + z 2 − x + y − z − 2 = 0
B.  
x 2 + y 2 + z 2 − x − y − z − 2 = 0
C.  
x 2 + y 2 + z 2 − 2 x + y − 2 z + 2 = 0
D.  
x 2 + y 2 + z 2 + 2 x − 2 y + z + 2 = 0
Câu 58: 1 điểm
Với giá trị nào của m thì mặt cầu S : x 2 + y 2 + z 2 + 4 x − 2 m y + 4 m z + 4 m 2 + 3 m + 2 = 0 tiếp xúc trục z'Oz
A.  
-2
B.  
2
C.  
2 3
D.  
− 2 3
Câu 59: 1 điểm
Với giá trị nào của m thì hai mặt cầu sau tiếp xúc trong?
S : x − 3 2 + y + 2 2 + z + 1 2 = 81 ; S ' : x − 1 2 + y − 2 2 + z − 3 2 = m − 3 2 ,     m > 3
A.  
m = 6     ∨     m = 18
B.  
m = 12
C.  
m = 6
D.  
m = 18
Câu 60: 1 điểm
Tính bán kính của đường tròn giao tuyến của mặt phẳng P : x − 2 y + 2 z − 3 = 0 và mặt cầu S : x 2 + y 2 + z 2 − 4 x − 2 y + 6 z − 2 = 0
A.  
5
B.  
1
C.  
7
D.  
7
Câu 61: 1 điểm
Viết phương trình mặt cầu (S) tâm I(-2,1,-1) qua A(4,3,-2)
A.  
x 2 + y 2 + z 2 − 4 x + 2 y − 2 z + 35 = 0
B.  
x 2 + y 2 + z 2 + 4 x − 2 y + 2 z − 35 = 0
C.  
x 2 + y 2 + z 2 + 4 x − 2 y + 2 z + 35 = 0
D.  
x 2 + y 2 + z 2 + 4 x − 2 y − 2 z − 35 = 0
Câu 62: 1 điểm
Viết phương trình mặt cầu (S) tâm E(-1,2,4) qua gốc O
A.  
x 2 + y 2 + z 2 + 2 x − 4 y − 8 z + 42 = 0
B.  
x 2 + y 2 + z 2 + 2 x − 4 y − 8 z + 21 = 0
C.  
x 2 + y 2 + z 2 + 2 x − 4 y − 8 z − 42 = 0
D.  
x 2 + y 2 + z 2 + 2 x − 4 y − 8 z = 0
Câu 63: 1 điểm
Viết phương trình mặt cầu (S) đường kính AB với A(4,-3,5); B(2,1,3)
A.  
x 2 + y 2 + z 2 + 6 x + 2 y − 8 z − 26 = 0
B.  
x 2 + y 2 + z 2 − 6 x + 2 y − 8 z + 26 = 0
C.  
x 2 + y 2 + z 2 − 6 x + 2 y − 8 z + 20 = 0
D.  
x 2 + y 2 + z 2 + 6 x − 2 y + 8 z − 20 = 0
Câu 64: 1 điểm
Viết phương trình mặt cầu (S) tiếp xúc với hai mặt phẳng song song P : x − 2 y + 2 z + 6 = 0 ; Q : x − 2 y + 2 z − 10 = 0 và có tâm I ở trên trục y'Oy
A.  
x 2 + y 2 + z 2 − 2 y + 55 = 0
B.  
x 2 + y 2 + z 2 + 2 y − 60 = 0
C.  
x 2 + y 2 + z 2 + − 2 y − 55 9 = 0
D.  
x 2 + y 2 + z 2 + 2 y − 55 9 = 0
Câu 65: 1 điểm
Viết phương trình mặt cầu (S) tâm I(1,2,-3) tiếp xúc với mặt phẳng  P : 4 x − 2 y + 4 z − 3 = 0
A.  
x 2 + y 2 + z 2 − 2 x − 4 y + 6 z + 31 4 = 0
B.  
x 2 + y 2 + z 2 − 2 x − 4 y + 6 z + 31 = 0
C.  
x 2 + y 2 + z 2 − 2 x − 4 y + 6 z + 25 4 = 0
D.  
x 2 + y 2 + z 2 + − 2 x − 4 y + 6 z + 25 = 0
Câu 66: 1 điểm
Viết phương trình tổng quát của tiếp diện của mặt cầu S :    x 2 + y 2 + z 2 − 4 x − 2 y − 2 z − 10 = 0 song song với mặt phẳng  P :     2 x − 3 y + 6 z − 7 = 0
A.  
2 x − 3 y + 6 z − 17 = 0 ;    2 x − 3 y + 6 z + 24 = 0
B.  
2 x − 3 y + 6 z − 17 = 0 ;    2 x − 3 y + 6 z + 31 = 0
C.  
2 x − 3 y + 6 z + 21 = 0 ;    2 x − 3 y + 6 z − 35 = 0
D.  
2 x − 3 y + 6 z + 4 = 0 ;    2 x − 3 y + 6 z − 8 = 0
Câu 67: 1 điểm

Viết phươngng trình mặt cầu (S) tâm I(4,2,-1) nhận đường thẳng (D): x − 2 2 = y + 1 = z − 1 2 làm tiếp tuyến.

A.  
x − 4 2 + y − 2 2 + z + 1 2 = 4
B.  
x − 4 2 + y − 2 2 + z + 1 2 = 16
C.  
x − 4 2 + y − 2 2 + z + 1 2 = 9
D.  
x − 4 2 + y − 2 2 + z + 1 2 = 3
Câu 68: 1 điểm
Viết phương trình tiếp diện của mặt cầu S :    x 2 + y 2 + z 2 − 2 x − 2 y − 4 z − 2 = 0 qua trục y’Oy.
A.  
z = 0 ;     4 x − 3 z = 0
B.  
z = 0 ;     3 x − 4 z = 0
C.  
z = 0 ;     3 x + 4 z = 0
D.  
z = 0 ;     4 x + 3 z = 0
Câu 69: 1 điểm
Viết phương trình mặt cầu (S) tâm I(-3,2,2) tiếp xúc với mặt cầu (S’):
A.  
x + 3 2 + y − 2 2 + z − 2 2 = 100
B.  
x + 3 2 + y − 2 2 + z − 2 2 = 4
C.  
x + 3 2 + y − 2 2 + z − 2 2 = 2
D.  
x + 3 2 + y − 2 2 + z − 2 2 = 10
Câu 70: 1 điểm
Viết phương trình mặt cầu (S) qua gốc O và các giao điểm của mặt phẳng P :     2 x + y − 3 z + 6 = 0 với ba trục tọa độ 
A.  
x 2 + y 2 + z 2 − 3 x + 6 y + 2 z = 0
B.  
x 2 + y 2 + z 2 − 3 x − 6 y − 2 z = 0
C.  
x 2 + y 2 + z 2 + 3 x + 6 y + 2 z = 0
D.  
x 2 + y 2 + z 2 + 3 x + 6 y − 2 z = 0
Câu 71: 1 điểm
Cho mặt cầu S :    x 2 + y 2 + z 2 + 2 x − 2 y + 6 z − 5 = 0 và mặt phẳng P :   x − 2 y + 2 z + 3 = 0 . Gọi M là tiếp điểm của (S) và tiếp diện di động (Q) vuông góc với (P). tập hợp các điểm M là:
A.  
Mặt phẳng: x − 2 y + 2 z + 9 = 0
B.  
Mặt phẳng: x − 2 y + 2 z − 9 = 0
C.  
Đường tròn: x 2 + y 2 + z 2 + 2 x − 2 y + 6 z − 5 = 0 ;     x − 2 y + 2 z − 9 = 0
D.  
Đường tròn: x 2 + y 2 + z 2 + 2 x − 2 y + 6 z − 5 = 0 ;     x − 2 y + 2 z + 9 = 0
Câu 72: 1 điểm
Cho mặt cầu S :    x 2 + y 2 + z 2 + 2 x − 2 y + 6 z − 5 = 0 và mặt phẳng P :   x − 2 y + 2 z + 3 = 0 . Viết phương trình mặt cầu (S’) có bán kính nhỏ nhất chứa giao tuyến  của (S) và (P).
A.  
x 2 + y 2 + z 2 + 2 x + 2 y + 10 z − 27 = 0
B.  
x 2 + y 2 + z 2 + 2 x + 2 y + 10 z − 9 = 0
C.  
x 2 + y 2 + z 2 − 2 x 3 − 2 y 3 − 10 3 − 9 = 0
D.  
x 2 + y 2 + z 2 + 2 x 3 + 2 y 3 + 10 3 − 9 = 0
Câu 73: 1 điểm
Cho tứ diện ABCD có A(1,1,1); B(3,3,1); C(3,1,3); D(1,3,3). Viết phương trình mặt cầu ( S1 ) tiếp xúc với 6 cạnh của tứ diện
A.  
x − 2 2 + y − 2 2 + z − 2 2 = 4
B.  
x + 2 2 + y + 2 2 + z + 2 2 = 2
C.  
x − 2 2 + y − 2 2 + z − 2 2 = 1
D.  
x + 2 2 + y + 2 2 + z + 2 2 = 1
Câu 74: 1 điểm
Cho tứ diện ABCD có A(1,1,1); B(3,3,1; C(3,1,3); D(3,1,3). Viết phương trình mặt cầu ( S2 ) nội tiếp tứ diện.
A.  
x − 2 2 + y − 2 2 + z − 2 2 = 1 9
B.  
x − 2 2 + y − 2 2 + z − 2 2 = 1 3
C.  
x + 2 2 + y + 2 2 + z + 2 2 = 1 9
D.  
x + 2 2 + y + 2 2 + z + 2 2 = 1 3
Câu 75: 1 điểm
Viết phương trình mặt cầu ( S3 ) ngoại tiếp tứ diện.
A.  
x − 2 2 + y − 2 2 + z − 2 2 = 3
B.  
x − 2 2 + y − 2 2 + z − 2 2 = 9
C.  
x + 2 2 + y + 2 2 + z + 2 2 = 3
D.  
x + 2 2 + y + 2 2 + z + 2 2 = 9
Câu 76: 1 điểm

Viết phương trình mặt cầu (S) qua ba điểm A(2,0,1); B(1,3,2); C(3,2,0) có tâm nằm trong mặt phẳng (xOy)

A.  
x 2 + y 2 + z 2 + 6 x 5 + 17 y 5 − 13 5 = 0
B.  
x 2 + y 2 + z 2 − 6 x 5 + 17 y 5 + 13 5 = 0
C.  
x 2 + y 2 + z 2 − 6 x 5 − 17 y 5 − 13 5 = 0
D.  
x 2 + y 2 + z 2 + 6 x 5 − 17 y 5 + 13 5 = 0
Câu 77: 1 điểm
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có O A → ,    O C → ,    O G → trùng với ba trục O x → ,   O y → ,   O z → . Viết phương trình mặt cầu ( S1 ) ngoại tiếp hình lập phương.
A.  
x 2 + y 2 + z 2 − x − y − z − 3 2 = 0
B.  
x 2 + y 2 + z 2 + x + y + z = 0
C.  
x 2 + y 2 + z 2 + x + y + z − 3 2 = 0
D.  
x 2 + y 2 + z 2 − x − y − z = 0
Câu 78: 1 điểm
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có O A → ,    O C → ,    O G → trùng với ba trục O x → ,   O y → ,   O z → . Viết phương trình mặt cầu ( S2 ) nội tiếp hình lập phương.
A.  
x 2 + y 2 + z 2 + x + y + z + 1 = 0
B.  
x 2 + y 2 + z 2 − x − y − z + 1 2 = 0
C.  
x 2 + y 2 + z 2 − x − y − z + 1 = 0
D.  
x 2 + y 2 + z 2 + x + y + z − 1 2 = 0
Câu 79: 1 điểm

Cho hình lập phương QABC.DEFG có cạnh bằng 1 có O A → ,    O C → ,    O G → trùng với ba trục O x → ,   O y → ,   O z → . Viết phương trình mặt cầu ( S3) tiếp xúc với tất cả các cạnh của hình lập phương.

A.  
x 2 + y 2 + z 2 − x − y − z + 1 2 = 0
B.  
x 2 + y 2 + z 2 − x − y − z + 3 4 = 0
C.  
x 2 + y 2 + z 2 + x + y + z − 1 2 = 0
D.  
x 2 + y 2 + z 2 + x + y + z − 5 4 = 0
Câu 80: 1 điểm
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có O A → ,    O C → ,    O G → trùng với ba trục O x → ,   O y → ,   O z → . Sáu mặt phẳng x − y = 0 ;    y − z = 0 ;    z − x = 0 ;    x + y = 1 ;    y + z = 1 ;    z + x = 1 chia hình lập phương thành bao nhiêu phân bằng nhau?
A.  
10
B.  
8
C.  
4
D.  
6
Câu 81: 1 điểm

Cho hai điểm A(2,-3,-2); B(-4,5,-3). Tìm tập hợp các điểm M(x, y, z) sao cho A M B ^ = 90 o

A.  
Mặt cầu x 2 + y 2 + z 2 − 2 x + 2 y + 4 z + 20 = 0
B.  
Mặt cầu x 2 + y 2 + z 2 + 2 x − 2 y + 4 z − 20 = 0
C.  
Mặt cầu x 2 + y 2 + z 2 + 2 x − 2 y − 4 z + 20 = 0
D.  
Mặt cầu x 2 + y 2 + z 2 − 2 x − 2 y + 4 z − 20 = 0
Câu 82: 1 điểm

Cho hai điểm A(2,-3,-1); B(-4,5,-3). Tìm tập hợp các điểm M(x, y, z) thỏa mãn A M 2 + B M 2 = 124

A.  
Mặt cầu x 2 + y 2 + z 2 + 2 x + 2 y − 4 z + 30 = 0
B.  
Mặt phẳng 2 x − 2 x + 4 z − 30 = 0
C.  
Mặt cầu x 2 + y 2 + z 2 + 2 x − 2 y + 4 z − 30 = 0
D.  
Mặt cầu x 2 + y 2 + z 2 + 4 x − 4 y + 8 z + 60 = 0
Câu 83: 1 điểm

Cho hai điểm A(2,-3,-1); B()-4,5,-3. Tìm tập hợp các điểm M(x, y, z) thỏa mãn M A M B = 3 2

A.  
Mặt phẳng 20 x − 27 y + 5 z + 47 = 0
B.  
Mặt cầu x 2 + y 2 + z 2 − 20 x + 27 y + 5 z − 47 = 0
C.  
Mặt cầu x 2 + y 2 + z 2 + 40 x − 54 y + 10 z + 94 = 0
D.  
Mặt cầu x 2 + y 2 + z 2 − 40 x + 54 y − 10 z − 94 = 0
Câu 84: 1 điểm
Cho hai điểm A(2,-3,-1); B(-4,5,-3). Định k để tập hợp các điểm M(x, y, z) sao cho A M 2 + B M 2 = 2 k 2 + 1 ,    k ∈ ℝ + , là một mặt cầu.
A.  
0 < k < 5
B.  
k = 5
C.  
k > 5
D.  
5 < k < 21
Câu 85: 1 điểm

Cho ba điểm A(1,0,1); B(2,-1,0); C(0,-3,-1). Tìm tập hợp các điểm M(x, y, z) thỏa mãn A M 2 − B M 2 = C M 2

A.  
Mặt cầu x 2 + y 2 + z 2 − 2 x + 8 y + 4 z + 13 = 0
B.  
Mặt cầu x 2 + y 2 + z 2 − 2 x + 4 y + 8 z + 13 = 0
C.  
Mặt cầu x 2 + y 2 + z 2 + 2 x − 8 y − 4 z − 13 = 0
D.  
Mặt phẳng 2 x − 8 y − 4 z − 13 = 0
Câu 86: 1 điểm

Cho tứ diện OABC với A(-4,0,0); B(0,6,0); C(0,0,-8). Mặt cầu (S) ngoại tiếp từ diện có tâm và bán kính là:

A.  
I 2 , 3 , − 4 ,    R = 29
B.  
I − 2 , − 3 , 4 ,    R = 29
C.  
I − 2 , 3 , − 4 ,    R = 29
D.  
I − 2 , 3 , − 4 ,    R = 2 29
Câu 87: 1 điểm
Tìm tập hợp các tâm I của mặt cầu  S :   x 2 + y 2 + z 2 + 2 m − 2 x + 4 y − 2 z + 2 m + 4 = 0 ; m ∈ ℝ
A.  
Phần đường thẳng D : y + 2 = 0 ;    z − 1 = 0 − 3 < x < 1
B.  
Phần đường thẳng D : y + 2 = 0 ;    z − 1 = 0 < x − 3 ∨ x > 1
C.  
Mặt phẳng P : y + 2 = 0
D.  
Mặt phẳng Q :   z − 1 = 0
Câu 88: 1 điểm

Tìm tập hợp các tâm I của mặt cầu S :   x 2 + y 2 + z 2 + 2 3 − 4 cos t x − 2 4 sin t + 1 y − 4 z − 5 − 2 sin 2 t = 0 ,    t ∈ ℝ

A.  
Đường thẳng x + 3 4 = y − 1 4 = z − 2
B.  
Mặt phẳng z − 2 = 0
C.  
Đường tròn x − y + 4 = 0 với − 7 < x < 1 và − 3 < y < 5
D.  
Đường tròn x + 3 2 + y − 1 2 = 16 ;     z − 2 = 0
Câu 89: 1 điểm

Tìm tập hợp các tâm I của mặt cầu (S): x 2 + y 2 + z 2 − 6 cos t − 4 sin t y + 6 z cos 2 t − 3 = 0 , t ∈ ℝ

A.  
Mặt phẳng: 2 x + 3 y − 6 = 0
B.  
Mặt phẳng z + 3 = 0
C.  
Phần đường thẳng: 2 x + 3 y − 6 = 0 ;     z + 3 = 0 với − 3 ≤ x ≤ 3
D.  
Elip: x 2 9 + y 2 4 = 1 ;     z + 3 = 0
Câu 90: 1 điểm
Tìm tập hợp các tâm I của mặt cầu (S) có bán kinh thay đổi tiếp xúc với hai mặt phẳng  P :    2 x − y − 2 z + 1 = 0 ;     Q :   3 x + 2 y − 6 z + 5 = 0
A.  
Mặt phẳng: 5 x − 13 y + 4 z − 8 = 0
B.  
Hai mặt phẳng: 23 x − y − 32 z + 22 = 0 ; 5 x − 13 y + 4 z − 8 = 0
C.  
Hai phẳng: x − 2 y + 2 z + 1 = 0 ;     x − 2 y + 2 z + 1 = 0
D.  
Mặt phẳng: x − 2 y + 2 z − 5 = 0
Câu 91: 1 điểm

Tìm tập các tâm I của mặt cầu (S) tiếp xúc với hai mặt phẳng P :    x − 2 y + 2 z + 4 = 0 ;    Q : x − 2 y + 2 z − 6 = 0

A.  
Mặt phẳng: x − 2 y + 2 z − 1 = 0
B.  
Mặt phẳng: x − 2 y + 2 z − 2 = 0
C.  
Mặt phẳng: x − 2 y + 2 z + 1 = 0
D.  
Mặt phẳng: x − 2 y + 2 z − 5 = 0
Câu 92: 1 điểm
Tìm tập hợp các tâm I của mặt cầu (S) có bán kính R = 3 tiếp xúc với mặt phẳng  P :   4 x − 2 y − 4 z + 3 = 0
A.  
Hai mặt phẳng: 4 x − 2 y − 4 z + 6 = 0 ;     4 x − 2 y − 4 z = 0
B.  
Hai mặt phẳng: 4 x − 2 y − 4 z − 18 = 0 ;     4 x − 2 y − 4 z − 3 = 0
C.  
Hai mặt phẳng: 4 x − 2 y − 4 z − 15 = 0 ;     4 x − 2 y − 4 z + 21 = 0
D.  
hai mặt phẳng: 4 x − 2 y − 4 z + 15 = 0 ;     4 x − 2 y − 4 z − 21 = 0
Câu 93: 1 điểm
Tìm tập hợp các điểm M có cùng phương tích với hai mặt cầu  S 1 :    x 2 + y 2 + z 2 − 4 x + 6 y + 2 z − 5 = 0 ;  S 2 :    x 2 + y 2 + z 2 + 2 x − 8 y − 6 z + 3 = 0
A.  
Mặt phẳng: 3 x + 7 y − 4 z + 4 = 0
B.  
Mặt phẳng: 3 x − 7 y − 4 z + 4 = 0
C.  
Mặt phẳng: 3 x − 7 y + 4 z − 4 = 0
D.  
Mặt phẳng: 3 x − 7 y − 4 z − 8 = 0
Câu 94: 1 điểm
Cho mặt (S) tâm I ở trên z’Oz tiếp xúc với hai mặt phẳng P : 2 x − 2 y + z − 3 = 0 và Q :    x + 2 y − 2 z + 9 = 0 . Tính tọa độ tâm I và bán kính R:
A.  
I 0 , 0 , 4 ;     R = 1 3
B.  
I 0 , 0 , − 6 ;     R = 7
C.  
I 0 , 0 , 6 ;     R = 1
D.  
Hai câu A và C
Câu 95: 1 điểm
Cho hình hợp chữ nhật ABCD.EFGH có A(0,0,0); B(4,0,0); D(0;6;0); E(0,0,2). Tính diện tích mặt cầu (S) ngoại tiếp hình hợp chữ nhật.
A.  
28 π đvdt
B.  
42 π đvdt
C.  
152 π đvdt
D.  
56 π đvdt
E.  
Đáp số khác
Câu 96: 1 điểm
Cho hình hợp chữ nhật ABCD.EFGH có A(0,0,0); B(4,0,0); D(0,6,0); E(0,0,2). Ba mặt phẳng: x - 2z = 0; y - 3 = 0; x + 2z - 4 = 0 chia hình hộp chữ nhật thanh mấy phần bằng nhau?
A.  
10
B.  
8
C.  
6
D.  
4
Câu 97: 1 điểm
Cho tứ diện ABCD có A(1,2,3); B(0,0,3); C(0,2,0); D(1,0,0). Tìm tập hợp các điểm M thỏa mãn  A M → + B M → + C M → + D M → = 8
A.  
Mặt cầu: x − 1 2 2 + y − 1 2 + z − 3 2 2 = 4
B.  
Mặt cầu: x − 1 2 + y − 2 2 + z − 3 2 = 4
C.  
Mặt phẳng: x + 2 y + 3 z − 6 = 0
D.  
Mặt phẳng: 3 x + 2 y + z + 6 = 0
Câu 98: 1 điểm

Cho mặt cầu (S): x 2 + y 2 + z 2 − 4 x + 6 y + 2 z − 2 = 0 và điểm A(-6,-1,3). Gọi M là tiếp điểm của (S) và tiếp tuyến di động (d) qua A. Tìm tập hợp các điểm M.

A.  
Đường tròn: x 2 + y 2 + z 2 − 4 x + 6 y + 2 z − 2 = 0 ; 4 x − y − 2 z − 5 = 0
B.  
Đường tròn: x 2 + y 2 + z 2 + 4 x + 4 y − 2 z − 12 = 0 ; 4 x − y − 2 z − 5 = 0
C.  
Đường tròn: x 2 + y 2 + z 2 − 4 x + 6 y + 2 z − 2 = 0 ; 5 y − 7 = 0
D.  
Hai câu A và B
Câu 99: 1 điểm
Cho mặt cầu (S): x 2 + y 2 + z 2 − 4 x + 6 y + 2 z − 2 = 0 và điểm A(-6,-1,3). Gọi M là tiếp điểm của (S) và tiếp tuyến di động (d) qua A. Gọi (P) là tiếp điểm của (S) tại M và  là mặt phẳng qua M cắt hình cầu (S) theo hình trơn  có diện tích bằng 1 2 diện tích hình trơn lớn của (S). Tính góc tạo bởi (P) và (Q)
A.  
60 o
B.  
30 o
C.  
45 o
D.  
90 o
Câu 100: 1 điểm
Cho mặt cầu (S): x 2 + y 2 + z 2 − 4 x + 6 y + 2 z − 2 = 0 và điểm A(-6,-1,3). Gọi M là tiếp điểm của (S) và tiếp tuyến di động (d) qua A. Tính tọa độ giao điểm của AI và mặt cầu (S).
A.  
2 ± 16 21 21 ;    − 3 ± 4 21 21 ;    − 1 ± 8 21 21
B.  
2 ± 4 21 21 ;    − 3 ± 21 21 ;    − 1 ± 2 21 21
C.  
2 ± 8 21 21 ;    − 3 ∓ 2 21 21 ;    − 1 ∓ 4 21 21
D.  
2 ± 16 21 21 ;    − 3 ∓ 4 21 21 ;    − 1 ∓ 8 21 21
Câu 101: 1 điểm

Cho tứ diện ABCD có A(3, 6, -2); B(6, 0, 1); C(-1, 2, 0); D(0, 4, 1). Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ :

A.  
I(3, -2, 1)
B.  
(3, 2, -1)
C.  
I(-3, 2, 1)
D.  
I(3, -2, -1)
Câu 102: 1 điểm
Trong không gian Oxyz cho mặt cầu (S) có phương trình x 2 + y 2 + z 2 − x + y − 3 z + 7 4 = 0 , (S) có tọa độ tâm I và bán kính R là
A.  
I 1 2 , − 1 2 , 3 2 , R = 1 2 .
B.  
I 1 2 , − 1 2 , 3 2 , R = 1.
C.  
I 1 2 , 1 2 , − 3 2 , R = 1.
D.  
I 1 2 , 1 2 , 3 2 , R = 1.
Câu 103: 1 điểm

Trong không gian Oxyz cho đường tròn: C : x 2 + y 2 + z 2 − 4 x + 6 y + 6 z + 17 = 0 x − 2 y + 2 z + 1 = 0 . Tọa độ tâm H của (C) là:

A.  
H 5 3 , − 7 3 , − 11 3 .
B.  
H 5 3 , 7 3 , − 11 3 .
C.  
H 5 3 , − 7 3 , 11 3 .
D.  
H 5 3 , 7 3 , 11 3 .
Câu 104: 1 điểm

Trong không gian cho đường tròn C : x 2 + y 2 + z 2 − 4 x + 6 y + 6 z + 17 = 0 x − 2 y + 2 z + 1 = 0 . Bán kính r của đường tròn (C) bằng :

A.  
r = 6 2 .
B.  
r = 3 .
C.  
r = 2.
D.  
r = 3.
Câu 105: 1 điểm

Trong không gian Oxyz cho đường tròn C : x 2 + y 2 + z 2 − 2 x − 4 y − 6 z − 67 = 0 2 x − 2 y + z + 5 = 0 . Bán kính r của (C) bằng:

A.  
r = 6 2 .
B.  
r = 8.
C.  
r = 77 .
D.  
r = 78 .
Câu 106: 1 điểm
Trong không gian tọa độ Oxyz cho đường tròn C : x 2 + y 2 + z 2 − 12 x + 4 y − 6 z − 24 = 0 2 x + 2 y + z + 1 = 0 . Tâm H của (C) là điểm có tọa độ:
A.  
H 10 3 , 14 3 , 5 3 .
B.  
H 10 3 , − 14 3 , 5 3 .
C.  
H 10 3 , − 14 3 , − 5 3 .
D.  
H 10 3 , 14 3 , − 5 3 .
Câu 107: 1 điểm

Trong không gian Oxyz cho đường tròn ( C ) : x 2 + y 2 + z 2 − 4 = 0 x + z − 2 = 0 .Bán kính r của đường tròn (C) bằng :

A.  
r = 2.
B.  
r = 3 .
C.  
r = 5 .
D.  
r = 3.
Câu 108: 1 điểm

Trong không gian Oxyz cho đường tròn ( C ) : x 2 + y 2 + z 2 − 4 = 0 x + z − 2 = 0 (C) có tâm H và bán kính r bằng:

A.  
H 1 , 1 , 0 , r = 2 .
B.  
H 1 , 0 , 1 , r = 2 .
C.  
H 0 , 1 , 1 , r = 2 .
D.  
H 1 , 0 , − 1 , r = 2 .
Câu 109: 1 điểm

Cho mặt cầu S : x 2 + y 2 + z 2 − 2 x − 4 z − 4 = 0 và ba điểm A(1,2,-2); B(-4,2,3); C(1,-3,3) nằm trên mặt cầu (S). Bán kính r của đường tròn ngoại tiếp tam giác ABC là :

A.  
r = 3 .
B.  
r = 5 .
C.  
r = 6 .
D.  
r = 2 2 .

Xem thêm đề thi tương tự

thumbnail
Trắc nghiệm Toán 12 Bài 2: Cực trị của hàm số có đáp án (Mới nhất)Lớp 12Toán
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Bài 2: Cực trị của hàm số
Lớp 12;Toán

95 câu hỏi 2 mã đề 1 giờ

176,556 lượt xem 95,060 lượt làm bài

Chưa chinh phục!!!
thumbnail
Trắc nghiệm Bài tập Toán 4 Chương 2 Bài 12: Nhân với số có một chữ số có đáp ánLớp 4Toán
Trắc nghiệm tổng hợp Toán 4 có đáp án
Lớp 4;Toán

60 câu hỏi 3 mã đề 1 giờ

152,743 lượt xem 82,236 lượt làm bài

Chưa chinh phục!!!
thumbnail
Trắc nghiệm Toán 5 Bài 12 (có đáp án): Ôn tập: Bảng đơn vị đo độ dài (phần 2)Lớp 5Toán
Chương 1: Ôn tập và bổ sung về phân số. Giải toán liên quan đến tỉ lệ. Bảng đơn vị đo diện tích
Ôn tập bảng đơn vị đo độ dài
Lớp 5;Toán

6 câu hỏi 1 mã đề 1 giờ

188,786 lượt xem 101,640 lượt làm bài

Chưa chinh phục!!!
thumbnail
Trắc nghiệm Toán 12 Bài 4: Đường tiệm cận có đáp án (Mới nhất)Lớp 12Toán
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Bài 4: Đường tiệm cận
Lớp 12;Toán

55 câu hỏi 1 mã đề 1 giờ

189,655 lượt xem 102,109 lượt làm bài

Chưa chinh phục!!!
thumbnail
Trắc nghiệm Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số có đáp án (Mới nhất)Lớp 12Toán
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Bài 1: Sự đồng biến, nghịch biến của hàm số
Lớp 12;Toán

65 câu hỏi 1 mã đề 1 giờ

184,592 lượt xem 99,386 lượt làm bài

Chưa chinh phục!!!
thumbnail
Trắc nghiệm Toán 12 Bài Khái niệm về thể tích khối đa diện có đáp án (Mới nhất)Lớp 12Toán
Chương 1: Khối đa diện
Bài 3: Khái niệm về thể tích của khối đa diện
Lớp 12;Toán

80 câu hỏi 2 mã đề 1 giờ

180,111 lượt xem 96,971 lượt làm bài

Chưa chinh phục!!!
thumbnail
Trắc nghiệm Toán 12 Bài tập nguyên hàm có đáp án (Mới nhất)Lớp 12Toán
Chương 3: Nguyên hàm - Tích phân và ứng dụng
Bài 1 : Nguyên hàm
Lớp 12;Toán

102 câu hỏi 1 mã đề 1 giờ

154,824 lượt xem 83,349 lượt làm bài

Chưa chinh phục!!!
thumbnail
Trắc nghiệm Toán 12 Bài 3: Giá trị lớn nhất giá trị nhỏ nhất của hàm số có đáp án (Mới nhất)Lớp 12Toán
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Lớp 12;Toán

40 câu hỏi 1 mã đề 1 giờ

157,811 lượt xem 84,959 lượt làm bài

Chưa chinh phục!!!
thumbnail
Trắc nghiệm Toán 4 Bài 12: (có đáp án) biểu đồLớp 4Toán
Chương 1: Số tự nhiên. Bảng đơn vị đo khối lượng
Biểu đồ
Lớp 4;Toán

13 câu hỏi 1 mã đề 1 giờ

176,908 lượt xem 95,249 lượt làm bài

Chưa chinh phục!!!