
Trắc nghiệm Toán 12 Mũ và lôgarit có đáp án (Mới nhất)
Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit <br> Bài 4: Hàm số mũ. Hàm số lôgarit <br> Lớp 12;Toán <br>
Đề thi nằm trong bộ sưu tập: TOÁN 12
Số câu hỏi: 46 câuSố mã đề: 1 đềThời gian: 1 giờ
173,204 lượt xem 13,320 lượt làm bài
Xem trước nội dung:
Nghiệm của phương trình là
Tập nghiệm của bất phương trình là
Với a là số thực dương tùy ý, bằng
Nghiệm của phương trình là
Nghiệm của phương trình là
Với a,b là các số thực dương tùy ý thỏa mãn , mệnh đề nào dưới đây đúng?
Tập nghiệm của bất phương trình là
Nghiệm của phương trình là:
Nghiệm của phương trình là
Tập xác định của hàm số là
Với a,b là các số thực dương tùy ý và , bằng
Tập nghiệm của bất phương trình là
Cho a và b là hai số thực dương thỏa mãn . Giá trị của bằng
Nghiệm của phương trình là
Với a là số thực dương tùy ý, bằng
Tập nghiệm của bất phương trình là
Xét các số thực thỏa mãn . Mệnh đề nào là đúng?
Tập nghiệm của bất phương trình là
Xét tất cả các số dương a và b thỏa mãn . Mệnh đề nào dưới đây đúng?
Tập nghiệm của bất phương trình là
Cho x, y là các số thực dương thỏa mãn . Giá trị của bằng
Với a là số thực dương tùy,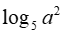 bằng
bằng
Cho hàm số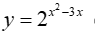 có đạo hàm là
có đạo hàm là
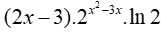
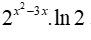
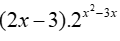
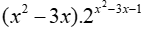
Cho a và b là hai số thực dương thỏa mãn
. Giá trị của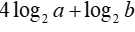 bằng
bằng
Nghiệm của phương trình 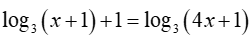 là
là
Phương trình có nghiệm là
Xét các số thực x,y thỏa mãn . Giá trị nhỏ nhất của biểu thức gần nhất với số nào dưới đây
Có bao nhiêu cặp số nguyên dương sao cho và ứng với mỗi cặp tồn tại đúng 3 số thực thỏa mãn ?
Xét các số thực x và y thỏa mãn . Giá trị lớn nhất của biểu thức gần nhất với số nào dưới đây?
Có bao nhiêu cặp số nguyên dương sao cho và ứng với mỗi cặp tồn tại đúng 3 số thực thỏa mãn ?
Xét các số thực dương thỏa mãn và . Giá trị nhỏ nhất của biểu thức thuộc tập hợp nào dưới đây?
Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn ?
Cho phương trình (m là tham số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn .
Có bao nhiêu cặp số nguyên thỏa mãn và ?
Cho phương trình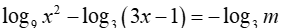 (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm
(m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm
Cho phương trình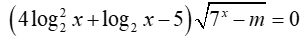 ( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt
( m là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử?
Cho , thỏa mãn . Giá trị của bằng
Cho phương trình với m là tham số. Có bao nhiêu giá trị nguyên của để phương trình đã cho có nghiệm?
Đề thi tương tự
1 mã đề 25 câu hỏi 1 giờ
160,763 xem12,357 thi
1 mã đề 20 câu hỏi 1 giờ
166,890 xem12,830 thi
1 mã đề 30 câu hỏi 1 giờ
168,507 xem12,951 thi
1 mã đề 20 câu hỏi 1 giờ
175,013 xem13,456 thi
8 mã đề 240 câu hỏi 1 giờ
170,301 xem13,085 thi
1 mã đề 10 câu hỏi 1 giờ
160,552 xem12,347 thi
2 mã đề 95 câu hỏi 1 giờ
176,613 xem13,580 thi
1 mã đề 14 câu hỏi 1 giờ
160,963 xem12,373 thi
1 mã đề 39 câu hỏi 1 giờ
160,353 xem12,330 thi
