Trang chủ Đề thi THPT Quốc gia Toán 13994
thumbnail

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 1: Hàm số và ứng dụng có đáp án

Bộ trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán, tập trung vào chủ đề Hàm số và ứng dụng. Tài liệu cung cấp các câu hỏi bám sát cấu trúc đề thi chính thức, kèm đáp án chi tiết, giúp học sinh rèn luyện và củng cố kiến thức một cách hiệu quả.

Từ khoá: Toán học hàm số ứng dụng hàm số ôn thi tốt nghiệp trắc nghiệm năm 2022 đề thi có đáp án

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết📘 Tuyển Tập Đề Thi Tham Khảo Các Môn THPT Quốc Gia 2025 🎯

Số câu hỏi: 170 câuSố mã đề: 10 đềThời gian: 1 giờ

182,051 lượt xem 13,994 lượt làm bài


Chọn mã đề:


Bạn chưa làm Đề số 7!!!

 

Xem trước nội dung:

Câu 1: 1 điểm

Một trong bốn đường thẳng dưới đây là đường tiệm cận ngang của đồ thị hàm số ở Hình 1. Hỏi đường tiệm cận ngang của đồ thị hàm số đó là đường nào?

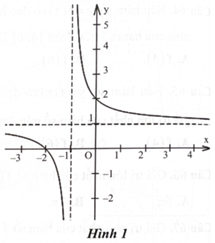
Hình ảnh
A.  
\(x = - 1.\)                         
B.  
\(x = - 2.\)                   
C.  
\({\rm{y}} = 1.\)           
D.  
\({\rm{y}} = 2.\)
Câu 2: 1 điểm

Một trong bốn đường thẳng dưới đây là đường tiệm cận đứng của đồ thị hàm số ở Hình 1. Hỏi đường tiệm cận đứng của đồ thị hàm số đó là đường nào?

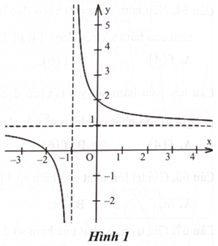
Hình ảnh
A.  
\({\rm{x}} = - 1.\)       
B.  
\({\rm{x}} = - 2.\)       
C.  
\({\rm{y}} = 1.\)           
D.  
\({\rm{y}} = 2.\)
Câu 3: 1 điểm

Một trong bốn đường thẳng dưới đây là đường tiệm cận xiên của đồ thị hàm số ở Hình 2. Hỏi đường tiệm cận xiên của đồ thị hàm số đó là đường nào?

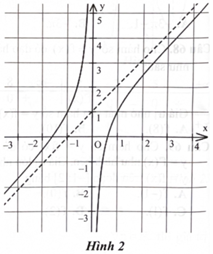
Hình ảnh
A.  
\(y = x.\)                       
B.  
\({\rm{y}} = {\rm{x}} + 1.\)                                 
C.  
\(y = - x + 1.\)                        
D.  
\(y = 2x + 1.\)
Câu 4: 1 điểm
Cho hàm số \(y = f(x)\) có \(\mathop {\lim }\limits_{x \to 3} f(x) = + \infty ,\mathop {\lim }\limits_{x \to - \infty } f(x) = - 3.\) Phát biểu nào sau đây là đúng? 
A.  
Đồ thị hàm số có tiệm cận ngang là đường thẳng \({\rm{y}} = 3\) và tiệm cận đứng là đường thẳng \({\rm{x}} = - 3.\)
B.  
Đồ thị hàm số có tiệm cận ngang là đường thẳng \(x = 3\) và tiệm cận đứng là đường thẳng \({\rm{y}} = - 3.\)
C.  
Đồ thị hàm số có tiệm cận ngang là đường thẳng \(x = - 3\) và tiệm cận đứng là đường thẳng \({\rm{y}} = 3.\)
D.  
Đồ thị hàm số có tiệm cận ngang là đường thẳng \({\rm{y}} = - 3\) và tiệm cận đứng là đường thẳng \({\rm{x}} = 3.\)
Câu 5: 1 điểm
Cho hàm số \(y = f(x)\) thoả mãn \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - 5x + 7] = 0.\) Đường tiệm cận xiên của đồ thị hàm số \(y = f(x)\) là 
A.  
\({\rm{y}} = 5{\rm{x}} - 7.\)
B.  
\({\rm{y}} = 5{\rm{x}} + 7.\)
C.  
\(y = - 5x - 7.\)
D.  
\(y = 5x + 7.\)
Câu 6: 1 điểm

Cho hàm số phù hợp với bảng biến thiên sau:

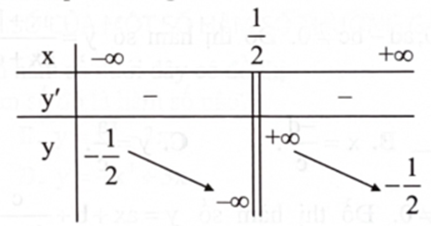
Hình ảnh

Phát biểu nào sau đây là đúng?

A.  
Đồ thị hàm số có đường tiệm cận ngang là \({\rm{y}} = \frac{{ - 1}}{2}\), đường tiệm cận đứng là \({\rm{x}} = \frac{1}{2}.\)
B.  
Đồ thị hàm số có đường tiệm cận ngang là \({\rm{y}} = \frac{1}{2}\), đường tiệm cận đứng là \(x = \frac{{ - 1}}{2}.\)
C.  
Đồ thị hàm số chỉ có đúng một đường tiệm cận, đó là \({\rm{y}} = \frac{{ - 1}}{2}.\)
D.  
Đồ thị hàm số chỉ có đúng một đường tiệm cận, đó là \(x = \frac{1}{2}.\)
Câu 7: 1 điểm

Cho hàm số phù hợp với bảng biến thiên sau:

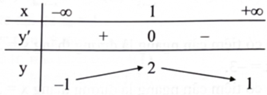
Hình ảnh

Phát biểu nào sau đây là đúng?

A.  
Đồ thị hàm số có hai đường tiệm cận ngang là \({\rm{y}} = - 1,{\rm{y}} = 1.\)
B.  
Đồ thị hàm số có hai đường tiệm cận ngang là \({\rm{x}} = - 1,{\rm{x}} = 1.\)
C.  
Đồ thị hàm số không có đường tiệm cận ngang.
D.  
Đồ thị hàm số có đường tiệm cận đứng.
Câu 8: 1 điểm
Cho \({\rm{ac}} e 0,{\rm{ad}} - {\rm{bc}} e 0.\) Đồ thị hàm số \({\rm{y}} = \frac{{{\rm{ax}} + {\rm{b}}}}{{{\rm{cx}} + {\rm{d}}}}\) có đường tiệm cận ngang là 
A.  
\({\rm{x}} = \frac{{\rm{a}}}{{\rm{c}}}.\)
B.  
\(x = \frac{{ - d}}{c}.\)
C.  
\({\rm{y}} = \frac{{\rm{a}}}{{\rm{c}}}.\)
D.  
\(y = \frac{{ - d}}{c}.\)
Câu 9: 1 điểm
Cho \({\rm{ac}} e 0,{\rm{ad}} - {\rm{bc}} e 0.\) Đồ thị hàm số \({\rm{y}} = \frac{{{\rm{ax}} + {\rm{b}}}}{{{\rm{cx}} + {\rm{d}}}}\) có đường tiệm cận đứng là 
A.  
\({\rm{x}} = \frac{{\rm{a}}}{{\rm{c}}}.\)
B.  
\(x = \frac{{ - d}}{c}.\)
C.  
\({\rm{y}} = \frac{{\rm{a}}}{{\rm{c}}}.\)
D.  
\({\rm{y}} = \frac{{ - {\rm{d}}}}{{\rm{c}}}.\)
Câu 10: 1 điểm
Cho \({\rm{acd}} e 0.\) Đồ thị hàm số \({\rm{y}} = {\rm{ax}} + {\rm{b}} + \frac{{\rm{c}}}{{{\rm{dx}} + {\rm{e}}}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}},{\rm{e}} \in \mathbb{R})\) có đường tiệm cận xiên là 
A.  
\(y = ax + b.\)
B.  
\(y = dx + e.\)
C.  
\(y = bx + a.\)
D.  
\(y = ex + d.\)
Câu 11: 1 điểm
Đồ thị hàm số \(y = \frac{{x - 1}}{{x + 1}}\) có: 
A.  
Tiệm cận ngang là đường thẳng \({\rm{y}} = 1\) và tiệm cận đứng là đường thẳng \({\rm{x}} = 1.\)
B.  
Tiệm cận ngang là đường thẳng \({\rm{y}} = 1\) và tiệm cận đứng là đường thẳng \(x = - 1.\)
C.  
Tiệm cận ngang là đường thẳng \({\rm{y}} = - 1\) và tiệm cận đứng là đường thẳng \({\rm{x}} = 1.\)
D.  
Tiệm cận ngang là đường thẳng \({\rm{y}} = - 1\) và tiệm cận đứng là đường thẳng \({\rm{x}} = - 1.\)
Câu 12: 1 điểm
Cho đường thẳng \({\rm{y}} = {\rm{ax}} + {\rm{b}}({\rm{a}},{\rm{b}} \in \mathbb{R})\) là đường tiệm cận xiên của đồ thị hàm số \({\rm{y}} = \frac{{ - 3{{\rm{x}}^2} + 5{\rm{x}} + 1}}{{2{\rm{x}} + 1}}.\) Giá trị của a là 
A.  
\(\frac{3}{2}.\)
B.  
\(\frac{{ - 3}}{2}.\)
C.  
\(\frac{2}{3}.\)
D.  
\(\frac{{ - 2}}{3}.\)
Câu 13: 1 điểm
Cho đường thẳng \({\rm{y}} = {\rm{ax}} + {\rm{b}}({\rm{a}},{\rm{b}} \in \mathbb{R})\) là đường tiệm cận xiên của đồ thị hàm số \({\rm{y}} = \sqrt {9{{\rm{x}}^2} + 1} .\) Tập hợp các giá trị của a là 
A.  
\(\{ 3\} .\)
B.  
\(\{ - 3\} .\)
C.  
\(\{ - 3;3\} .\)
D.  
\(\{ 9\} .\)
Câu 14: 1 điểm
Số đường tiệm cận đứng của đồ thị hàm số \({\rm{y}} = \frac{{\sin {\rm{x}}}}{{\rm{x}}}\) là 
A.  
0.
B.  
1.
C.  
2.
D.  
3.
Câu 15: 1 điểm
Số đường tiệm cận đứng của đồ thị hàm số \({\rm{y}} = \frac{{{{\rm{e}}^{\rm{x}}} - 1}}{{\rm{x}}}\) là
A.  
0.
B.  
1.
C.  
2.
D.  
3.

Đề thi tương tự

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 4: Thống kê và xác suất có đáp án

10 mã đề 149 câu hỏi 1 giờ

184,813 xem14,203 thi

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Hóa Bài 17. Nguyên tố nhóm IA có đáp án

1 mã đề 30 câu hỏi 1 giờ

337,656 xem25,960 thi

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Hóa Bài 8. Đại cương về Polymer có đáp án

1 mã đề 57 câu hỏi 1 giờ

292,236 xem22,472 thi

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 2: Nguyên hàm, tích phân và ứng dụng có đáp án

7 mã đề 113 câu hỏi 1 giờ

158,052 xem12,147 thi

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 6: Hình học và đo lường trong không gian có đáp án

6 mã đề 165 câu hỏi 1 giờ

177,465 xem13,642 thi

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Hóa Bài 15. Tách kim loại và tái chế kim loại có đáp án

1 mã đề 28 câu hỏi 1 giờ

291,765 xem22,430 thi

Trắc Nghiệm Tổng Hợp Ôn Thi Tốt Nghiệp THPT Môn Hóa - Bài 1: Ester, Lipid, Chất Béo - Miễn Phí, Có Đáp Án

1 mã đề 66 câu hỏi 1 giờ

305,936 xem23,526 thi

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Hóa Bài 9. Vật liệu polymer có đáp án

1 mã đề 20 câu hỏi 1 giờ

318,590 xem24,500 thi

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 7: Cấp số cộng - cấp số nhân có đáp án

4 mã đề 49 câu hỏi 1 giờ

160,573 xem12,344 thi

Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Hóa Bài 13. Cấu tạo và tính chất vật lí của kim loại có đáp án

1 mã đề 28 câu hỏi 1 giờ

305,945 xem23,526 thi