Trang chủ   Hỏi & đáp   THPT Quốc gia   Toán   Câu hỏi số #8705  

Cho các số thực x,yx , y thỏa mãn . Gọi M,mM , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P=11+xyP = \dfrac{1}{1 + x y}. Tính M−mM - m.

A.  

M−m=3M - m = 3.

B.  

M−m=1M - m = 1.

C.  

M−m=12M - m = \dfrac{1}{2}.

D.  

M−m=2M - m = 2.

Đáp án đúng là: B

Giải thích đáp án:

ex2+2y2+exy(x2−xy+y2−1)−e1+xy+y2=0⇔ex2+2y2−xy+(x2−xy+y2−1)−e1+y2=0⇔ex2+2y2−xy+(x2−xy+2y2)−(1+y2)−e1+y2=0⇔ex2+2y2−xy+(x2−xy+2y2)=e1+y2+(1+y2)e^{x^{2} + 2 y^{2}} + e^{x y} \left( x^{2} - x y + y^{2} - 1 \right) - e^{1 + x y + y^{2}} = 0 \\ \Leftrightarrow e^{x^{2} + 2 y^{2} - x y} + \left( x^{2} - x y + y^{2} - 1 \right) - e^{1 + y^{2}} = 0 \\ \Leftrightarrow e^{x^{2} + 2 y^{2} - x y} + \left( x^{2} - x y + 2 y^{2} \right) - \left( 1 + y^{2} \right) - e^{1 + y^{2}} = 0 \\ \Leftrightarrow e^{x^{2} + 2 y^{2} - x y} + \left( x^{2} - x y + 2 y^{2} \right) = e^{1 + y^{2}} + \left( 1 + y^{2} \right)
Xét hàm số f(t)=et+tf \left( t \right) = e^{t} + t đồng biến trên R\mathbb{R}
f[x2−xy+2y2]=f(1+y2)⇒x2−xy+2y2=1+y2f \left[\right. x^{2} - x y + 2 y^{2} \left]\right. = f \left( 1 + y^{2} \right) \Rightarrow x^{2} - x y + 2 y^{2} = 1 + y^{2}
⇔x2−xy+y2=1⇔(x+y)2−3xy=1\Leftrightarrow x^{2} - x y + y^{2} = 1 \Leftrightarrow \left( x + y \right)^{2} - 3 x y = 1
Đặt u=x+y⇒xy=u2−13u = x + y \Rightarrow x y = \dfrac{u^{2} - 1}{3}
Ta có (x+y)2≥4xy⇒u2≥4.u2−13⇒−2≤u≤2\left( x + y \right)^{2} \geq 4 x y \Rightarrow u^{2} \geq 4 . \dfrac{u^{2} - 1}{3} \Rightarrow - 2 \leq u \leq 2
Do đó P=11+xy=11+u2−13=3u2+2P = \dfrac{1}{1 + x y} = \dfrac{1}{1 + \dfrac{u^{2} - 1}{3}} = \dfrac{3}{u^{2} + 2}
Xét hàm số f(u)=3u2+2⇒f′(u)=−6u(u2+2)2f \left( u \right) = \dfrac{3}{u^{2} + 2} \Rightarrow f^{'} \left( u \right) = \dfrac{- 6 u}{\left( u^{2} + 2 \right)^{2}}
f′(u)=0⇔u=0f^{'} \left( u \right) = 0 \Leftrightarrow u = 0
Bảng biến thiên :



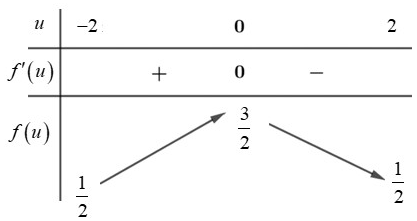
Từ bảng biến thiên ta được .

Câu hỏi tương tự:

#8556 THPT Quốc giaToán

Cho các số thực x; yx ; \textrm{ } y thỏa mãn ex2+2y2+exy(x2−xy+y2−1)−e1+xy+y2=0e^{x^{2} + 2 y^{2}} + e^{x y} \left( x^{2} - x y + y^{2} - 1 \right) - e^{1 + x y + y^{2}} = 0. Gọi M, mM , \textrm{ } m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P=11+xyP = \dfrac{1}{1 + x y}. Tính M−mM - m:

Lượt xem: 145,465 Cập nhật lúc: 20:08 02/08/2024

#8274 THPT Quốc giaToán

Cho các số thực x,yx , y thỏa mãn ex2+2y2+exy(x2−xy+y2−1)−e1+xy+y2=0e^{x^{2} + 2 y^{2}} + e^{x y} \left( x^{2} - x y + y^{2} - 1 \right) - e^{1 + x y + y^{2}} = 0. Gọi M,mM , m lần
lượt là GTLN, GTNN của biểu thức P=11+xyP = \dfrac{1}{1 + x y}. Tính M−mM - m.

Lượt xem: 140,680 Cập nhật lúc: 22:34 02/08/2024

#7972 THPT Quốc giaToán

Gọi SS là tập hợp các số phức z=a+bi (a,b∈R)z = a + b i \textrm{ } \left( a , b \in \mathbb{R} \right) thỏa mãn và ab≤0.a b \leq 0 . Xét z1z_{1} và z2z_{2} thuộc SS sao cho z1−z2−1+i\dfrac{z_{1} - z_{2}}{- 1 + i} là số thực dương. Giá trị nhỏ nhất của biểu thức ∣z1+3i∣+∣z2∣\left|\right. z_{1} + 3 i \left|\right. + \left|\right. z_{2} \left|\right. bằng

Lượt xem: 135,542 Cập nhật lúc: 16:26 04/08/2024

#8473 THPT Quốc giaToán

Gọi SS là tập hợp các số phức z=a+bi  (a, b∈R)z = a + b i \textrm{ }\textrm{ } \left( a , \textrm{ } b \in R \right) thỏa mãn và ab≤0a b \leq 0. Xét z1z_{1} và z2z_{2} thuộc SS sao cho z1−z2−1+i\dfrac{z_{1} - z_{2}}{- 1 + i} là số thực dương. Giá trị nhỏ nhất của biểu thức ∣z1∣+∣z2−i∣\left|\right. z_{1} \left|\right. + \left|\right. z_{2} - i \left|\right. bằng

Lượt xem: 144,074 Cập nhật lúc: 23:41 31/07/2024

#8636 THPT Quốc giaToán

Gọi SS là tập hợp tất cả các số phức zz thoả mãn điều kiện z.zˉ=∣z+zˉ∣z . \bar{z} = \left|\right. z + \bar{z} \left|\right.. Xét các số phức z1,z2∈Sz_{1} , z_{2} \in Ssao cho ∣z1−z2∣=1\left|\right. z_{1} - z_{2} \left|\right. = 1. Giá trị nhỏ nhất của biểu thức P=∣z1−3i∣+∣(zˉ)2+3i∣P = \left|\right. z_{1} - \sqrt{3} i \left|\right. + \left|\right. \left(\bar{z}\right)_{2} + \sqrt{3} i \left|\right. bằng

Lượt xem: 146,832 Cập nhật lúc: 16:25 04/08/2024

#8335 THPT Quốc giaToán

Cho các số thực x,yx , y thỏa mãn x.x5.(e)2x+2y5≥25(e)x+y+35x2x . \sqrt[5]{x} . \left(\text{e}\right)^{\dfrac{2 x + 2 y}{5}} \geq \dfrac{2}{5} \left(\text{e}\right)^{x + y} + \dfrac{3}{5} x^{2}. Giá trị nhỏ nhất của biểu thức P=3x2−yP = 3 x^{2} - y là

Lượt xem: 141,705 Cập nhật lúc: 21:21 02/08/2024

#8495 THPT Quốc giaToán

Cho

,

là các số thực dương thỏa mãn

. Tìm giá trị nhỏ nhất của biểu thức

.

Lượt xem: 144,439 Cập nhật lúc: 17:28 04/08/2024

#8675 THPT Quốc giaToán

Cho hai số phức  z1,z2z_{1}, z_{2} thỏa mãn  ∣z1+3+2i∣=1\left| z_{1} + 3 + 2i \right| = 1 và  ∣z2+2−i∣=1\left| z_{2} + 2 - i \right| = 1. Xét các số phức  z=a+bi, (a,b∈R)z = a + bi, \textrm{ } (a, b \in \mathbb{R}) thỏa mãn  2a−b=02a - b = 0. Khi biểu thức  T=∣z−z1∣+∣z−2z2∣T = \left| z - z_{1} \right| + \left| z - 2z_{2} \right| đạt giá trị nhỏ nhất thì giá trị biểu thức  P=3a2−b3P = 3a^{2} - b^{3} bằng

Lượt xem: 147,531 Cập nhật lúc: 12:22 29/07/2024

#11283 THPT Quốc giaHoá học

Thủy phân hoàn toàn chất hữu cơ E (C9H16O4, chứa 2 chức este) bằng dung dịch NaOH, thu được sản phẩm gồm ancol X và hai chất hữu cơ Y, Z. Biết Y chứa 3 nguyên tử C và MX < MY > MZ. Cho Z tác dụng với dung dịch HCl loãng, dư thu được hợp chất hữu cơ T (C3H6O3). Cho các phát biểu sau:

a. Cho a mol T tác dụng với một lượng dư Na thu được a mol H2;

b. Có 4 công thức cấu tạo thõa mãn tính chất của E;

c. Ancol X là propan-1,2-điol;

d. Khối lượng mol của Z là 96 g/mol.

Số lượng phát biểu đúng là

Lượt xem: 191,838 Cập nhật lúc: 15:22 19/08/2024


Đề thi chứa câu hỏi này:

86. Đề thi thử TN THPT môn Toán năm 2024 - CỤM SỞ HẢI DƯƠNG - LẦN 2THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,097 lượt xem 2,184 lượt làm bài