Gọi
là tập hợp các số phức
thỏa mãn
\textrm{ } \left| z + \bar{z} \left|\right. + \left|\right. z - \bar{z} \left|\right. = 2 và
. Xét
và
thuộc
sao cho
là số thực dương. Giá trị nhỏ nhất của biểu thức
bằng
A.
.
B.
.
C. 1.
D.
.
Đáp án đúng là: A
Gọi là tập hợp các số phức thỏa mãn \textrm{ } \left| z + \bar{z} \left|\right. + \left|\right. z - \bar{z} \left|\right. = 2 và . Xét và thuộc sao cho là số thực dương. Giá trị nhỏ nhất của biểu thức bằng
.
.
1.
.
Đáp án đúng là: A
.
(Vì
nên
trái đấu).
Gọi M là điểm biểu diễn của
, N là điểm biểu diễn của
.
Ta có:
là số thực dương
.
cùng hướng với
(với A là điểm biểu diễn của
).
.
Mà:
.
Ta có:
.
.
.
.
Bảng biến thiên
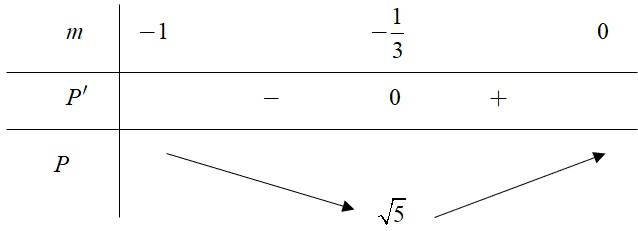
Suy ra, chọn đáp án A
Câu hỏi tương tự:
#7972 THPT Quốc giaToán
Gọi là tập hợp các số phức thỏa mãn và Xét và thuộc sao cho là số thực dương. Giá trị nhỏ nhất của biểu thức bằng
Lượt xem: 135,635 Cập nhật lúc: 16:14 13/05/2025
#8636 THPT Quốc giaToán
Gọi là tập hợp tất cả các số phức thoả mãn điều kiện . Xét các số phức sao cho . Giá trị nhỏ nhất của biểu thức bằng
Lượt xem: 146,924 Cập nhật lúc: 08:31 13/05/2025
#7779 THPT Quốc giaToán
Cho số phức thoả mãn . Gọi là tập hợp tất cả các số phức . Xét các số phức thỏa mãn , giá trị lớn nhất của bằng.
Lượt xem: 132,356 Cập nhật lúc: 21:40 12/05/2025
#8985 THPT Quốc giaToán
Cho là tập hợp các số phức thỏa . Gọi , là hai số phức thuộc tập hợp sao cho . Tính giá trị của biểu thức .
Lượt xem: 152,915 Cập nhật lúc: 10:42 16/05/2025
#8644 THPT Quốc giaToán
Gọi là tập hợp các số tự nhiên có ba chữ số đôi một khác nhau được lập thành từ các chữ số . Cho ngẫu nhiên một số từ , tính xác suất để số được chọn là một số chia hết cho .
Lượt xem: 147,073 Cập nhật lúc: 02:44 17/05/2025
#8185 THPT Quốc giaToán
Gọi là tập hợp các số tự nhiên có chữ số khác nhau được lập từ . Chon ngẫu nhiên một số từ tập . Xác suất để số được chon là một số chẵn bằng
Lượt xem: 139,244 Cập nhật lúc: 17:25 16/05/2025
#8151 THPT Quốc giaToán
Gọi là tập hợp tất các số tự nhiên có ít nhất chữ số và các chữ số đôi một khác nhau được lập từ các chữ số Chọn ngẫu nhiên hai số từ . Xác suất để hai số chọn được đều là số có ba chữ số là
Lượt xem: 138,673 Cập nhật lúc: 23:57 16/05/2025
#8594 THPT Quốc giaToán
Gọi là tập hợp các giá trị của tham số để giá trị lớn nhất của hàm số trên đoạn bằng . Tính tổng tất cả các phần tử của
Lượt xem: 146,259 Cập nhật lúc: 04:13 17/05/2025
#8031 THPT Quốc giaToán
Gọi là tập hợp các giá trị nguyên của tham số để hàm số đồng biến trên khoảng Tổng tất cả các phần tử của tập bằng
Lượt xem: 136,687 Cập nhật lúc: 14:22 14/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
5,446 xem403 thi
