Có bao nhiêu giá trị nguyên của tham số $m \in \left[\right. - 2023 ; \textrm{ } 2023 \left]\right.$ để bất phương trình $\left( 5 + \sqrt{21} \right)^{x} + \left( 6 - m \right) \left( 5 - \sqrt{21} \right)^{x} - \left( m + 2 \right) 2^{x} \geq 0$ nghiệm đúng với $\forall x \in \mathbb{R}$?

A.  

$2020$.

B.  

$2023$.

C.  

$2022$.

D.  

$2026$.

Đáp án đúng là: D

(NB):
Phương pháp:
Hàm đặc trưng.
Cách giải:
$\left( 5 + \sqrt{21} \left(\right)\right)^{x} + \left( 6 - m \right) \left( 5 - \sqrt{21} \left(\right)\right)^{x} - \left( m + 2 \right) 2^{x} \geq 0$
$\left( \dfrac{5 + \sqrt{21}}{2} \right)^{x} + \left( 6 - m \right) \left( \dfrac{5 - \sqrt{21}}{2} \right)^{x} \geq \left( m + 2 \right)$
Đặt $t = \left( \dfrac{5 + \sqrt{21}}{2} \right)^{x} > 0 , \left( \dfrac{5 - \sqrt{21}}{2} \right)^{x} = \dfrac{1}{t}$. Bất phương trình đã cho trở thành:
$t + \left( 6 - m \right) . \dfrac{1}{t} \geq m + 2 \Leftrightarrow \dfrac{t^{2} - 2 t + 6}{t + 1} \geq m$.
Xét hàm số $f \left( t \right) = \dfrac{t^{2} - 2 t + 6}{t + 1}$ trên khoảng $\left( 0 ; + \infty \right)$, ta có $f^{'} \left( t \right) = \dfrac{t^{2} + 2 t - 8}{\left( t + 1 \left(\right)\right)^{2}}$
$f^{'} \left( t \right) = 0 \Leftrightarrow \left[\right. t = - 4 \\ t = 2$. Khi đó, ta có bảng biến thiên sau:

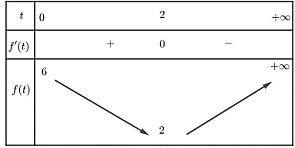
Từ bảng biến thiên trên ta suy ra để bất phương trình đã cho nghiệm đúng với $\forall x \in \mathbb{R}$ thì $m \leq 2$. Suy ra trong đoạn [-2023;2023] có tất cả 2026 giá trị nguyên của $m$ thỏa mãn yêu cầu bài toán.