Cắt khối hộp $A B C D . A^{'} B^{'} C^{'} D^{'}$ bởi các mặt phẳng $\left( A B^{'} D^{'} \right)$, $\left( C B^{'} D^{'} \right)$, $\left( B^{'} A C \right)$, $\textrm{ } \left( D^{'} A C \right)$ (hình minh họa) ta được khối đa diện có thể tích lớn nhất là

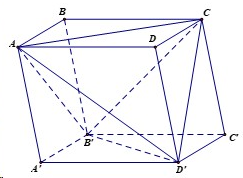
A.  

$A C B^{'} D^{'}$

B.  

$A^{'} C^{'} B D$

C.  

$A^{'} C B^{'} D^{'}$

D.  

$A C^{'} B^{'} D^{'}$.

Đáp án đúng là: A

Cho hai mặt phẳng $\left( P \right)$và $\left( Q \right)$ song song với nhau và cùng cắt khối cầu tâm $O$ bán kính $4 \sqrt{3}$ thành hai hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách $h$ giữa hai mặt phẳng $\left( P \right)$và $\left( Q \right)$ bằng:

Một mạch dao động LC gồm tụ điện $C$ có điện dung $200\mu \mathrm{F}$, cuộn dây có hệ số tự cảm $L=\mathrm{0,2}\mathrm{H}$ và điện trở là $R_0=4\mathrm{\Omega }$ và điện trở của dây nối $R=20\mathrm{\Omega }$. Dùng dây nối có điện trở không đáng kể để nối hai cực của nguồn điện một chiều có suất điện động $E=12\mathrm{V}$ và điện trở trong $\mathrm{r}=1\mathrm{\Omega }$ với hai bản cực của tụ điện. Sau khi trạng thái trong mạch đã ổn định người ta cắt nguồn ra khỏi mạch để cho mạch dao động tự do. Tính nhiệt lượng tỏa ra trên R kể từ lúc cắt nguồn ra khỏi mạch đến khi dao động trong mạch tắt hoàn toàn?

Cho khối trụ có hai đáy lần lượt là hình tròn tâm $O , O^{'}$ và chiều cao bằng $\sqrt{2} a$. Một mặt phẳng đi qua tâm $O$, tạo với $O O^{'}$ một góc $\left(30\right)^{@}$ đồng thời cắt hai đường tròn tâm $O , O^{'}$ tại bốn điểm tạo thành bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng $2 a^{2}$. Thể tích của khối trụ đã cho bằng