Cho hai đường tròn
và
cắt nhau tại hai điểm
sao cho
là một đường kính của đường tròn
. Gọi
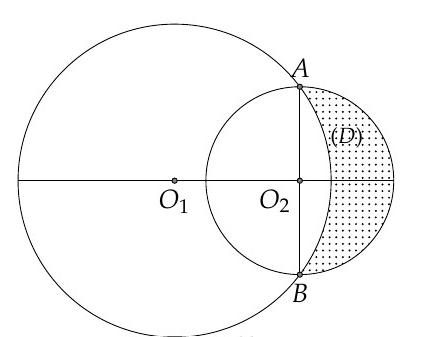
là phần hình phẳng giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần tô dấu chấm như hình vẽ). Quay
quanh trục
ta được một khối tròn xoay. Tính thể tích
của khối tròn xoay được tạo thành.
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: B
Cho hai đường tròn
và
cắt nhau tại hai điểm
sao cho
là một đường kính của đường tròn
. Gọi
là phần hình phẳng giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần tô dấu chấm như hình vẽ). Quay
quanh trục
ta được một khối tròn xoay. Tính thể tích
của khối tròn xoay được tạo thành.

.
.
.
.
Đáp án đúng là: B
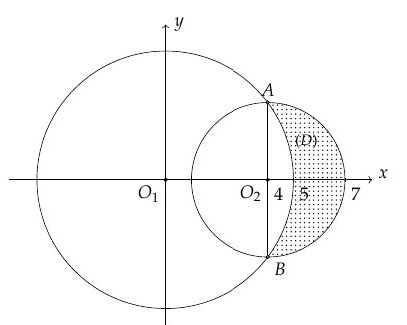
Chọn hệ tọa độ như hình vẽ sao cho trùng gốc tọa độ. Khi đó và .
Khi đó .
Câu hỏi tương tự:
#8635 THPT Quốc giaToán
Cho hình trụ có hai đáy là hình tròn tâm và , chiều cao . Mặt phẳng đi qua tâm và tạo với một góc , cắt hai đường tròn tâm và tại bốn điểm là bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng . Thể tích của khối trụ được giới hạn bởi hình trụ đã cho bằng
Lượt xem: 146,954 Cập nhật lúc: 14:18 02/05/2025
#8353 THPT Quốc giaToán
Cho khối trụ có hai đáy lần lượt là hình tròn tâm và chiều cao bằng . Một mặt phẳng đi qua tâm , tạo với một góc đồng thời cắt hai đường tròn tâm tại bốn điểm tạo thành bốn đỉnh của một hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng . Thể tích của khối trụ đã cho bằng
Lượt xem: 142,106 Cập nhật lúc: 18:33 01/05/2025
#8387 THPT Quốc giaToán
Cho hình trụ có hai đáy là hai hình tròn và , chiều cao . Một mặt phẳng đi qua trung điểm của và tạo với một góc . Mặt phẳng cắt đường tròn đáy tại hai điểm . Tính độ dài đoạn thẳng theo ?
Lượt xem: 142,690 Cập nhật lúc: 07:04 03/05/2025
#7543 THPT Quốc giaToán
Trong mặt phẳng cho hai điểm và Đường tròn tâm và đi qua điểm có phương trình là
Lượt xem: 128,374 Cập nhật lúc: 17:11 30/04/2025
#8426 THPT Quốc giaToán
Cho hình trụ có hai đáy là hai hình tròn và , thiết diện qua trục của hình trụ là hình vuông. Gọi và là hai điểm lần lượt nằm trên hai đường tròn và . Biết và khoảng cách giữa và bằng . Bán kính đáy của hình trụ bằng
Lượt xem: 143,346 Cập nhật lúc: 02:11 03/05/2025
#11393 THPT Quốc giaToán
Cho hình trụ có hai đáy là hai hình tròn và , thiết diện qua trục của hình trụ là hình vuông. Gọi và là hai điểm lần lượt nằm trên hai đường tròn và . Biết và khoảng cách giữa và bằng . Tính diện tích xung quanh của hình trụ.
Lượt xem: 193,755 Cập nhật lúc: 08:01 27/04/2025
#8740 THPT Quốc giaToán
Cho hình trụ có tâm hai đường tròn đáy lần lượt là và , bán kính đáy hình trụ bằng . Trên đường tròn đáy và lần lượt lấy hai điểm sao cho tạo với trục của hình trụ một góc và có khoảng cách đến trục của hình trụ bằng . Tính thể tíc khối chóp
Lượt xem: 148,657 Cập nhật lúc: 19:24 02/05/2025
#8555 THPT Quốc giaToán
Cho hình trụ có hai đáy là hai hình tròn và ; là một dây cung của đường tròn sao cho tam giác đều và mặt phẳng tạo với mặt phẳng chứa đường tròn một góc . Tính thể tích của hình trụ đã cho.
Lượt xem: 145,540 Cập nhật lúc: 17:13 30/04/2025
#8808 THPT Quốc giaToán
Cho mặt cầu có bán kính bằng 4, hình trụ có chiều cao bằng 4 và hai đường tròn đáy nằm trên . Gọi là thể tích khối trụ và là thể tích của khối cầu . Tỉ số bằng
Lượt xem: 149,896 Cập nhật lúc: 15:16 03/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
4,739 xem355 thi
