Cho hàm số $y = f \left( x \right)$. Đồ thị hàm số $y = f^{'} \left( x \right)$ như hình vẽ bên dưới và $f \left( - 2 \right) = f \left( 2 \right) = 0$.

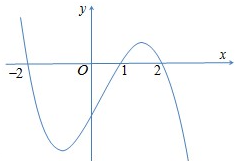
Hàm số $g \left( x \right) = \left(\left[\right. f \left( x \right) \left]\right.\right)^{2}$ đồng biến trên khoảng nào trong các khoảng sau?

A.  

$\left( - 4 ; - 3 \right)$.

B.  

$\left( 2 ; 4 \right)$.

C.  

$\left( 0 ; 2 \right)$.

D.  

$\left( - 3 ; 1 \right)$.

Đáp án đúng là: C

Cho hàm số $f \left( x \right)$ liên tục trên $\mathbb{R}$ có đồ thị như hình vẽ

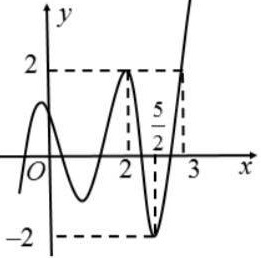
Có bao nhiêu giá trị nguyên dương nhỏ hơn $10$ của tham số $m$ để phương trình $f \left( 2^{x} + 2^{- x} \right) = f \left( 2^{m} + 2^{- m} \right)$ có $2$ nghiệm phân biệt?
A. $6$. B. $7$. C. $9$. D. $4$.
Lời giải
Đặt $2^{x} + 2^{- x} = t$. Ta có phương trình $f \left( t \right) = f \left( 2^{m} + 2^{- m} \right)$
Do $2^{x} + 2^{- x} \geq 2$ nên $t \geq 2$.
Ứng với mỗi giá trị của $t < 2$ thì phương trình $2^{x} + 2^{- x} = t$ vô nghiệm.
Ứng với mỗi giá trị của $t = 2$ thì phương trình $2^{x} + 2^{- x} = t$ có đúng một nghiệm.
Ứng với mỗi giá trị của $t > 2$ thì phương trình $2^{x} + 2^{- x} = t$ có hai nghiệm phân biệt.
Phương trình $f \left( 2^{x} + 2^{- x} \right) = f \left( 2^{m} + 2^{- m} \right)$có hai nghiệm phân biệt khi phương trình $f \left( t \right) = f \left( 2^{m} + 2^{- m} \right)$ có đúng một nghiệm $t > 2$.
Từ đồ thị hàm số $y = f \left( x \right)$ ta có phương trình $f \left( t \right) = f \left( 2^{m} + 2^{- m} \right)$ có đúng một nghiệm $t > 2$ khi $\left[\right. f \left( 2^{m} + 2^{- m} \right) = - 2 \\ f \left( 2^{m} + 2^{- m} \right) > 2 \Leftrightarrow \left[\right. 2^{m} + 2^{- m} = \dfrac{5}{2} \\ 2^{m} + 2^{- m} > 3 \Leftrightarrow \left[\right. 2^{2 m} - \dfrac{5}{2} . 2^{m} + 1 = 0 \text{ } \left( 1 \right) \\ 2^{2 m} - 3 . 2^{m} + 1 > 0 \text{ } \left( 2 \right)$.
Xét phương trình $2^{2 m} - \dfrac{5}{2} . 2^{m} + 1 = 0 \Leftrightarrow \left[ 2^{m} = 2 \\ 2^{m} = \dfrac{1}{2} \Leftrightarrow \left[\right. m = 1 \\ m = - 1$.
Xét bất phương trình $2^{2 m} - 3 . 2^{m} + 1 > 0 \Leftrightarrow \left[\right. 2^{m} > \dfrac{3 + \sqrt{5}}{2} \\ 2^{m} < \dfrac{3 - \sqrt{5}}{2} \Leftrightarrow \left[\right. m > \left(log\right)_{2} \left(\right. \dfrac{3 + \sqrt{5}}{2} \right) \\ m < \left(log\right)_{2} \left( \dfrac{3 - \sqrt{5}}{2} \right)$.
Do $m$ là số nguyên dương nhỏ hơn $10$ nên $m \in \left{ 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 \right}$ $\Rightarrow$có $9$ giá trị của $m$.